Opracowanie wyników

1. obliczenie Δm

Nr. kolby	Masa pustej kolby [g]	Masa kolby z roztworem [g]	Δm [g]
1	133,60	183,23	49,63
2	128,95	178,43	49,48
3	108,36	133,06	24,70
4	128,00	152,69	24,69

2. obliczanie gęstości roztworów ze wzoru
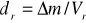
   , gdzie Δm - różnica mas kolby z nasyconym roztworem kwasu benzoesowego i kolby pustej, V_r - objętość kwasu przed miareczkowaniem np.

d₁=

Analogiczne obliczenia stosujemy dla pozostałych roztworów:

Nr. kolby	Δm [g]	Vr [cm^3]	dr [g/cm^3]
1	49,63	50	0,9326
2	49,48	50	0,9896
3	24,70	25	0,9880
4	24,69	25	0,9876

3. obliczanie stężenia molowego kwasu benzoesowego z zależności:

gdzie V_kwasu - objętość roztworu przed miareczkowaniem, c_kwasu - stężenie molowe kwasu benzoesowego w roztworze, V_NaOH - objętość mianowanego roztworu NaOH użyta podczas miareczkowania, c_NaOH - stężenie mianowanego roztworu NaOH (0,1003 mol/dm³)

Nr. Kolby	VNaOH [cm^3]	cNaOH [mol/dm^3]	Vkwasu [cm^3]	ckwasu [mol/dm^3]
1	16,9	0,1003	50	0,0339
2	17,0	0,1003	50	0,0341
3	11,6	0,1003	25	0,0465
4	11,1	0,1003	25	0,0445

• Kolba 1
  

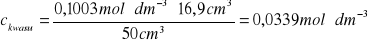
• Kolba 2
  

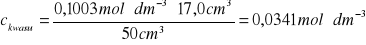
• Kolba 3
  

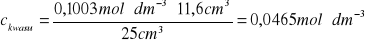
• Kolba 4
  

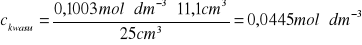
d) obliczenie rozpuszczalności z zależności:

K=

, gdzie: c_r - stężenie molowe wyznaczone metodą miareczkowania alkacymetrycznego roztworu nasyconego w danej temperaturze [mol/dm³], M_s - masa molowa substancji (dla kwasu benzoesowego = 122,12 g/mol), d_r - gęstość roztworu nasyconego danej substancji [g/dm³].

Nr. Kolby	cr [mol/dm^3]	dr [g/dm^3]	Rs [g/100 cm^3 H2O]
1	0,0339	932,6	0,4454
2	0,0341	989,6	0,4222
3	0,0465	988,0	0,5663
4	0,0445	987,6	0,5528

• Kolba numer 1-
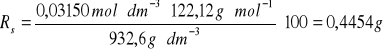
  /100 g H₂O

• Kolba numer 2-
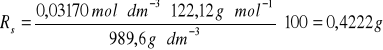
  /100 g H₂O

• Kolba numer 3-
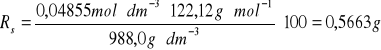
  /100 g H₂O

• Kolba numer 4-
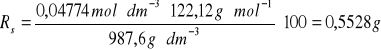
  /100 g H₂O

e) wyznaczenie entalpii procesu rozpuszczania,

T₁ K₁ =

K
=

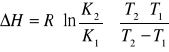
, gdzie: K₂ i K₁ - rozpuszczalność substancji w temperaturach T₂ i T₁, R - stała gazowa [
], T₁ - 300,15K, T₂ - 313,15K. Podstawiając dane do wzoru otrzymujemy:

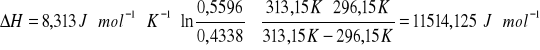
Wartość średnia ΔH wynosi 11514,125 J/mol=11,514 kJ/mol

Wyznaczanie entalpii rozpuszczania biorąc pod uwagę kąt nachylenia prostej:

Równanie prostej opisującej wykres dane jest wzorem: y= -1601,42x +5,77

a= - 1601,42 K

Następnie sporządzamy wykres zależności stałej równowagi. Wykorzystując wartość tg α odczytaną z funkcji wykresu, można obliczyć entalpię rozpuszczania ze wzoru:

ΔH=24,6032 kJ/mol

5.Wnioski

Entalpia rozpuszczania kwasu benzoesowego jest reakcją endotermiczną, czego dowodzi wykres. Rozpuszczalność kwasu rośnie wraz ze wzrostem temperatury. Porównując metodę algebraiczną z teoretyczną , uzyskujemy zbliżone wyniki, co dowodzi słuszności zastosowanej metody. Wartości na wykresie dla obydwu wartości lnK₂ nieco odbiegają od siebie w porównaniu do lnK₁, czego przyczyna mogły być błędy pomiarowe- szczególnie dużą różnicą w stężeniach molowych obydwu roztworów, gdyż roztwór ten miał wyższą temperaturę. Mogło to spowodować błędy podczas miareczkowania , na co wpływ miało ochłodzenie się roztworu i wytrącenie części kwasu.

---