Rachunek prawdopodobieństwa i statystyka matematyczna
Zb zdarzeń elementarnych, ciało zdarzeń, definicja aksjomatyczna prawdopodobieństwa.
Określenie i własności dystrybuanty własności dystrybuanty rozkładu prawdopodobieństwa..
Sprawdzić, czy funkcja
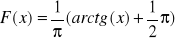
może być dystrybuantą rozkładu prawdopodobieństwa.
Definicja prawdopodobieństwa warunkowego, udowodnić, że prawdopodobieństwo warunkowe spełnia aksjomaty definicji prawdopodobieństwa.
Udowodnić, że
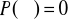
.Udowodnić, że
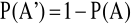
Udowodnić, że dla dowolnych dwóch zdarzeń
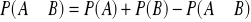
.Udowodnić, że: jeśli
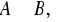
to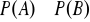
.Wykazać, że dla każdego zdarzenia A
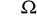
, gdzie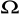
oznacza zdarzenie pewne zachodzi nierówność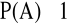
.Sformułować i udowodnić twierdzenie o prawdopodobieństwie zupełnym.
Sformułować i udowodnić twierdzenie Bayesa.
Definicja zmiennej losowej.
Udowodnić, że
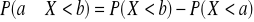
.Zmienne losowe typu skokowego. Rozkład zmiennej losowej typu skokowego.
Zmienne losowe typu ciągłego. Rozkład zmiennej losowej typu ciągłego.
Rozkład Bernoulliego
Rozkład Poissona
Sformułować i udowodnić twierdzenie Poissona.
Rozkład normalny.
19.Napisać funkcję gęstości zmiennej losowej o rozkładzie normalnym z wartością oczekiwaną 5 i odchyleniem standardowym 7.
20. Zmienna losowa X ma rozkład N(3,5) napisać jej funkcję gęstości.
Parametry zmiennych losowych (średnia, wariancja, odchylenie standardowe, mediana i wartość modalna).
Udowodnić, że jeśli zmienna losowa X ma wartość oczekiwaną m i odchylenie standardowe σ, to zmienna losowa
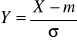
ma wartość oczekiwaną zero i odchylenie standardowe 1.Udowodnić, że jeśli zmienna losowa X ma wartość oczekiwaną 5 i odchylenie standardowe 3, to zmienna losowa
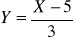
ma wartość oczekiwaną zero i odchylenie standardowe 1.
Twierdzenie Linderberga-Levy'ego
Określenie populacji i próby
Definicja i własności estymatorów punktowych
Wyprowadzić wzór na estymator wartości oczekiwanej
Udowodnić, że średnia arytmetyczna jest nieobciążonym estymatorem wartości oczekiwanej.
Udowodnić, że
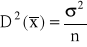
Wyprowadzić wzór na przedział ufności dla wartości oczekiwanej na podstawie próby z populacji o rozkładzie normalnym ze znanym odchyleniem standardowym.
Omówić metodę najmniejszych kwadratów na wybranym przykładzie.
Wyszukiwarka
Podobne podstrony:
rozklad chi2 t Studenta, ISI UWM, Semestr III, Metody probabilistyczne
Rozklad Poissona 1, ISI UWM, Semestr III, Metody probabilistyczne
Zagadnienia na egzamin z Gutka, ZUT-Energetyka-inżynier, III Semestr, Wytrzymałość materiałów II, Wy
Zagadnienia na egzamin końcowy po pierwszym semestrze
Zagadnienia na egzamin z EGiB. 2011, Studia, 4 semestr, EGiB, egzamin
zagadnienia na egzamin od dr Rutkiewicza[1]. , semestr 2, ochrona
zagadnienia na egzamin ustny, materiały- polonistyka, część III
Przykładowe-pytania-i-zagadnienia-na-egzamin-z-kultur-tk.-2013 (1), Semestr VI, Kultury tkankowe i k
Zagadnienia na egzamin 2014, Inżynieria Materiałowa, Semestr 6, Sesja
zagadnienia na egzamin dyplomowy, Pedagogika materiały, Semestr V
ZAGADNIENIA NA EGZAMIN Z MECHANIKI TECHNICZNEJ II DLA SEMESTRU III, sem III, +Mechanika Techniczna I
zagadnienia na egzamin, UWM Gospodarka Przestrzenna PiIP, semestr IV, Kataster Nieruchomości
Zagadnienia na egzamin z wiedzy o historycznym rozwoju polszczyzny, Filologia polska, ROK III, semes
metodologia - zagadneinia na egzamin, UKSW - Pedagogika, II rok - I semestr, Metodologia Badań Pedag
7 wersologia 2, Filologia polska UWM, Teoria literatury, zagadnienia na egzamin
9 GENOLOGIA, Filologia polska UWM, Teoria literatury, zagadnienia na egzamin
ZAGADNIENIA NA EGZAMIN Z METODYKI (1), metodyka nauczania języka polskiego, Egzamin z metodyki III r
13 garunki mieszane i pograniczne, Filologia polska UWM, Teoria literatury, zagadnienia na egzamin
więcej podobnych podstron