1. Cel ćwiczenia
Poznanie metod rozwiązywania obwodów elektrycznych oraz praktyczne pomiary prądów i napięć w rozgałęzionym obwodzie elektrycznym.
2.Obliczanie prostych obwodów elektrycznych
Rozwiązywaniem obwodów elektrycznych nazywamy znajdowanie rozpływu prądów i rozkładu napięć w poszczególnych gałęziach obwodów przy zadanych parametrach źródeł i odbiorników.
Jedną z najczęściej stosowanych metod obliczania obwodów jest metoda transfiguracji. Polega ona na przekształceniu obwodu w taki sposób, aby uzyskać możliwie prosty obwód, w którym obliczenie rozpływu prądów nie stwarza trudności. Następnie, wykorzystując prawo Ohma i prawa Kirchhoffa, powraca się do pierwotnej postaci obwodu i oblicza kolejno rozpływ prądów w jego poszczególnych gałęziach.
Metoda klasyczna rozwiązywania obwodów elektrycznych polega na zastosowaniu praw Kirchhoffa. Jeżeli liczba węzłów obwodu wynosi W, to liczba równań, które możemy ułożyć dla węzłów na podstawie I prawa Kirchhoffa, wynosi W-1. Pozostałe równania układamy dla oczek na podstawie II prawa Kirchhoffa, a liczba równań może być liczbie oczek obwodu. Metoda klasyczna pozwala teoretycznie na rozwiązanie dowolnego obwodu elektrycznego, chociaż przy dużej liczbie gałęzi i węzłów rozwiązywanie układu wielu równań może być trudne.
Metoda napięcia międzywęzłowego polega na obliczeniu napięcia między dwoma węzłami obwodu złożonego z kilku równoległych gałęzi, które składają się z rezystancji i sem. o znanych wartościach. Mając obliczone napięcie międzywęzłowe łatwo obliczyć prądy w poszczególnych gałęziach.
Metodą oczkowa polega na wyznaczeniu prądów oczkowych w poszczególnych oczkach obwodu.. W tym celu, na podstawie II prawa Kirchhoffa układa się równania dla oczek rozpatrywanego obwodu. Znając prądy oczkowe, można stosunkowo łatwo wyznaczyć prądy gałęziowe.
3. Prawo Ohma
Napięcie U mierzone na końcach przewodnika o rezystancji R (oporze elektrycznym) podczas przepływu prądu I jest równe iloczynowi rezystancji i prądu:
U = R I
![]()
- jednostka rezystancji
Jeden om jest rezystancją między dwoma punktami przewodu prostoliniowego, gdy niezmienna, różnica potencjałów równa jednemu woltowi, działająca między tymi dwoma punktami, wywołuje, w tym przewodzie przepływ prądu o natężeniu jednego ampera.
4. Prawa Kirchhoffa: prądowe: i napięciowe.
Prądowe prawo Kirchhoffa, zwane pierwszym prawem Kirchhoffa, można sformułować w sposób następujący: algebraiczna suma prądów w dowolnym węźle obwodu rozgałęzionego jest równa sen lub inaczej suną, prądów wpływających do węzła jest równa sumie prądów odpływających od węzła. Prawu temu odpowiada równanie o postaci:
![]()
przy czym I, oznacza prąd w gałęzi k-tej przyłączonej do danego węzła obwodu:
Rys. 1
Przykładowo w węźle przedstawionym na rys.1
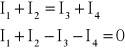
Znak plus przypisujemy prądom o zwrocie do węzła (dopływającym), a znak minus prądom o zwrocie od węzła (odpływającym).
Napięciowe prawo Kirchhoffa, zwane również drugim prawem Kirchhoffa brzmi następująco: w dowolnym oczku obwodu elektrycznego suma algebraiczna napięć źródłowych i napięć odbiornikowych jest równa zeru. Prawu temu odpowiada równanie o postaci:
![]()
gdzie: Uk - napięciowe odbiornikowe k-tej gałęzi danego oczka,
Ek - napięcie źródła napięciowego w k-tej gałęzi danego oczka.
5.Schemat pomiarowy:
I1=0,5A U1=2,26V
I2=0,33A U2=27,2V
I3=0,17A U3=27,2V
Rz
![]()
Ω
![]()
![]()
![]()
Znak plus nadajemy napięciom, których zwrot jest zgodny z dodatnim obiegiem oczka, a znak minus nadajemy napięciom o zwrocie przeciwnym. Na podstawie praw Kirchhoffa i prawa Ohma można wyznaczyć odpowiedź obwodu (prąd lub na danym elemencie obwodu) na znane wymuszenie (źródło prądowe lub napięciowe) i na odwrót wyznaczyć wymuszenie przy znanej odpowiedzi.
Wielkość |
Jednostka |
Wartość |
|
|
|
obliczona |
zmierzona |
I1 |
A |
0,509 |
0,5 |
I2 |
A |
0,339 |
0,33 |
I3 |
A |
0,17 |
0,17 |
U1 |
V |
2,29 |
2,26 |
U2 |
V |
26,4 |
27,2 |
U3 |
V |
27,2 |
27,2 |
6.Obliczenia błędów
![]()
![]()
ΔUz=29,50V-29,46V=0,04V
ΔU1=2,29V-2,26V=0,03V
ΔU2=26,40V-27,20V=-0,80V
ΔU3=27,20V-27,20V=0V
δ(Uzas)=(0,04V/29,46V)*100%=0,13%
δ(U1)=(0,03V/2,26V)*100%=1,33%
δ(U2)=(0,80V/27,20V)*100%=2,94%
δ(U3)=0 %
7.Wnioski
Analizując wyniki obliczeń wartości oraz zmierzonych wartości, można uznać, że są bardzo podobne. Niewielkie różnice wynikają z błędów, których nie uwzględniamy podczas pomiaru, np. oporność wewnętrzna miernika. Otrzymane wartości napięć podczas ćwiczenia za pomocą pomiaru miernikiem różnią się od obliczonych. Wartości te mogą być spowodowane pracą miernika. Natomiast wartości natężeń prądu są zbliżone do obliczonych co wskazuje na prawidłową pracę amperomierza w danym zakresie. Podczas obliczeń błędów pomiarowych można zauważyć, że wysoka dokładność pomiaru występuje w przypadku U3=0. Wartość błędu jest niewielka, jest to spowodowane bardzo dokładnym odczytem wartości z miernika. Niedokładności mogły również wynikać z zaokrągleń przy obliczeniach.
- 1 -
Wyszukiwarka
Podobne podstrony:
POMIARY PRĄDÓW I NAPIĘĆ W ROZGAŁZIONYM OBWODZIE ELEKTRYCZNYM
Pomiary prądów i napięć w rozgałęzionym obwodzie elektrycznym, Elektrotechnika, Instrukcje I
Pomiary pradow i napiec w rozgalezionym obwodzie elektrycznym
POMIARY PRĄDÓW I NAPIĘĆ W ROZGAŁZIONYM OBWODZIE ELEKTRYCZNYM
Pomiary prądów i napięć w rozgałęzionym obwodzie elektrycznym, Elektrotechnika, Instrukcje I
pomiar pradów i napieć w rozgałęzionym obwodzie elekt?
ściaga elaktr, UTP Transport, III sem, Elektrotechnika
Pomiary prądów i napięć, Spis przyrz˙d˙w do ˙wiczenia nr 3 ˙Pomiary pr˙d˙w i napi˙˙ sinusoidalnych i
Pomiar prądów i napięć za pomocą mierników analogowych, ANALOGOW, Pomiar pr˙d˙w i napi˙˙ za pomoc˙ m
Pomiar prądów i napięć okresowych doc
Pomiary wielkości elektrycznych Instrukcja do ćw 05 Badanie diody – charakterystyka prądowo napięc
Badanie przebiegow pradow i napiec sinusoidalnych w elementach RLC, UTP-ATR, Elektrotechnika i elekt
Metrologia - Pomiar współczynników tłumienia zakłóceń woltomierza cyfrowego napięcia stałego, Labora
Badanie ferrorezonansu prądów i napięć, Elektrotechnika- Ferrorezonans, II rok INFORMATYKA_
1224048119 Tabela pomiarowa do pomiaru pradu i napiecia, Laboratorium z podstaw elektrotechniki i el
1224048119 Tabela pomiarowa do pomiaru pradu i napiecia, Laboratorium z podstaw elektrotechniki i el
Badanie wytrzymałości powietrza przy napięciu przemiennym i pomiar wysokiego napięcia, Elektrotechni
głogowski,elektrotechnika, METODY POMIARU PRĄDOW
więcej podobnych podstron