Tematy 2006/2007
Elementy teorii błędów.
Oznaczenia : x,y,z, .... oraz *x, *y, *z, .... - wielkości przybliżone oraz oszacowania błędu bezwzględnego tych wielkości.
Wyjaśnić pojęcia związane z błędem: liczba przybliżona, błąd bezwzględny i błąd względny.
Wyprowadzić wzory na błąd bezwzględny i błąd względny wartości funkcji jednej i wielu zmiennych.
Wyprowadzić wzory na błąd bezwzględny i błąd względny działań arytmetycznych: sumy, różnicy, iloczynu i ilorazu.
Obliczyć błąd bezwzględny i błąd względny wartości funkcji f, gdy np. f(x) = xy2 oraz x =1, y =2 oraz *x=0.1, *y=0.05.
Obliczyć błąd bezwzględny i błąd względny objętości prostopadłościanu o bokach x=2 cm, y=3 cm i z=2 cm, jeżeli błąd przyrządu pomiarowego użytego do pomiarów boków wynosi 0.01 cm.
Wyjaśnić pojęcia: uwarunkowanie zadania numerycznego oraz wskaźnik uwarunkowania zadania numerycznego.
Podać wskaźnik uwarunkowania dla zadania obliczania wartości funkcji jednej zmiennej y = f(x). Obliczyć ten wskaźnik, gdy f(x) = exp(-x).
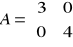
Podać wskaźnik uwarunkowania dla zadania rozwiązywania układu równań liniowych Ax = b. Obliczyć ten wskaźnik, gdy
Rozwiązywanie równań nieliniowych i ich układów.
Rozważamy zadanie znajdowania pierwiastków rzeczywistych
a) równania skalarnego f(x) = 0, a*x*b,
b) układu F(x) = 0.
2.1 Na czym polegają metody iteracyjne rozwiązywania rozważanego obecnie zadania numerycznego (dla
przypadku skalarnego). Zdefiniować wykładnik zbieżności takich metod. Podać ten wykładnik dla metody:
siecznych, stycznych, bisekcji.
2.2 Dla równania skalarnego, omówić metodę
a) siecznych, b) stycznych, c) bisekcji.
2.3 Podać założenia dotyczące
a) funkcji f, b) przedziału [a,b], c) punktów (punktu) startowych,
zapewniające zbieżność do pierwiastka ciągu generowanego przez metodę: siecznych, stycznych, bisekcji.
2.4 Wyznaczyć pierwsze przybliżenie:
np. w metodzie stycznych, gdy f(x) = 2x4-x2 i punkt startowy x0 = 1.
2.5 Czy można stosować metodę
np. stycznych, gdy f(x) = ex-x-1 i punkt startowy x0 = 0 ?
Interpolacja.
Funkcja przybliżana f zadana jest na zbiorze dyskretnym punktów {x0,x1, .... ,xn} - znane są jej wartości yi = f(xi) w punktach xi (i=0,1,....,n).
3.1 Sformułować zadanie interpolacyjne Lagrange'a.
3.2 Sformułować i udowodnić twierdzenie o jednoznaczności rozwiązania zadania interpolacyjnego Lagrange'a.
3.3 Podać wielomian interpolacyjny w postaci Lagrange'a dla funkcji f określonej następująco:
np. f(1) = 2, f(2) = 3, f(4) = 2.
3.4 Zdefiniować iloraz różnicowy 1-go rzędu, 2-go rzędu i ogólnie k-go rzędu.
Wyznaczyć tablicę ilorazów różnicowych dla funkcji f określonej następująco:
np. f(0) = 1, f(1) = 3, f(3) = 2.
3.5 Podać wielomian interpolacyjny w postaci Newtona dla funkcji f określonej następująco:
np. f(0) = 1, f(2) = 3, f(3) = 2.
3.6 Podać definicję funkcji sklejanej stopnia trzeciego.
3.7 Sformułować zadanie interpolacji przy pomocy funkcji sklejanych stopnia trzeciego. Czym są dodatkowe
warunki ?

3.8 Narysować bazę funkcji sklejanych stopnia trzeciego , gdy liczba węzłów równoodległych wynosi np. 7.
4. Aproksymacja średniokwadratowa dyskretna.
Funkcja przybliżana f zadana jest na zbiorze dyskretnym punktów {x0,x1, .... ,xn} - znane są jej wartości yi = f(xi) w punktach xi (i=0,1,....,n).
4.1 Sformułować zadanie aproksymacji średniokwadratowej dyskretnej.
Rozważyć przypadki aproksymacji typu wielomianowego i trygonometrycznego.
4.2 Wyprowadzić układ równań normalnych, gdy funkcja przybliżająca F jest postaci np.
F(x) = a0,
F(x) = a0+a1x,
F(x) = a0+a1x+a2x2,
F(x) = a0+a1sin(x)+a2cos(x).
4.3 Przyjmując, że G=MTM jest macierzą Grama, podać postać macierzy M., gdy np.
a) 2, x, x2, 2x są funkcjami bazowymi,
aproksymacji dokonujemy na zbiorze {-1,0,2,3}.
4.4 Omówić problem uwarunkowania zadania rozwiązywania układu równań normalnych.
5. Całkowanie numeryczne.
![]()
Rozważamy zadanie obliczania całki
gdzie p jest funkcją wagową.
5.1 Co to jest kwadratura ? Omówić rolę funkcji wagowej p.
5.2 Podać definicję rzędu kwadratury. Wykazać, że
np. kwadratura postaci S(f) = 2f(0), gdy a = -1, b = 1 oraz p(x) = 1, jest dokładna dla wielomianów
pierwszego stopnia.
5.3 Omówić prosty i złożony wzór trapezów.
5.4 Omówić prosty i złożony wzór parabol.
5.5 Omówić błąd złożonego wzoru trapezów i złożonego wzoru parabol.
5.6 Omówić 2 - punktową prostą i złożoną kwadraturę Gaussa-Legendre'a.
6. Rozwiązywanie zagadnień początkowych dla równań różniczkowych zwyczajnych.
6.1 Omówić metodę rozwijania rozwiązania w szereg potęgowy.
6.2. Omówić metody dyskretne. Wyjaśnić pojęcia: zbieżność i rząd metody dyskretnej.
6.3 Omówić jawną i niejawną metodę Eulera.
6.4 Dane jest zagadnienie początkowe y' = y + x, y(0) = 1. Za pomocą jawnej metody Eulera obliczyć y1 oraz
y2, gdy krok całkowania h = 0.1.
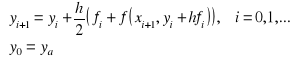
6.5 Dane jest zagadnienie początkowe y' = 2y + x, y(1) = 1 oraz metoda dyskretna (metoda Heuna rzędu 2-go)
gdzie fi = f(xi,yi). Obliczyć y1, gdy krok całkowania h = 0.2.
6.6 Wyznaczyć trzy pierwsze wyrazy rozwinięcia w szereg potęgowy rozwiązania y = y(x) zagadnienia
początkowego y ' = 3y2 +x, y(1) = 0.
![]()
![]()
Wyszukiwarka
Podobne podstrony:
metoda siecznych, Elektrotechnika, SEM3, Metody numeryczne, egzamin metody numeryczn
testMNłatwy0708, WI ZUT studia, Metody numeryczne, Metody Numeryczne - Ćwiczenia
metoda regula falsi, Elektrotechnika, SEM3, Metody numeryczne, egzamin metody numeryczn
Metody optymalizacji, Księgozbiór, Studia, Metody numeryczne
interpolacja, Elektrotechnika, SEM3, Metody numeryczne, egzamin metody numeryczn
symulacje numeryczne w pakiecie SCILAB SCICOS, Politechnika Lubelska, Studia, metody numeryczne
matoda stycznych newtona, Elektrotechnika, SEM3, Metody numeryczne, egzamin metody numeryczn
metoda prostokątów trapezów i simpsona, Elektrotechnika, SEM3, Metody numeryczne, egzamin metody num
więcej podobnych podstron