GEOMETRIA ANALITYCZNA
Wyznaczyć równanie płaszczyzny przechodzącej przez punkty
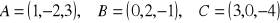
.Napisać równanie płaszczyzny
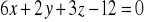
w postaci odcinkowej. Naszkicować tę płaszczyznę w układzie współrzędnych.Napisać równanie płaszczyzny przechodzącej przez oś OZ i punkt (1, 2, 3).
Wyznaczyć równanie płaszczyzny zawierającej prostą
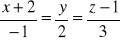
oraz punkt (3, -1, 0).Sprawdzić, czy punkty (1, 0, 0), (0, 2, 0), (0, 0, 3) i (2, -6, 6) są komplenarne. Jeżeli tak, to znaleźć ich płaszczyznę.
Napisać równanie parametryczne i kanoniczne prostej zawierającej punkty (-2, 0, 3), (3, -2. 5).
Napisać równanie prostej
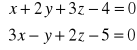
w postaci parametrycznej i kanonicznej.Wyznaczyć odległość:
punktu (0, -1, 3) od płaszczyzny
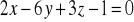
,punktu (-2, 0, 6) od prostej
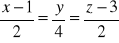
,prostej
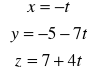
od płaszczyzny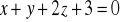
,między prostymi:
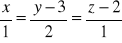
,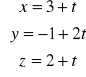
,między prostymi:
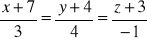
,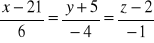
,między płaszczyznami:
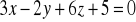
,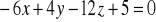
.Wyznaczyć rzut punktu (0, 3, 1) na płaszczyznę
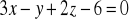
.Wyznaczyć rzut punktu (7, 1, 0) na prostą
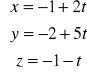
.Wyznaczyć rzut prostej
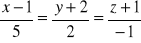
na płaszczyznę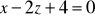
.
Wyszukiwarka
Podobne podstrony:
pytania kolokwium, Inżynieria Środowiska, I rok, geometria wykreślna
Geometria odpylacza cyklonowego, Studia - IŚ - materiały, Semestr 05, Technologie inżynierii środowi
przenikanie metoda sladow, Inżynieria Środowiska, I rok, geometria wykreślna
Powierzchnie matematyczne, pwr, W7 wydział inżynierii środowiska, Pwr IŚ Inżynieria Środowiska, Rysu
metoda pkt przebicia, Inżynieria Środowiska, I rok, geometria wykreślna
postac analityczna, SGGW Inżynieria Środowiska, SEMESTR 1, geologia, geologia (kurna mać), geologia,
LM inżynier środowiska
geometria analityczna
Geometria analityczna przyklady
Tarcie, Materiały, Inżynieria Środowiska, Semestr 2, Mechanika techniczna, egzaminy
Przedsiebi, inżynieria ochrony środowiska kalisz, z mix inżynieria środowiska moje z ioś pwsz kalis
Hydrologia - zaliczenie wyk, Inżynieria Środowiska, 3 semestr, Hydrologia
4 jedrzejów łaczyn, Inżynieria Środowiska PŚk, Semestr 2, Hydrogeologia 1, projekt
1, Inżynieria Środowiska, semestr 2 UR, Geodezja, wykłady, ściąga
instrukcja - HYDROLIZA SOLI, Inżynieria środowiska, inż, Semestr II, Chemia ogólna, laboratorium
sciaga3, Inżynieria środowiska, I semestr, Biologia i ekologia, materiały na egzamin z biol
Projekt 2 - Spis treści, Inżynieria Środowiska, Oczyszczanie Gazów
pHmetr-instrukcja obsługi, Inżynieria środowiska, inż, Semestr II, Chemia ogólna, laboratorium
Ekonomia środowiska 8, Inżynieria Środowiska, Ekonomia Środowiska
więcej podobnych podstron