Bogdan Płachta
MATERIAŁY DO LABORATORIUM Z ELEKTROTECHNIKI TEORETYCZNEJ
1. BADANIE SYMETRYCZNYCH UKŁADÓW TRÓJFAZOWYCH. (ćw. 7)
Układem wielofazowym nazywamy zbiór obwodów elektrycznych, w których działają odpowiednio połączone (skojarzone) sinusoidalnie zmienne wymuszenia o jednakowej częstotliwości, przesunięte względem siebie w fazie. Z uwagi na jednakową częstotliwość wymuszenia wytwarzane są w jednym źródle energii zwanym prądnicą lub generatorem, a także w układach zwiększających liczbę obwodów np. transformator wielofazowy. Przy tym fazą nazywa się jeden obwód prądnicy czy też transformatora.
Wartości chwilowe napięć fazowych układu wielofazowego można zapisać w postaci równań:
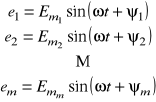
W praktyce stosuje się tzw. układy symetryczne ![]()
fazowe, które spełniają dwa warunki:
![]()
![]()
o liczbie faz ![]()
Układy ![]()
fazowe budowane są na bazie generatorów i stosuje się je do wytwarzania, przesyłu a także do przetwarzania energii elektrycznej. Układy 6, 12, 24 − fazowe budowane są na bazie transformatorów i używane są do prostowania za pomocą układów energoelektroniki w układach zasilania trakcji kolejowej i tramwajowej. Z uwagi na szerokie zastosowanie w praktyce w dalszych rozważaniach zajmować się będziemy tylko układami trójfazowymi. Obwodem trójfazowym symetrycznym nazywa się układ trzech jednakowych wymuszeń o tej samej amplitudzie i częstotliwości przesuniętych w fazie o ![]()
okresu.
Do przesyłu energii w układzie nieskojarzonym wykorzystuje się 6 przewodów, natomiast w układzie skojarzonym (rys.7.1) 3 lub 4 przewody − 3 przewody fazowe i jeden neutralny. Napięcie między przewodem fazowym a przewodem neutralnym nazywa się napięciem fazowym, a napięcia między przewodami fazowymi nazywa się napięciami przewodowymi. Napięcie międzyfazowe jest o ![]()
razy większe od napięcia fazowego i wyprzedza w fazie napięcie fazowe o kąt ![]()
. Suma geometryczna napięć międzyfazowych jest równa zero. Jeżeli jeszcze odbiornik jest symetryczny to w przewodzie neutralnym nie płynie prąd i przewód neutralny jest niepotrzebny. W praktyce stosuje się układy trójprzewodowe w sieciach elektroenergetycznych.
Oprócz skojarzenia odbiornika w gwiazdę (rys.7.1) możliwe jest połączenie w trójkąt (rys.7.2). Prądy płynące w każdym z przewodów fazowych w układzie trój kątowym, zwane są prądami przewodowymi, a prądy płynące między fazami odbiornika nazywa się prądami fazowymi. Dla układu symetrycznego ![]()
połączonego w trójkąt suma geometryczna napięć międzyfazowych jest równa zero. Napięcia międzyfazowe są dla odbiornika napięciami fazowymi. Prąd przewodowy jest ![]()
razy większy od prądu fazowego o kąt ![]()
. Jeżeli odbiornik połączony jest w gwiazdę to ![]()
oraz ![]()
, gdzie: ![]()
napięcie i prąd przewodowy, P − moc czynna układu.
Jeśli odbiornik połączymy w trójkąt to ![]()
oraz ![]()
, gdzie: ![]()
napięcie i prąd fazowy, P − moc czynna układu.
Udział w przetwarzaniu mocy obydwu układów
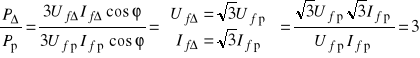
.
2. BADANIE NIESYMETRYCZNYCH UKŁADÓW TRÓJFAZOWYCH. (ćw. 8)
W praktyce oprócz układów symetrycznych (ćw.7) spotkać można odbiorniki jednofazowe o różnych wartościach impedancji i charakterach przyłączone do sieci trójfazowej. W związku z tym prądy będące odpowiedziami będą miały różną wartość amplitudy i różnicę faz początkowych przebiegów różną od ![]()
, np. sieci elektroenergetyczne NN. Obwody źródła najczęściej połączone są w podwójną gwiazdę tzw. zygzak, a odbiornik w gwiazdę z przewodem neutralnym (rys.8.1) .
Analizę układu wygonie przeprowadzić stosując metodę potencjałów węzłowych, gdyż liczba równań względem niewiadomych jest najmniejsza i wynosi ![]()
. Dla porównania liczba równań z metody prądów oczkowych wynosi ![]()
.
Algorytm analizy:
wybrać węzeł odniesienia w punkcie neutralnym źródła N,obliczyć potencjał węzła neutralnego odbiornika N' ze wzoru 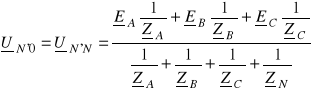
,
obliczyć napięcia fazowe na impedancjach odbiornika ![]()
dla ![]()
,
obliczyć prądy przewodowe 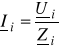
dla ![]()
obliczyć prąd w przewodzie neutralnym 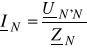
lub ![]()
.
Jeżeli ![]()
to odbiornik jest odbiornikiem symetrycznym i wówczas napięcie ![]()
oraz prąd w przewodzie neutralnym ![]()
, stąd można zastosować układ trójprzewodowy.
Jeżeli ![]()
to odbiornik jest odbiornikiem niesymetrycznym i wówczas napięcie ![]()
oraz prąd w przewodzie neutralnym ![]()
. Asymetria impedancji odbiornika powoduje asymetrię napięć na odbiorniku. Za pomocą wykresu wskazowego możliwe jest wtedy graficzne wyznaczenie napięcia ![]()
wymagające zastosowania między innymi cyrkla rys.8.2. Punkt przecięcia trzech okręgów o promieniach odpowiadających napięciu na odbiorniku wyznacza koniec wskazu napięcia ![]()
.
Jeżeli ![]()
i ![]()
to ![]()
i napięcia na odbiorniku są symetryczne oraz ![]()
, jest to najbardziej praktyczny przypadek dla sieci czteroprzewodowej.
Jeżeli ![]()
i ![]()
to ![]()
i napięcia na odbiorniku są niesymetryczne oraz ![]()
, jest to przypadek dla sieci trójprzewodowej bez przewodu neutralnego. Przy braku fazowej impedancji odbiornika tzw. zwarciu przewodu fazowego z punktem neutralnym odbiornika napięcie ![]()
jest równe napięciu zasilającemu tę fazę.
3. ELEKTRYCZNE OBWODY Z ELEMENTAMI NIELINIOWYMI O WYMUSZENIU STAŁYM. (ćw. 9)
Elektryczny obwód nieliniowy albo ogólniej elektryczny układ nieliniowy zbudowany jest z elektrycznych elementów nieliniowych lub częściowo z elementów liniowych i elementów nieliniowych. W granicznym przypadku układ nieliniowy powinien posiadać przynajmniej jeden element nieliniowy tzn. taki element, którego charakterystyka ![]()
nie przedstawia linii prostej (rys.9.1).
Celem ćwiczenia jest wyznaczenie charakterystyk napięciowo-prądowych elementów nieliniowych, także badanie obwodów elektrycznych z tymi elementami w różnych układach połączeń oraz stosowanie metod graficznych do rozwiązywania układów nieliniowych.
Wprowadza się dwa parametry charakteryzujące element nieliniowy w danym punkcie pracy:
a) parametr statyczny;
np. rezystancja statyczna dla elementu z rys.9.1
![]()
b) parametr dynamiczny;
np. rezystancja dynamiczna dla elementu z rys.9.1
![]()
gdzie: mu - skala dla osi napięcia (u);
mi - skala dla osi prądu (i).
Parametr statyczny jest zawsze wartością dodatnią, natomiast parametr dynamiczny może przyjmować wartości dodatnie, ujemne lub równe zero.
Jeżeli w obwodzie występuje element nieliniowy to w tym obwodzie nie jest spełniona zasada proporcjonalności i zasada superpozycji. Stosuje się wtedy metody przybliżone: analityczną, graficzną, graficzno-analityczną i numeryczną. Analizę prostych układów nieliniowych tzn. takich których liczba elementów nieliniowych jest niska łatwo przeprowadzić metodami graficznymi. Rozróżnia się przy tym metodę charakterystyki łącznej tzw. charakterystyki zastępczej (rys.9.3) a także metodę charakterystyki odwróconej tzw. metodę przecięcia charakterystyk (rys.9.3-4).
W obwodach złażonych należy postępowanie graficzne z rys. 9.3-4 stosować wielokrotnie.
4. BADANIE ZAWARTOŚCI HARMONICZNYCH W OKRESOWYM PRZEBIEGU PRĄDU DŁAWIKA. (ćw. 10)
Przebieg w czasie t wielkości obwodowej ![]()
zwanej przebiegiem wartości chwilowej, który dla dowolnej liczby naturalnej n i stałego przedziału czasu T zwanego okresem, spełnia warunek ![]()
nazywa się przebiegiem okresowym. Jeśli przebieg okresowy jest przebiegiem o kształcie innym niż przebieg sinusoidalny nazywa się przebiegiem odkształconym. Dowolny przebieg okresowy spełniający warunki Dirichleta można przedstawić w postaci nieskończonego szeregu Fouriera
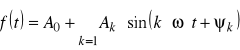
gdzie: 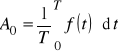
- średnia wartość funkcji![]()
w ciągu okresu tzw. składowa stała,
k - numer przebiegu sinusoidalnego o pulsacji k - razy większej od pulsacji podstawowej równej ![]()
tzw. rząd harmonicznej,
![]()
- amplitudy k-tych harmonicznych,
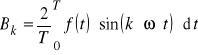
- składnik k-tej harmonicznej z sinusami,
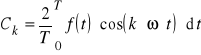
- składnik k-tej harmonicznej z kosinusami,
![]()
- faza początkowa k-tej harmonicznej, z poprawką β wynikającą ze stosowania kalkulatorów, tablic itp.
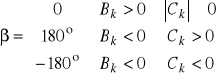
Korzystając z rozwinięcia funkcji w szereg Fouriera obliczenia ogranicza się do skończonej liczby wyrazów szeregu. Obliczenia można także ograniczyć w przypadku jeśli funkcja ![]()
wykazuje symetrię i tak jeżeli:
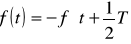
tzn.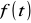
jest funkcją antysymetryczną, w szeregu Fouriera nie występują składowa stała i harmoniczne parzyste; tego typu przebiegi pojawiają się w odpowiedziach prądowych w obwodach zawierających elementy z ferromagnetykiem na napięciowe wymuszenie sinusoidalne np. około 90% przebiegów w elektroenergetyce,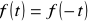
tzn.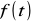
jest funkcją parzystą tzn. funkcją symetryczną względem osi rzędnej, w szeregu Fouriera nie występują wyrazy z sinusami,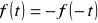
tzn.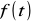
jest funkcją nieparzystą tzn. funkcją symetryczną względem początku układu współrzędnych, w szeregu Fouriera nie występują wyrazy z kosinusami.
Praktycznie interesujący jest przypadek, kiedy znany jest przebieg odkształcony np. z oscyloskopu a poszukiwane są współczynniki szeregu Fouriera. Do wyznaczenia współczynników trygonometrycznego szeregu Fouriera stosuje się metody pomiarowe i symulacyjne metody matematyczne.
Wśród metod matematycznych stosuje się numeryczne wyznaczenie powyższych całek wg metody Perri`ego i całego szeregu Fouriera zwaną interpolacją trygonometryczną. W tym celu należy wykonać równomierną dyskretyzację ciągłego przebiegu ![]()
w przedziale ![]()
. Dyskretyzacja polega na wyborze m i-tych punktów równoodległych od siebie w czasie o ![]()
i przyporządkowaniu wartości funkcji ![]()
w tych punktach, przy czym liczba m wynika z najwyższego numeru h spektrum harmonicznych ![]()
, oraz dla i-tej chwili czasowej ![]()
, wartość ![]()
odczytuje się np. z oscyloskopu dla ![]()
(rys. 10.1).
.
W numerycznej metodzie Perri'ego określania współczynników szeregu Fouriera, z uwagi na skończoną liczbę h obliczanych harmonicznych oraz postać dyskretną wartości funkcji ![]()
powyższe całki analityczne zastępuje się przybliżonymi wzorami algebraicznymi, a analityczny wzór szeregu Fouriera przybiera postać rekurencyjnego wzoru interpolacji trygonometrycznej o postaci
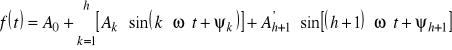
gdzie: 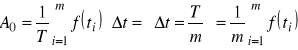
![]()
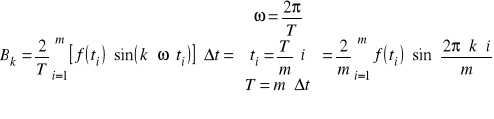
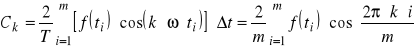
![]()
![]()
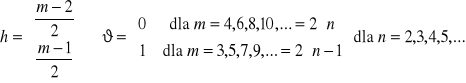
Oprócz metod matematycznych stosuje się także metody pomiarowe za pomocą urządzenia zwanego analizatorem harmonicznych, także pomiaru modułu harmonicznych napięcia na znanej rezystancji za pomocą selektywnego woltomierza. Prostą metodą pomiaru modułu k-tej harmonicznej jest metoda watomierza, przy czym obwód napięciowy zasilany jest z osobnego źródła napięcia, np. z elektronicznego generatora mocy, o regulowanej częstotliwości w zakresie wielokrotności harmonicznej podstawowej.
Wskazanie watomierza jest proporcjonalne do mocy czynnej k-tej harmonicznej 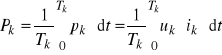
. Niech obwód napięciowy watomierza zasilany będzie nastawionym napięciem o równaniu ![]()
, a przez obwód prądowy watomierza płynie badany prąd odkształcony zawierający wyższe harmoniczne o równaniu dla k-tej harmonicznej ![]()
, przy czym ![]()
, to ![]()
. Niech błąd nastawy częstotliwości napięcia obwodu napięciowego watomierza z częstotliwością k-tej harmonicznej prądu będzie równy ![]()
i wiążącej się z tym błędem uchyb pulsacji![]()
to wskazanie watomierza
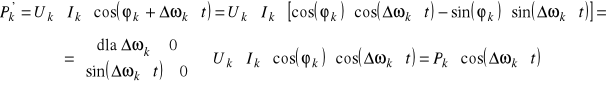
jest proporcjonalne do mocy czynnej k-tej harmonicznej i bardzo wolno zmieniającej się w czasie funkcji ![]()
dającej ruch harmoniczny wskazówki watomierza. Chcąc wyznaczyć wartość skuteczną prądu k-tej harmonicznej należy brać pod uwagę maksymalne wskazania watomierza k-tej harmonicznej mocy pozornej, gdyż ![]()
tzn. ![]()
. Następnie można obliczyć wartość skuteczną k-tej harmonicznej w przebiegu prądu ze wzoru ![]()
.
Celem ćwiczenia jest analiza zawartości harmonicznych w odkształconym prądzie dławika z rdzeniem ferromagnetycznym metodą z watomierzem selektywnego pomiaru mocy oraz symulacyjną metodą Perry′ego. Celem ćwiczenia jest także obserwacja na ekranie oscyloskopu pętli histerezy pakietu rdzenia dławika wykonanego z blach transformatorowych.(Patrz wprowadzenie do ćw. 15).
Obserwacja pętli histerezy materiałów ferromagnetycznych rdzeni dławików, rdzeni transformatorów i rdzeni przetworników elektromaszynowych wymaga zastosowania w układzie pomiarowym oscyloskopu układu całkującego RC (rys. 10.2).
Rys. 10.2. Schemat pomiarowy do obserwacji histerezy.
Niech uzwojenie pierwotne transformatora pobudzane jest z sinusoidalnego źródła napięcia o stałej w czasie wartości skutecznej powodującej nasycanie się rdzenia ferromagnetycznego. Na zaciski wejściowe oscyloskopu dwukanałowego XY podawane są napięcia, u z rezystora R1 oraz uC z kondensatora C. Okazuje się że dołączone na wejście X oscyloskopu napięcie u jest proporcjonalne do natężenia pola magnetycznego wewnątrz magnetowodu rdzenia transformatora zgodnie z zależnością
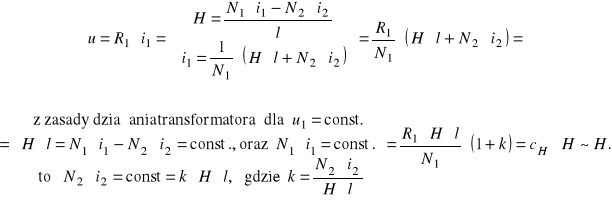
.
gdzie: ![]()
- liczba zwojów uzwojenia pierwotnego i uzwojenia wtórnego transformatora,
l - zastępcza długość linii sił pola magnetycznego równa zastępczej długości rdzenia,
![]()
- stała zależna od konstrukcji transformatora i elementów obwodu pierwotnego i wtórnego dla ![]()
.
Natomiast dołączone na wejście Y oscyloskopu napięcie uC proporcjonalne jest do indukcji magnetycznej B wewnątrz magnetowodu rdzenia transformatora wg zależności
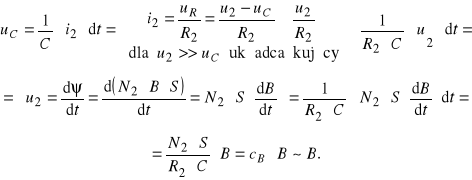
gdzie: ψ - strumień magnetyczny skojarzony z uzwojeniem wtórnym transformatora,
S - pole przekroju poprzecznego rdzenia ferromagnetycznego transformatora,
![]()
- stała zależna od konstrukcji transformatora i elementów całkującego obwodu wtórnego.
Na ekranie oscyloskopu pojawia się obraz zależności ![]()
w postaci krzywej zamkniętej proporcjonalny do kształtu krzywej histerezy ferromagnetyka rdzenia ![]()
(rys. 10.3).
Dysponując obrazem z oscyloskopu krzywej ![]()
można dokonać następującego przeliczenia na postać krzywej magnesowania ![]()
- odczyt dla osi rzędnej
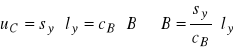
- odczyt dla osi odciętej
![]()
gdzie: ![]()
- stałe wzmocnienia kanałów X i Y oscyloskopu w![]()
,
![]()
- szerokość i wysokość obrazu w ![]()
dla osi H i dla osi B,
![]()
- stałe osi H i osi B wynikające ze zamiany współrzędnych napięcia na współrzędne natężenie pola H i indukcji B obliczane według zależności wyżej.
9
U
B
V
W
A
C
L1
L2
L3
eA
eB
eC
ZA
ZB
ZC
N
N'
eA=Em sin ωt
eB=Em sin (ωt−120°)
eC=Em sin (ωt+120°)
Rys. 7.1. Układ trójfazowy symetryczny
ZA=ZB=ZC=Z
ZAB
ZBC
A
B
C
U
Uf
If
I
Rys.7.2. Trójfazowy układ skojarzony w trójkąt.
ZCA
U
B
V
W
A
C
L1
L2
L3
EA
EB
EC
ZA
ZB
ZC
N
N'
Rys. 8.1. Układ trójfazowy czteroprzewodowy.
ZN
IA
IB
IC
IN
EA
EB
EC
UA
UC
UB
UN'N
IA
IB
IC
IN'N
Rys.8.2.Wykres topograficzny trójfazowego układu czteroprzewodowego dla . Punkt przecięcia okręów o promieniach odpowiadających napięciu na impedancjach odbiornika wyznacza koniec wskazu UN'N. względem początku układu współrzędnych.
u
i
U0
I0
Ppr.(A , B)
0
Em
Jm
Rys.9.1. Przykładowa charakterystyka elementu nieliniowego.
u
R
0
Rys. 9.2. Charakterystyka parametru np. rezystancji R elementu nieliniowego z rys. 9.1.
I1=f1(U1)
I
I=f (U1+U2)
I2=f2(U2)
U
0
U1
U2
E
I
I1=f1(U1)
I
I=f (U1+U2)
I2=f2(U2)
U
0
U1
U2
E
I
a)
I2=f2 (E-U1)
I1=f1(U1)
I
U
0
U1
E-U1
E
I
b)
I2=f2 (-U2)
Rys. 9.3. Metody graficzne dla połączenia szeregowego dwóch elementów nieliniowych:
a) charakterystyki łącznej,
b) charakterystyki odwróconej.
I1=f1(U1)
I
I1+I2=f (U)
I2=f2(U2)
U
0
U
I2
I1
J
I1=f1(U1)
I
J-I2=J-f (U)
I2=f2(U2)
U
0
U
J-11
I1
J
-I2=-f (U)
Rys. 9.4. Metody graficzne dla połączenia równoległego dwóch elementów nieliniowych:
a) charakterystyki łącznej,
b) charakterystyki odwróconej.
T
t
1
2
k
m
i
0
Rys.10.1.
Przykład dyskretyzacji jednego okresu zmian ciągłego przebiegu np. prądu dławika przy napięciowym wymuszeniu sinusoidalnym.
Y
X
uC
C
uR
u2
R
R1
u
u1
i1
i2
Rys. 10.3. Obraz na ekranie oscyloskopu histerezy magnetycznej rdzenia wykonanego z blach ferromagnetycznych.
Wyszukiwarka
Podobne podstrony:
Badanie tranzystorów unipolarnych typu, ˙wiczenie nr 10
Cwiczenia nr 10 (z 14) id 98678 Nieznany
Zestaw ćw nr 10, zestawy ćwicze gimnastycznych, zestawy ćwiczeń gimnastycznych
Zeszyt Ćwiczeń nr 10
Spr.nr 10, Studia, Chemia, chemia7
Koszykówka nr 10
NR 10 TAK! 50 SEKRETÓW
Wybierz Życie Nr!10 wrzesień 10 r
112, (112)B, ˙wiczenie nr 112
wszystko, 06 Załącz nr 10 program kursu
(ZDERZ~1, ˙wiczenie nr ???
Laborka nr 10, 2
więcej podobnych podstron