Szeregi Taylora i Maclaurina
Definicja (Szeregu Taylora)
Niech funkcja f ma w punkcie x0 pochodne dowolnego rzędu. Szereg potęgowy
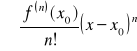
nazywamy szeregiem Taylora funkcji f o środku w punkcie x0. Jeżeli x0=0, to szereg ten nazywamy szeregiem Maclaurina funkcji f.
Uwaga
Ze zbieżności szeregu Maclaurina funkcji f wynika, że jego suma jest równa tej funkcji.
Twierdzenie (O rozwijaniu funkcji w szereg Taylora).
Jeżeli:
funkcja f ma w otoczeniu U(x0) pochodne dowolnego rzędu,
dla każdego x∈U(x0)
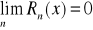
, gdzie
![]()
oznacza n-tą resztę we wzorze Taylora dla funkcji f.
Wówczas:
![]()
dla każdego x∈U(x0).
Uwaga
Zamiast założenia (20 można przyjąć:
(2') wszystkie pochodne funkcji f są wspólnie ograniczone, tzn.
![]()
Twierdzenie (O jednoznaczności rozwinięcia funkcji w szereg potęgowy)
Jeżeli ![]()
dla każdego x z pewnego otoczenia U(x0), to ![]()
dla n=0,1,2,…
Ciągi i szeregi ortogonalne
Niech V={f:[a,b]→R; f-całkowalna w sensie Riemanna na [a,b]}. V jest przestrzenią liniową nad ciałem liczb rzeczywistych z dodawaniem funkcji i mnożeniem funkcji przez liczbę. W przestrzeni V określamy iloczyn skalarny następująco:
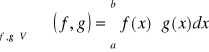
;
oraz określamy normę kwadratową funkcji f:
![]()
.
Definicja
Ciąg funkcyjny {fn}n∈N nazywamy ortogonalnym na [a,b], jeżeli (fn,fm)=0 dla n≠m i ![]()
dla wszystkich n.
Definicja
Jeżeli {cn}n∈N jest ciągiem liczbowym, zaś {fn}n∈N jest ciągiem funkcyjnym ortogonalnym w przedziale [a,b], to szereg funkcyjny ![]()
nazywamy szeregiem ortogonalnym.
Twierdzenie (O szeregu ortogonalnym)
Jeżeli szereg ortogonalny ![]()
jest jednostajnie zbieżny do funkcji f w przedziale [a,b] i funkcja ta jest całkowalna na [a,b], to współczynniki cn wyrażają się wzorami:
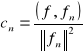
Uwaga
Dla każdego ciągu ortogonalnego w przedziale [a,b] i funkcji f całkowalnej w tym przedziale istnieje więc co najwyżej jeden taki szeteg ortogonalny, który jest jednocześnie zbieżny w tym przedziale do funkcji f. Jeżeli taki szereg istnieje, to jest nim szereg ![]()
, gdzie 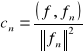
.
Liczby cn określone powyższymi wzorami nazywamy współczynnikami Fouriera funkcji f względem ciągu {fn}n∈N.
Wyszukiwarka
Podobne podstrony:
sciaga egzamin 1, IT PJWSTK GD, Semestr II, AM I
ściąga 2 egzamin, Notatki UTP - Zarządzanie, Semestr II, Technologie informacyjne
ściąga 1 egzamin, Notatki UTP - Zarządzanie, Semestr II, Technologie informacyjne
ściąga 3 egzamin, Notatki UTP - Zarządzanie, Semestr II, Technologie informacyjne
egzamin - sciaga 22- teoria, STUDIA budownictwo, SEMESTR II, materiały budowlane
egzamin - sciaga 22- teoria, STUDIA budownictwo, SEMESTR II, materiały budowlane
sciaga pugp, Gospodarka Przestrzenna, GP semestr II
sciaga na lab.ps, STUDIA, SEMESTR II, Materiały Metalowe, mm
Biogeografia - ściaga egzamin, ochrona środowiska UJ, I semestr SUM, biogeografia
PYTANIA EGZAMINACYJNE 2, Prywatne, psychologia wsfiz, semestr II, Negocjacje wykłady
egzamin - testy1, STUDIA budownictwo, SEMESTR II, materiały budowlane
egzamin - promocja zdrowia, administracja semestr II, promocja zdrowia
sciaga odlewanie, Politechnika Poznańska (ETI), Semestr I i II, Metalurgia I Odlewnictwo
sciaga www.przeklej.pl, MiBM, semestr II, Odlewnictwo, INNe
EGZAMIN BIOCHEMIA, Zootechnika SGGW, semestr II, biochemia
Ekologia - egzamin(, Studia UR OŚ, semestr II, ekologia
ściąga stata, Notatki UTP - Zarządzanie, Semestr II, Statystyka
więcej podobnych podstron