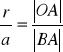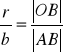Międzyszkolne Zawody Matematyczne

Klasa I - profil ogólny

Etap wojewódzki - 26.04.2003 rok

Czas rozwiązywania zadań - 150 minut

Zadanie 1 (6 pkt)

W liczbie sześciocyfrowej, podzielnej przez 10985 cyfra jedności jest równa cyfrze tysięcy, cyfra dziesiątek jest równa cyfrze dziesiątek tysięcy i cyfra setek jest równa cyfrze setek tysięcy.

Znajdź tę liczbę.

Zadanie 2 (6 pkt)

1. Narysuj wykres funkcji:

y =

2. Określ w zależności od parametru m liczbę rozwiązań równania:

= 2x + m

Zadanie 3 (6 pkt)

Właściciel księgarni kupuje podręczniki w hurtowni i sprzedaje je po 21 zł za sztukę.

Cena podręcznika w księgarni (detaliczna) jest o 40% wyższa niż cena w hurtowni.

1. Ile kosztuje jeden podręcznik w hurtowni?

2. Oblicz, jakim procentem ceny sprzedaży jest zysk księgarza.

3. Ile podręczników musi sprzedać księgarz, aby jego zysk przekroczył 1000 zł?

4. Ze względu na dużą konkurencję, właściciel księgarni postanowił obniżyć cenę tak,

aby zysk nie przekroczył 25% ceny sprzedaży.

Jaką maksymalną cenę na podręcznik może ustalić, aby być w zgodzie ze swoim

postanowieniem?

Zadanie 4 (6 pkt)

W prostokącie ABCD bok AB jest dwa razy dłuższy od boku BC. Zbudowano trójkąt

równoboczny ABE, zakrywający częściowo prostokąt ABCD. Jaką część prostokąta zakrywa

trójkąt ABE?

Zadanie 5 (6 pkt)

Przyprostokątne trójkąta prostokątnego mają długości a i b. Okrąg o promieniu długości r

jest styczny do obu przyprostokątnych, a jego środek leży na przeciwprostokątnej.

Wykaż, że:

Życzymy powodzenia

Kryteria oceniania dla klasy I - profil ogólny

Nr zad	Wykonana czynność	Pkt
1	Zapisanie liczby sześciocyfrowej w postaci: 100000a + 10000b + 1000c + 100a + 10b +c, gdzie a, b, c są cyframi i a 0	1
		Przekształcenie sumy do postaci iloczynowej ; 1001(100a + 10b +c)	1
		Zapisanie warunku, że liczba jest podzielna przez 10985: 1001(100a + 10b +c) = 10985n	1
		Podzielenie ostatniej równości przez NWD(1001; 10985)=13, czyli przekształcenie do postaci: 77(100a + 10b +c) = 845n	1
		Zapisanie, że n = 77 i 100a + 10 b + c = 845	1
		Podanie odpowiedzi: 845845	1
	2	Przekształcenie wzoru funkcji do postaci: y =	1
		- 2x dla x < - 2 Zapisanie wzoru funkcji w postaci: y = 4 dla - 2 2x dla x	1,5
		Narysowanie wykresu funkcji	1
		Narysowanie wykresu funkcji y = 2x	1
		Określenie liczby rozwiązań równania w zależności od m; dla m = 0 - nieskończenie wiele rozwiązań, dla m< 0 - brak rozwiązań, dla m>0 - jedno rozwiązanie	1,5
	3	Wyznaczenie ceny podręcznika w hurtowni: 15 zł	1
		Obliczenie, jakim procentem ceny sprzedaży jest zysk: 28 %	1
		Ustalenie liczby sprzedanych podręczników: co najmniej 167	1
		Zapisanie warunku do podpunktu d) w postaci równania /nierówności: 100% = 25%	1p
		Rozwiązanie równania/nierówności	1
		Sformułowanie odpowiedzi: maksymalna cena może wynosić 20 zł	1
	4	Wykonanie rysunku wraz z oznaczeniami	1
		Obliczenie pola prostokąta : 2a^2, gdzie =a	1
		Obliczenie długości krótszej przyprostokątnej trójkąta zawartego w prostokącie : x =	1
		Obliczenie pola trapezu zawartego w prostokącie ;	2
		Obliczenie stosunku pola trapezu do pola prostokąta: 1 -	1
	5	Wykonanie rysunku z oznaczeniami	1
		Wskazanie par trójkątów podobnych z powołaniem się na odpowiednie cechy	1
		Zapisanie równości: , gdzie AB jest przeciwprostokątną a O - środkiem okręgu	1
		Zapisanie równości:	1
		Dodanie dwóch poprzednich równości stronami i zapisanie w postaci:	1
		Przekształcenie ostatniego wzoru do postaci:	1

Za poprawnie rozwiązane zadania metodą inną aniżeli opisana w schemacie punktowania należy przyznać maksymalną liczbę punktów.

Jeżeli uczeń rozwiązał zadanie inną metodą i popełnił błędy to należy określić i ocenić czynności równoważne do wymienionych w schemacie.

---