Ćwiczenia 5. MICROFIT - opis narzędzia.

Zadanie. Niech Y_t = α₀ + α₁X_1t + α₂X_2t + α₃X_3t + α₄X_4t + ξ_t, gdzie:

Y_t - zmiany produkcji w przedsiębiorstwie [mld zł],

X_1t - zatrudnienie [tys. osób],

X_2t - wartość maszyn i urządzeń [mld zł],

X_3t - czas przestoju maszyn [l. dni],

X_4t - nakłady inwestycyjne [mln zł],

t € [1991 - 2000].

Lata	Yt	X1t	X2t	X3t	X4t
1991	10	6	8	14	12
1992	10	6	8	14	12
1993	16	10	12	18	12
1994	16	10	12	18	14
1995	12	8	8	18	10
1996	14	10	8	18	12
1997	20	12	14	24	14
1998	20	12	16	24	12
1999	20	12	16	26	12
2000	22	14	18	26	10

Parametry modelu oszacowano klasyczną metodą najmniejszych kwadratów. Procedura szacowania parametrów strukturalnych oraz parametrów struktury stochastycznej opracował prof. Bashem Pesaran wraz z dr Bahram Pesaran i wydana przez Oxford University Press pod nazwą MICROFIT.

Ordinary Least Squares Estimation

***************************************************************************

I.

Dependent variable is Y

10 observations used for estimation from 1991 to 2000

II.

Regressor Coefficient Standard Error T-Ratio[Prob]

C -3.97930 1.022100 -3.8933[0.011]

X1 0.86241 0.105200 8.1979[0.000]

X2 0.37075 0.061860 5.9935[0.002]

X3 0.16983 0.066925 2.5377[0.052]

X4 0.29246 0.070716 4.1357[0.009]

***************************************************************************

III.

1. R-Squared 0.99785 6. R-Bar-Squared 0.99614

2. S.E. of Regression 0.27483 7. F-stat. F(4,5) 581.2805[0.000]

3. Mean of Dependent Variable 16.0000 8. S.D. of Dependent Variable 4.4222

4. Residual Sum of Squares 0.37766

5. DW-statistic 2.87240

***************************************************************************

IV. Diagnostic Tests

***************************************************************************

* Test Statistics * LM Version * F Version *

***************************************************************************

* A:Serial Correlation *CHSQ(1)= 3.1360[0.077]**************F(1,4)= 1.8275[0.248] *

* B:Functional Form *CHSQ(1)= 0.64114[0.423]*************F(1,4)= 0.27402[0.628]*

* C:Normality *CHSQ(2)= 0.80713[0.668]*************Not applicable *

* D:Heteroscedasticity*CHSQ(1)= 0.48283[0.487]*************F(1,8)= 0.40586[0.542]*

***************************************************************************

A: Lagrange multiplier test of residual serial correlation

B:Ramsey's RESET test using the square of the fitted values

C:Based on a test of skewness and kurtosis of residuals

D:Based on the regression of squared residuals on squared fitted values

V. Residuals and Fitted Values of Regression

***************************************************************************

Based on OLS regression of Y on: C X1 X2 X3 X4

10 observations used for estimation from 1991 to 2000

***************************************************************************

Observation Actual Fitted Residual

1991 10.0000 10.0484 -0.048359

1992 10.0000 10.0484 -0.048359

1993 16.0000 15.6603 0.339670

1994 16.0000 16.2453 -0.245250

1995 12.0000 11.8676 0.132410

1996 14.0000 14.1773 -0.177320

1997 20.0000 19.7306 0.269430

1998 20.0000 19.8872 0.112840

1999 20.0000 20.2268 -0.226830

2000 22.0000 22.1082 -0.108230

***************************************************************************

Jakie informacje o oszacowanych elementach struktury modelu zawiera wydruk rezultatów estymacji?

Część I. Zawarto w niej o zmiennej objaśnianej, liczebności próby statystycznej oraz okresie, którego dotyczy próba statystyczna.

Część II. Cztery kolumny zawierają kolejno:

1. informacje o zmiennych objaśniających,

2. oszacowane parametry strukturalne,

3. wartości błędów średnich szacunku parametrów,

4. wartości statystyki T, która jest ilorazem oceny parametru do błędu średniego szacunku, ponadto wartość statystyki Prob /jej rola i znaczenie zostanie przedstawiona w procesie weryfikacji, Prob określa prawdopodobieństwo przyjęcia przez statystykę wartości nie mniejszej od wartości próbkowej przy założeniu prawdziwości
   /.

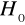
Część III. Wartości:

1. 
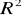
   współczynnika determinacji,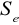

2. 
   standardowy błąd reszt,

3. wartość przeciętna zmiennej objaśnianej,

4. suma kwadratów reszt /reszty - różnice pomiędzy wartościami empirycznymi i teoretycznymi/,

5. 
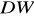
   statystyka Durbina Watsona,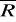

6. 
   ² skorygowany współczynnik determinacji,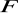

7. 
   statystyka, ma rozkład Fishera - Snedecora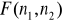
   , gdzie: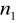
   - liczba stopni swobody licznika statystyki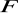
   ,
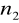
   - liczba stopni swobody mianownika statystyki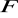
   ;
   ,

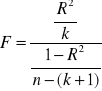
8. odchylenie standardowe zmiennej objaśnianej,

Część IV. Testy diagnostyczne. Budowę modelu można było zakończyć w wyniku przyjęcia szeregu założeń dotyczących:

1. zbioru zmiennych objaśniających opisujących zmiany zmiennej objaśnianej,

2. postaci analitycznej relacji pomiędzy zbiorem zmiennych objaśniających zmienną objaśnianą,

3. losowości składnika losowego,

4. stałości wariancji składnika losowego,

5. zgodności rozkładu składnika losowego z rozkładem normalnym,

6. wartości przeciętnej składnika losowego,

7. symetria składnika losowego,

8. braku autokorelacji składnika losowego.

Pakiet MICROFIT korzysta z czterech testów diagnostycznych:

1. testu Godfreya do badania istotności autokorelacji rzędu 1-go do 4-go,

2. testu Ramseya do weryfikacji przyjętej postaci analitycznej modelu,

3. testu Jarque'a-Bera do weryfikacji zgodności rozkładu składnika losowego z rozkładem normalnym,

4. testu do weryfikacji rozkładu składnika losowego w czasie, z założenia przyjmujemy, iż wariancja składnika losowego jest stała w czasie.

Statystyki wszystkich czterech testów diagnostycznych zdefiniowano dla dwóch sprawdzianów. Sprawdzian
dla dużych prób oraz
, dla prób małych.

Część V. Zawiera dane o wartościach empirycznych o zmiennej objaśnianej
, są to dane bazowe o zmiennych modelu /kolumna 2/. W kolumnie 3 tej części, umieszczono wartości teoretyczne zmiennej
, natomiast kolumna 4 zawiera reszty modelu, są realizacjami składnika losowego i są różnicami pomiędzy wartościami empirycznymi oraz teoretycznymi.

Wartości teoretyczne:

Lata	Wartości teoretyczne
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000

---