Ekonomia matematyczna I

Prowadzący ćwiczenia

mgr inż. Piotr Betlej

Analiza marginalna

Podstawowe pojęcia i umiejętności

Przychód całkowity - TR - przychód uzyskany ze sprzedaży wszystkich produktów po określonej cenie.

Koszt całkowity - TC - jest sumą kosztów stałych i kosztów zmiennych.

Zysk całkowity - ∏ - jest to różnica między przychodem całkowitym osiąganym przez przedsiębiorstwo a kosztem całkowitym produkcji dla danej wielkości produkcji ∏ = TR - TC.

Przychód przeciętny (średni) - AR - jest przychodem całkowitym przypadającym na jednostkę produktu,

Koszt przeciętny (średni) - AC - jest kosztem całkowitym przypadającym na jednostkę produktu,

Zysk przeciętny (średni) - A∏ - jest zyskiem całkowitym przypadającym na jednostkę produktu,

Przychód marginalny (krańcowy) - MR (marginal revenue) - jest to dodatkowy przychód wynikający ze zwiększenia o jednostkę produkcji i sprzedaży.

Koszt marginalny (krańcowy) - MC (marginal cost)- jest to zmiana kosztu całkowitego ∆TC wynikającą za zmiany wielkości produkcji o dodatkową jednostkę ∆Q,

Zysk marginalny (krańcowy) - M∏ - jest to zmiana zysku całkowitego ∆∏ wynikającą za zmiany wielkości produkcji o dodatkową jednostkę ∆Q,

Koszty stałe - koszty niezależne od rozmiarów produkcji, występują tylko w krótkim okresie czasu, np. płace pracowników administracji i obsługi, koszty zużywania się budynków, maszyn, urządzeń, koszty użytkowania ziemi, wynajmu lokali, koszty kredytów, niektóre podatki.

Koszty zmienne - koszty zmieniające się wraz ze zmianami wielkości produkcji, występują zarówno w krótkim jak i w długim okresie czasu, do kosztów tych zaliczamy płace pracowników produkcyjnych, koszty surowców, materiałów, półproduktów, koszty energii, wody.

Zastosowanie pochodnej funkcji

Zależność pomiędzy kosztem całkowitym a kosztem przeciętnym

Dla danej funkcji koszty całkowitego TC funkcja kosztu przeciętnego AC będzie wyrażać się następującym wzorem:

, skąd

Przykład:

Dla danej funkcji kosztu całkowitego: TC = Q­­³-4Q²-10Q+75 funkcja kosztu przeciętnego AC jest równa
AC = TC/Q = (Q­­³-4Q²-10Q+75)/Q= Q­­²-4Q-10+75/Q

Zależność pomiędzy kosztem całkowitym a kosztem krańcowym (marginalnym)

Dla dane funkcji kosztu całkowitego TC funkcja kosztu krańcowego MC (dla nieskończenie małego przychodu produkcji) jest granicą ilorazu ∆C/∆, czyli pochodną funkcji TC:

Wynika to z następującej zależności:

Należy zwrócić uwagę na fakt, iż koszt stały występujący w równaniu kosztu całkowitego znika podczas obliczania dC/dQ, więc wielkość kosztu stałego nie wpływa na koszt krańcowy.

Przykład:

Dla danej funkcji kosztu całkowitego: TC = Q­­³-4Q²-10Q+75 funkcja kosztu krańcowego MC jest pochodną funkcji TC czyli dC/dQ = 3Q^2­­-8Q+10.

Wyznaczanie zysku maksymalnego przy podanej funkcji zysku całkowitego

Przedsiębiorstwo osiąga maksymalny zysk przy takiej wielkości produkcji, przy której utarg ze sprzedaży dodatkowej jednostki produktu staje się równy kosztowi jej wytworzenia, gdy MR = MC, czyli zysk krańcowy jest równy zeru M∏ = 0.

Dla danej funkcji zysku całkowitego ∏ obliczamy funkcję zysku marginalnego M∏ jako pochodną funkcji zysku całkowitego:

Przyrównując to wyrażenie do zera, znajdujemy miejsca zerowe obliczonej funkcji. Będą to wartości w których zysk marginalny jest równy 0. Znając te wartości możemy wskazać, dla której wartości funkcja zysku całkowitego przyjmuje wartość maksymalną a dla której wartość minimalną.

W punkcie maksimum funkcja zysku zmienia swój kierunek z dodatniego na ujemny względem wzrostu produkcji, przy czym nachylenie funkcji wokół punktu zwrotnego maleje ze wzrostem produkcji. W punkcie minimum funkcja zmienia kierunek z ujemnego na dodatni, a jej nachylenie rośnie.

Z uwagi na tę różnicę potrzebna jest nam druga pochodna, która pozwoli odróżnić oba ekstrema. Obliczamy ją jako pochodną zysku krańcowego, tzn. pochodną od d∏/dQ. Jeśli druga pochodna jest ujemna (tzn. jeżeli nachylenie funkcji zysku maleje), to mamy do czynienia z lokalnym maksimum funkcji. Jeśli natomiast druga pochodna jest dodatnia, oznacza to, że dany punkt zwrotny stanowi lokalne minimum.

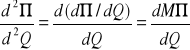
Przykład:

Dla danej funkcji zysku całkowitego: T∏ = 1,8Q² - 0,1Q­^­3 - 6Q -10 oblicz dla jakiej wielkości produkcji Q zysk całkowity przyjmuje wartość maksymalną. Oblicz zysk maksymalny dla wyznaczonej wartości.

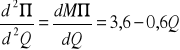
dla Q=2 d²∏/dQ² = 3,6-0,6*2 = 2,4

dla Q=10 d²∏/dQ² = 3,6-0,6*10 = -2,4

Zatem dla wartości Q=2 funkcja zysku posiada lokalne minimum a zysk całkowity wynosi -15,5; natomiast dla Q=10 funkcja zysku posiada lokalne maksimum a zysk całkowity wynosi 10.

Zadania do samodzielnego rozwiązania

Zadanie 1

Pewien menedżer twierdzi, że produkcję należy zwiększać dopóty, dopóki utarg przeciętny przewyższa koszt przeciętny. Czy takie postępowanie ma sens? Uzasadnij.

Zadanie 2

Załóżmy, że kierownictwo przedsiębiorstwa sporządziło następującą tablicę zysku krańcowego:

Przyrost produkcji	Przyrost zysków
0-1	-2,0
1-2	-1,5
2-3	-1,0
3-4	-0,5
4-5	+0,5
5-6	+2,0
6-7	+4,0
7-8	+3,2
8-9	+1,6
9-10	+0,4
10-11	-0,2
11-12	-0,7
12-13	-1,5

a) Jaka wielkość produkcji jest dla przedsiębiorstwa najbardziej opłacalna?

b) Przypuśćmy, że rzeczywisty zysk przedsiębiorstwa przy produkcji q = 0 wynosi -3 (z uwagi na koszty stałe). Jaka jest maksymalna wielkość zysku osiągalna w tym przedsiębiorstwie?

Zadanie 3

Mając dane funkcje przychodu całkowitego, wyznacz funkcje przychodu krańcowego
i przeciętnego, oblicz ich wartość dla danej wielkości sprzedaży i podaj interpretację:

a) TR = 4000q - 33q² q = 10

b) TR = 1400q - 6q² q = 100

c) TR = 5900q - 10q² q = 35

d) TR = 5q q = 20

Zadanie 4

Mając dane funkcje kosztu całkowitego, wyznacz funkcje kosztu krańcowego
i przeciętnego, oblicz ich wartość oraz dla danej wielkości produkcji i podaj interpretację:

a) TC = q³ - 8q² + 57q + 2 q = 5

b) TC = 0,3q³ - 8,5q² + 50q + 50 q = 18

c) TC = q³ - 5q² + 60q + 10 q = 35

d) TC = 1500 + 80q q = 20

Zadanie 5

Mając dane funkcje kosztu/przychodu przeciętnego, wyznacz funkcje kosztu/przychodu krańcowego
i całkowitego, oblicz ich wartość dla danej wielkości produkcji i podaj interpretację:

a) AC = q² - 8q + 57 + 2/q q = 5

b) AC = 3q + 7 + 12/q q = 4

c) AR = 4000 - 33q q = 35

d) AR = 1400 - 6q q = 20

Zadanie 6

Mając dane funkcje:

TR = 4350q - 136q² TC = q³ - 8q² + 150q + 675

wyznacz funkcje AR, MR, AC, MC, Π, AΠ.

Zadanie 7

Mając dane funkcje:

Π = -7,5q² + 1320q - 1500 TC = 1500 + 80q

wyznacz funkcje AΠ, AC, MC, TR, AR, MR.

Zadanie 8

Mając dane funkcje:

TR = 22q - 0,5q² AC = 0,3q³ - 8,5q + 50 + 90/q

wyznacz funkcje AR, MR, TC, MC, Π.

Zadanie 9

Mając dane funkcje:

TR = 4000q - 33q² Π = -2q³ - 30q² + 3600q - 5000

Wyznacz funkcje AR, MR, TC, AC, MC.

Zadanie 10

O ile w przybliżeniu zmieni się:

a) przychód całkowity oszacowany funkcją TR = 4000q - 33q² , jeżeli sprzedaż wzrośnie o jednostkę z poziomu równego 80. Ile w przybliżeniu procent wartości początkowej przychodu całkowitego będzie stanowiła ta zmiana?

b) przychód całkowity oszacowany funkcją TR = 22q - 0,5q² , jeżeli sprzedaż wzrośnie o jednostkę
z poziomu równego 10. Ile w przybliżeniu procent wartości początkowej przychodu całkowitego będzie stanowiła ta zmiana?

c) koszt całkowity oszacowany funkcją TC = 2q³ - 4q² + 140q + 845 , jeżeli produkcja wzrośnie
o jednostkę z poziomu równego 40. Ile w przybliżeniu procent wartości początkowej kosztu całkowitego będzie stanowiła ta zmiana?

Zadanie 11

Funkcja przychodu całkowitego dana jest wzorem: TR = 100q -10q² .

Uzupełnij poniższą tabelę, podaj interpretację zależności występującej pomiędzy wartościami funkcji przychodu całkowitego i krańcowego:

Q	TR(q)	MR(q)	AR(q)	MR(q) * 100% TR(q)
1
2
3
4
5
6
7

Na podstawie powyższej tabeli sporządź wykres funkcji ilustrujący zmianę wartości funkcji przychodu całkowitego, krańcowego i przeciętnego na skutek wzrostu wielkości sprzedaży

Czym może być spowodowany spadek wartości przychodu całkowitego, jeżeli wielkość sprzedaży przekroczy pewien poziom?

Ekonomia matematyczna I mgr inż. Piotr Betlej

Strona 1/6

---