Nr ćwiczenia: 104 |
Data: |
Imię i nazwisko: Garczyśki Oskar Gajewski Kamil |
Wydział Fizyki Technicznej |
Semestr: |
Grupa:
|
|
Prowadzący: |
Przygotowanie:
|
Wykonanie:
|
Ocena: |
|||
Temat ćwiczenia:
Podstawy teoretyczne
Rozchodzenie się dźwięku odbywa się w postaci fali mechanicznej i może mieć miejsce tylko w ośrodku sprężystym.
Jeżeli pewien element ośrodka, którego cząstki są ze sobą wzajemnie związane, pobudzimy do drgań, wówczas energia drgań tego elementu będzie przekazywana do punktów sąsiednich i wywoła w nich drgania.
Proces rozchodzenia się drgań nazywamy falą . Charakter fali rozchodzącej się w ośrodku zależy od jego właściwości sprężystych.
Najczęściej spotykanym ruchem drgającym jest ruch harmoniczny, w którym wychylenie y zmienia się w czasie t wg. równania:
gdzie: A-amplituda, ω-częstość kołowa, - faza początkowa
Faza początkowa określa stan ruchu w chwili t=0 i jest obierana w dowolny sposób. Jeżeli fala biegnie w kierunku osi x , wówczas kolejne punkty ośrodka pobudzane są do drgań i osiągają tę samą fazę z pewnym opóźnieniem. Prędkość przesuwania się wychylenia(zaburzenia)o stałej fazie jest prędkością rozchodzenia się fali.
Wychylenie y dowolnej cząstki w chwili t, w odległości x od źródła drgań opisane jest funkcją falową :
gdzie: ω- częstość kołowa ; - liczba falowa, - długość fali, - faza w punkcie x=0 i w chwili t=0.
Równanie fali jest podwójnie okresowe: względem czasu i przestrzeni. Przy ustalonej wartości x opisuje ono drgania cząstki wokół położenia równowagi - drgania te są periodyczne z okresem T. Ustalając w poprzednim równaniu czas otrzymujemy zależność wychylenia cząstek od ich położenia w określonej chwili - zależność ta przedstawia kształt fali. Odległość między najbliższymi punktami posiadającymi tę samą fazę nazywamy długością fali.
Związek między długością i okresem jest prędkością fali:
Prędkość fali w powietrzu
Ogólne wyrażenie określające prędkość rozchodzenia się fal podłużnych w ośrodku ciągłym ma postać:
gdzie: E- moduł Younga ośrodka, - jego gęstość.
Przekształcając podstawową postać prawa Hook'a możemy napisać:
(1)
gdzie oznaczają odpowiednio różniczkowe zmiany ciśnienia i objętości gazu o objętości V
Drgania dźwiękowe zachodzą tak szybko, że ściskanie i rozrzedzanie gazu można uważać za procesy adiabatyczne, wobec czego zmiana stanu gazu zachodzi zgodnie ze wzorem Poissona:
gdzie - jest stosunkiem ciepła właściwego przy stałym ciśnieniu do ciepła właściwego przy stałej objętości.
Różniczkując powyższy wzór otrzymujemy:
Podstawiając uzyskaną wartość do równania (2), a następnie uwzględniając otrzymaną w ten sposób postać modułu Younga w równaniu (1), wyrażamy prędkość fali podłużnej wzorem:
Stosując równanie stanu gazu doskonałego we wzorze na gęstość otrzymamy:
gdzie: n - ilość moli gazu, R - stała gazowa, T - temperatura.
n można wyrazić jako stosunek całej masy gazu m do masy 1 mola μ : n = m / μ.
Uwzględniają powyższe w ostatnim równaniu wstawiamy do równania (3) i otrzymujemy wzór określający prędkość dźwięku w zależności od rodzaju gazu i temperatury:
Aby obliczyć prędkość skorzystamy ze wzoru :
(3)
gdzie: λ - długość fali , f - jej częstotliwość
Wyniki pomiarów
Częstotliwość [Hz] |
Położenia mikrofonu |
|||||
553,3 |
66,4 |
|
|
|
|
|
885,5 |
42,7 |
80,8 |
|
|
|
|
1211 |
31,9 |
59,4 |
86,6 |
|
|
|
1556 |
25,6 |
47,4 |
69,2 |
|
|
|
1810 |
74,4 |
|
|
|
|
|
1937 |
44,3 |
86,2 |
|
|
|
|
2135 |
31,1 |
58,6 |
87 |
|
|
|
2665 |
21,1 |
38,9 |
55,4 |
72,9 |
89,9 |
|
2888 |
18,9 |
33,7 |
48,4 |
63,5 |
78,3 |
91,7 |
3210 |
16,3 |
28,8 |
42,1 |
56,1 |
68,7 |
80,8 |
Obliczenia
L.p. |
f [Hz] |
λ1 [cm] |
λ2 |
λ3 |
λ4 |
λ5 |
λ6 |
λŚr. |
1. |
553,3 |
62,4 |
|
|
|
|
|
62,4 |
2. |
885,5 |
38,7 |
38,1 |
|
|
|
|
38,4 |
3. |
1211 |
27,9 |
27,5 |
|
|
|
|
27,7 |
4. |
1556 |
21,6 |
21,8 |
21,8 |
|
|
|
21,7 |
5. |
1810 |
70,4 |
|
|
|
|
|
70,4 |
6. |
1937 |
40,3 |
41,9 |
|
|
|
|
41,1 |
7. |
2135 |
27,1 |
27,5 |
28,4 |
|
|
|
27,7 |
8. |
2665 |
17,1 |
17,8 |
16,5 |
17,5 |
17 |
|
17,2 |
9. |
2888 |
14,9 |
14,8 |
14,7 |
15,1 |
14,8 |
13,4 |
14,6 |
10. |
3210 |
12,3 |
12,5 |
13,3 |
14 |
12,6 |
12,1 |
12,8 |
Obliczanie wartości prędkości dźwięku [m/s]
v = λ ⋅ f= 345,2592
v = λ ⋅ f=340,032
v = λ ⋅ f=335,447
v = λ ⋅ f=337,652
v = λ ⋅ f= --- (prawdopodnie wystąpiły efekty dodatkowe)
v = λ ⋅ f=--- (prawdopodnie wystąpiły efekty dodatkowe)
v = λ ⋅ f=--- (prawdopodnie wystąpiły efekty dodatkowe)
v = λ ⋅ f=458,38
v = λ ⋅ f=421,648
v = λ ⋅ f=410,88
Średnia prędkość dźwięku:
380 ± 1,6 [m/s]
Obliczanie odchylenia standardowego średniej:
sqrt(1/(7-1)•((345.2592-378.47117)²+(340.032-378.47117)²+(335.447-378.47117)²+(337.652-378.47117)²+(458.38-378.47117)²+(421.648-378.47117)²+(410.88-378.47117)²)) =
=sqrt(1/6•((1103.03495)+(1477.56979)+(1851.0792)+(1666.20464)+(6385.42111)+(1864.23865)+(1050.33226))=
= sqrt(2566.31343) ≈ 50.65879
50.65879/2,6457513 ≈ 19,15
Prędkość dźwięku w temperaturze 20 stopni
![]()
Dane:
![]()
![]()
![]()
![]()
![]()
Dyskusja błędów
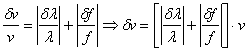
δf= 1 Hz
δλ=0,001 m
średnia λ=27,82857142857143 [cm] = 0,2782857142857143[ m]
średnia f=1852,6857 Hz
średnia v= 378,471 m/s
Wynik
δv= 1,565756452418613
Wnioski
W powietrzu, w temperaturze 20 °C, prędkość rozchodzenia się dźwięku jest równa 342,84 m/s. Obliczanie prędkości dźwięku z dwóch róznych wzorów (jeden w zależności od rodzaju gazu i temperatury , drugi w zależności od długości fali i częstotliwości) dowiodło,że wzory są prawidłowe , ponieważ wyniki niewiele różnią się od siebie.
Wyszukiwarka
Podobne podstrony:
przykłady sprawozdań, w. 7 - staarwnowagi do temp., Nr ćwiczenia
J POLSKI PRZYGOTOWANIE DO SPRAWDZIANU NR 2
J POLSKI PRZYGOTOWANIE DO SPRAWDZIANU NR 3
INFORMATYKA PRZYGOTOWANIE DO SPRAWDZIANU NR 2
INFORMATYKA PRZYGOTOWANIE DO SPRAWDZIANU NR 3
J POLSKI PRZYGOTOWANIE DO SPRAWDZIANU nr 4
Zagadnienia do sprawdzianu nr 1 z chemii
HISTORIA PRZYGOTOWANIE DO SPRAWDZIANU NR 4 XVIII W (OŚWIECENIE)
HISTORIA PRZYGOTOWANIE DO SPRAWDZIANU nr 1
HISTORIA PRZYGOTOWANIE DO SPRAWDZIANU nr 2
J NIEMIECKI PRZYGOTOWANIE DO SPRAWDZIANU NR 4
J NIEMIECKI PRZYGOTOWANIE DO SPRAWDZIANU NR 3
J NIEMIECKI PRZYGOTOWANIE DO SPRAWDZIANU NR 2
HISTORIA PRZYGOTOWANIE DO SPRAWDZIANU NR 3 XVII w
Zestaw treningowe nr 1 do sprawdzianu S1
Zestaw treningowe nr 2 do sprawdzianu S2, WNOŻCiK (moje studia), Semestr II, Chemia organiczna
ćwiczenia, Zagadnienia z wykładów do kolokwium nr 1, Chemia ćwiczenia, semestr letni 2009/2010
więcej podobnych podstron