ZAGADNIENIE 1

OPERATOR, RÓWNANIE WŁASNE, FUNKCJE I WARTOŚCI WŁASNE.

Operator - jest to odwzorowanie
gdzie X i Y są przestrzeniami wektorowymi nad tym samym ciałem K. (K jest ciałem liczb rzeczywistych).

Operator
jest liniowy gdy dla każdego a, b ∈K, x, y ∈X jest

Operator
jest hermitowski gdy:

Równaniem własnym operatora liniowego
nazywamy równanie postaci:

W równaniu tym funkcja ϕ_n spełniająca to równanie nazywa się funkcją własną operatora
(ϕ_n=e^{i λn x}), liczba λ_n nazywa się wartością własną operatora
zbiór {λ_n }nazywa się zbiorem wartości własnych operatora
, indeks n numeruje wartości własne, o ile są one dyskretne. Możliwe jest też, że widmo {λ} jest ciągłe. Można dowieść, że wartości własne operatorów hermitowskich są rzeczywiste.

ZAGADNIENIE 2

FUNKCJA STANU (FUNKCJA FALOWA), JEJ WŁASNOŚCI I SENS FIZYCZNY.

Postulaty mechaniki kwantowej stanowią podstawy formalne teorii fizycznej. Postulatów tych jest pięć, Jednym z nich jest właśnie funkcja stanu:

Postulat I

Każdemu układowi fizycznemu odpowiada funkcja stanu (funkcja falowa) zależna od współrzędnych przestrzennych i czasu, która jest ciągła wraz z pierwszymi pochodnymi w całym zakresie zmienności funkcji.

Komentarz:

Funkcja falowa (w układzie kartezjańskim Ψ=Ψ(x,y,z,t)) całkowicie określa stan układu fizycznego w mechanice kwantowej, układem tym może być elektron, atom , kryształ itd. Ogólnie jest to funkcja zespolona. Funkcja ta jest elementem przestrzeni Hilberta: Ψ∈X i opisuje falę materii.

Przestrzeń Hilberta jest to przestrzeń wektorowa (X,K,+,^. ), w której X jest zbiorem funkcji. K jest ciałem liczb rzeczywistych, + jest operacją dodawania elementów zbioru X, ^. jest operacją mnożenia wektora przez liczbę. Spełnione są wszystkie założenia typowe dla przestrzeni wektorowej, a ponadto:

1. dla dwóch dowolnych elementów u,v∈X można określić iloczyn skalarny:

gdzie całkowanie przebiega po całym zakresie zmienności u i v;

2. dla każdego u∈X określona jest norma:

;

c) przestrzeń Hilberta jest zupełna, czyli każdy ciąg Cauchy`ego funkcji, będących elementami przestrzeni Hilberta jest zbieżny do elementu należącego do tej przestrzeni.

Postulat II

Prawdopodobieństwo P znalezienia układu fizycznego opisywanego funkcją falową Ψ w elemencie przestrzeni dτ wynosi P=ΨΨ^*dτ=|Ψ|²dτ

Komentarz:

Prawdopodobieństwo P jest liczbą z przedziału [0,1].Dlatego, jeśli układ fizyczny może się znajdować tylko w obszarze Ω, tp żądamy, aby:

jest to warunek unormowania funkcji falowej. Spełnienie tego warunku wymaga aby:

lim_r∞ |Ψ(r,t)|² = 0

Zwróćmy uwagą, że bezpośrednią interpretację fizyczną ma właśnie kwadrat modułu funkcji falowej i ze względu na własności falowe obiektu określa on tylko prawdopodobieństwo znalezienia, a nie np. położenia obiektu jak w mechanice klasycznej.

ZAGADNIENIE 3

ZASADA ODPOWIEDNIOŚCI - OPERATORY POŁOŻENIA I PĘDU, ICH FUNKCJE WŁASNE I WARTOŚCI WŁASNE

Trzeci z postulatów mechaniki kwantowej opisuje zasadą odpowiedniości.

Postulat III

Każdej dynamicznej wielkości fizycznej F odpowiada liniowy operator hermitowski
, przy czym w wyniku pomiaru wielkości fizycznej F otrzymuje się tylko jedną z wartości własnych operatora
.

Komentarz:

Przedstawmy kilka operatorów, odpowiadających najważniejszym wielkościom dynamicznym:

pęd:

położenie

moment pędu

Widzimy, że niektóre operatory są operatorami różniczkowymi (gradient w operatorze pędu), inne polegają na mnożeniu przez liczbę (operator położenia). Operatory złożone konstruuje się na podstawie zależności analogicznych, jak w przypadku wielkości dynamicznych (operator momentu pędu).

Jak mówi postulat III, w wyniku pomiaru momentu pędu w badanym układzie fizycznym możemy otrzymać tylko jedną z wielkości własnych, czyli jedną z liczb ze zbioru {a_n}. W wyniku pomiarów mogą być tylko rzeczywiste i stąd żądanie hermitowskości operatorów wielkości dynamicznych.

Twierdzenie, że fizyka kwantowa przechodzi w fizykę klasyczną przy dużych liczbach kwantowych, nazywa się zasadą odpowiedniości. (wg Nielsa Bohra)

W zasadzie odpowiedniości Bohr wykazał, że pojęcia falowe i cząsteczkowe uzupełniają się, a nie przeciwstawiają

ZAGADNIENIE 4

KOMUTATOR DWÓCH OPERATORÓW, ZASADA NIEOZNACZONOŚCI.

Jeżeli spełnione jest równanie: [A, B] = AB - BA ≠ 0, to wtedy korzystamy z zasady nieoznaczoności.

Zasada nieoznaczoności - jest konsekwencją falowo-cząsteczkowej natury materii. Wynika z niepewności znajomości składowych pędu Δp_x, Δp_y , Δp_z i niepewności składowych położenia Δx, Δy, Δz podczas obliczeń współrzędnych elektronu podczas ugięcia wiązki elektronów na szczelinie. Iloczyn tych wielkości okazuje się wielkością stałą.

Wyraża się ją dla trzech składowych położenia elektronu:

Δp_x Δx ≥ h

Δp_y Δy ≥ h

Δp_z Δz ≥ h

gdzie:

h - jest stałą Plancka i wynosi h=6,25^.10^-34 J^.s

Nierówności te wyrażają zasadę nieoznaczoności Heisenberga w odniesieniu do położenia i pędu cząstki.

rys obrazujący ugięcie elektronów na szczelinie.

Zasada:

Iloczyn niepewności pomiaru pędu i pomiaru położenia cząstki jest zawsze nie mniejszy od stałej Plancka.

Zasada nieoznaczoności odnosi się do innych wielkości fizycznych. np. momentu pędu cząstki L i położenia kątowego ϑ ΔL Δϑ ≥ h, energii cząstki E i czasu t ΔE Δt ≥ h

O parach takich mówimy, że są kanonicznie sprzężone.

Uogólnienie:

Iloczyn niepewności pary wielkości fizycznych kanonicznie sprzężonych jest nie mniejszy od stałej Plancka. Niepewność ta nie jest zależna ani od metody pomiarowej, ani od dokładności przyrządów.

ZAGADNIENIE 5

RÓWNANIE SCHRODINGERA I JEGO ZNACZENIE, PRZYKŁADY.

Równanie Schrodingera jest równaniem ruchu w mechanice kwantowej. Jego rozwiązanie stanowi funkcja falowa
danego układu fizycznego, która całkowicie określa jego stan. Jest ona również bezpośrednio związana z falą materii rozpatrywanego układu. Z równania tego można znaleźć wartości własne energii układu.

Równanie Schrodingera składa się z sumy operatorów energii kinetycznej
i potencjalnej
. Operator energii kinetycznej w przypadku nierelatywistycznym ma postać
. Operator energii potencjalnej konstruuje się dla danego problemu fizycznego na podstawie zależności klasycznych.

Przykłady:

1 Cząstka swobodna

W przypadku cząstki swobodnej nie występują żadne zewnętrzne pola, więc
, stąd równanie przybiera najprostszą z możliwych postaci:

2 Oscylator harmoniczny

Energia potencjalna oscylatora harmonicznego w przypadku klasycznym ma postać V(x)=1/2kx², gdzie k oznacza stałą sprężystości. W związku z tym operator energii potencjalnej będzie miał postać
, a równanie Schrodingera dla atomu wodoru ma postać:

ZAGADNIENIE 7

CZĄSTKA SWOBODNA I JEJ FUNKCJA FALOWA

W mechanice kwantowej cząstce swobodnej przyporządkowana jest płaska monochromatyczna fala de Broglie'a. Dzięki temu prawdopodobieństwo znalezienia elektronu w danym punkcie przestrzeni jest niezależne od czasu. Biorąc dla prostoty tylko jedną z fal
, np. rozchodzącą się w dodatnim kierunku osi x, mamy:
.

Funkcja falowa cząstki swobodnej opisana jest równaniem:

, które możemy zapisać w postaci:
.

Funkcja falowa cząstki swobodnej jest falą płaską. Prawdopodobieństwo znalezienia cząstki swobodnej jest stałe i żadne miejsce w przestrzeni nie jest wyróżnione.

Prędkość cząstki swobodnej wynosi:
, a jej energia
.

ZAGADNIENIE 8

CZĄSTKA W JAMIE POTENCJAŁU, STANY ZWIĄZANE, DYSKRETNE WARTOŚCI ENERGETYCZNE.

Cząstka w nieskończenie głębokiej jamie potencjału.

Rozważamy tu cząstkę o masie m w potencjale, który w x<0 i x > a jest nieskończony, a w przedziale 0<x<a jest zerowy. Równanie Schrodingera w obszarze 0<x<a ma postać (potencjał zerowy):

a po wprowadzeniu oznaczenia:
. Równanie to można zapisać w postaci:
. Rozwiązaniem tego równania może być kombinacja liniowa funkcji rzeczywistych
, gdzie A i B są to pewne stałe.

Energie cząstki w nieskończenie głębokiej jamie potencjału są skwantowane i określone liczbą kwantową. Prawdopodobieństwo znalezienia cząstki w obszarze jamy potencjału zależy od energii cząstki: dla stanu podstawowego (n=1) jest ono maksymalne w środku jamy, a dla pierwszego stanu wzbudzonego (n=2) maleje w środku jamy do zera.

ZAGADNIENIE 10

OSCYLATOR HARMONICZNY, POZIOMY ENERGETYCZNE, DRGANIA ZEROWE.

Liniowym oscylatorem harmonicznym nazywamy cząstkę o masie m poruszającą się wzdłuż pewnej osi pod działaniem quasi - sprężystej siły F proporcjonalnej do wychylenia x cząstki z położenia równowagi : F= - kx. W wyrażeniu tym k jest współczynnikiem sprężystości związanym z masą cząstki m i kołową częstością własną
jej drgań zależnością :
. Energia potencjalna oscylatora harmonicznego ma postać U(x)=0,5*kx².

Poziomy energetyczne oscylatora harmonicznego:

Drgania zerowe - drgania występujące, dzięki istnieniu energii zerowej. Ich istnienie zostało potwierdzone doświadczalnie w zjawisku rozpraszania światła przez kryształy w bardzo niskich temperaturach. Dla T dążącego do 0 atomy zachowują pewne drgania zerowe, na których światło jest rozpraszane.

ZAGADNIENIE 12

SPIN ELEKTRONU, RZUT SPINU, LICZBY KWANTOWE, WARTOŚCI WŁASNE.

Spin elektronu - S - kręt, moment pędu spinowy; wewnętrzny moment pędu cząstek elementarnych i jąder atomowych, który w mechanice kwantowej jest własnością cząstek wynikającą z niezmienności względem obrotów. S=0,5

Kolejną wielkością jest spinowy moment magnetyczny elektronu. Ma on zawsze tę samą wartość
.

Liczby kwantowe - liczby przyjmujące zwykle wartości dyskretne - całkowite lub połówkowe, określające stany stacjonarne układu fizycznego. Odpowiedni ich układ służy do zdefiniowania układu lub oznaczenia możliwych stanów, w jakich dany układ może się znaleźć. Stan elektronu w atomie określa się czterema liczbami kwantowymi, które odpowiadają czterem stopniom swobody elektronu związanym z trzema współrzędnymi przestrzennymi i spinem.

Rzut spinu - wynosi
, gdzie h - stała Plancka

ZAGADNIENIE 13

FERMIONY, BOZONY I ZAKAZ PAULIEGO

Fermiony - cząstka lub quasi - cząstka podlegająca statystyce Fermiego - Diraca. Funkcja falowa opisująca wielocząsteczkowy stan identycznych fermionów jest antysymetryczna przy zmianie dwóch cząstek. Elementarne fermiony to: elektron, mion, neutrino, nukleony oraz ich antycząstki.

Bozony - cząstka lub quasi - cząstka podlegająca statystyce Bosego - Einsteina. Funkcja falowa opisująca wielocząsteczkowy stan identycznych bozonów jest symetryczna przy zamianie dwóch cząstek. Wszystkie bozony mają spin całkowity. Elementarne bozony: fotony i mezony.

Zakaz Pauliego - zasada Pauliego - układ elektronów może znajdować się wyłącznie w stanie, w którym każdy z elektronów obsadza inny stan kwantowy. W teorii pól kwantowych zasada ta wyraża fakt, że fermiony mogą obsadzać dozwolone im stany tylko pojedynczo. Funkcje falowe układu fermionów musza być całkowicie antysymetryczne ze względu na permutacje cząstek.

ZAGADNIENIE 15

OPIS CZĄSTECZKI, PRZYBLIŻENIE PÓŁKLASYCZNE I PRZYBLIŻENIE BORNA - OPPENHEIMERA

Przybliżenie półklasyczne - jest to przybliżenie, w którym jądra traktuje się klasycznie, a elektrony kwantowo.

Przybliżenie klasyczne jest niewątpliwie podejściem bardzo wygodnym. Wyobrażamy sobie bowiem cząsteczkę

Jako układ punktowych jąder, z których każde wytwarza potencjał kolumbowski Ze/4πε₀│r-R_n│, a w polu wytwarzanym przez te jądra poruszają się elektrony, które możemy traktować jako rozmytą chmurę ładunku. Możliwość zastosowania takiego przybliżenia opiera się na tym, że masa jądra jest znacznie (zwykle wiele tysięcy razy) większa od masy elektronów, więc falowa natura jąder jest „mniej widoczna”.

Cząstka chemiczna w stanie podstawowym - w powyższym przybliżeniu - jest tworem, w którym układ jąder i kształt chmury elektronowej jest taki, że:

Elektrony znajdują się w pewnym stacjonarnym (wieloelektronowym) stanie własnym, odpowiadającym potencjałowi wytwarzanemu przez jądra.

Siła działająca na każde z jąder jest równa 0.

Łatwo sobie wyobrazić, że rozwiązanie, choćby nawet tylko przybliżone, takiego problemu fizycznego jest bardzo skomplikowane. Trzeba bowiem znaleźć energię najmniejszą zarówno ze względu na rozłożenie „klasycznych” jąder, jak i „kwantowych” elektronów.

Przybliżenie Borna - Oppenheimera

Rozpatrujemy dwa jądra A i B. Jeżeli przypuścimy, że dostatecznie powolnym ruchem jądro B przesunęło się o mały wektor ΔR_B, co widać na rysunku. Praca wykonana przy tym (dodatnia lub ujemna) musi się składać z dwóch części.:

- zmiany energii elektrostatycznego odpychania jąder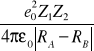
- przy oddalaniu się jąder zewnętrzna praca ma znak ujemny,

- zmiany energii chmury elektronowej układu, w tym zarówno średniego oddziaływania elektron - jądro, jak i elektron - elektron. Energię chmury elektronowej układu oznaczamy: E_e(R_B-R_a). Ze względu na symetrię przestrzeni energia ta dla dwóch jąder może zależeć tylko od modułu odległości │R_B-R_A│. W zależności od odległości między jądrami i stanu elektronowego zmiana E_e przy oddalaniu się może być dodatnia lub ujemna.

Całkowita wykonana praca musi być równa sumie obu zmian energii, a więc zmianie wielkości

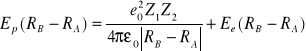
E_p może być potraktowane jako efektywna energia potencjalna oddziaływania jądro - jądro w cząsteczce chemicznej. Przyjęcie istnienia efektywnej energii potencjalnej w postaci, wzór jak powyżej, nazywamy przybliżeniem Borna - Oppenheimera. Przybliżenie to stanowi podstawę bardzo wielu rozważań zarówno w fizyce cząsteczkowej, jak i w fizyce ciała stałego. Przybliżenie to możemy zastosować np. do jednokrotnie zjonizowanej cząsteczki wodoru.

ZAGADNIENIE 16

RODZAJE WIĄZAŃ W CZĄSTECZKACH I ICH WŁASNOŚCI.

Wiązania chemiczne - jeżeli atomy obojętne elektrycznie znajdujące się w dużej odległości zbliżone na pewną odległość, poprzez wzajemne siły oddziaływania przyciągającego utworzą cząsteczkę mówimy o powstania wiązania chemicznego. Siły powodujące utworzenie wiązania chemicznego są siłami pochodzenia elektrycznego.

W cząsteczkach takich występują głównie dwa rodzaje wiązań:

1. Wiązania jonowe (heteropolarne)

2. Wiązania kowalentne (homeopolarne) zwane walencyjnymi.

Zaznaczyć jednak trzeba, że wiązania jonowe i kowalentne nie są jedynymi rodzajami wiązań występujących w cząsteczkach. Spotyka się wiązania, które maja charakter pośredni, szczególnie widoczne jest to w ciałach stałych (tzw. wiązanie metaliczne).

Wiązanie jonowe - powstaje w wyniku dążenia do zapewnienia zewnętrznej ośmioelektronowej powłoki w atomie. Atomy które mają w zewnętrznej podpowłoce więcej niż cztery elektrony łatwo przyłączają dodatkowe elektrony. Takie atomy nazywa się atomami elektroujemnymi. Natomiast atomy posiadające w zewnętrznej podpowłoce mniej niż pięć elektronów łatwo pozbywają się tych elektronów. Atomy takie nazywamy elektrododatnimi. Trwałość zapełnionej podpowłoki tłumaczy się tym, że przy obsadzaniu wszystkich ośmiu stanów w podpowłoce orbitalne i spinowe momenty elektronów są wzajemnie skompensowane. Przy zbliżaniu atomu elektroujemnego i atomu elektrododatniego, jeden atom oddaje elektron (lub elektrony) drugiemu i przekształca się w jon dodatni, drugi zaś przekształca ten elektron (elektrony) i staje się jonem ujemnym. Między jonami działają siły kulombowskie przyciągania, powodujące powstanie cząsteczki o wiązaniu jonowym.

Cechy wiązań jonowych:

• siły oddziaływania są siłami kulombowskimi,

• w węzłach sieci krystalicznej tych kryształów są rozmieszczone zwykle na przemian dodatnie i ujemne jony.

Wiązania kowalentne - występują w cząsteczkach złożonych z jednakowych atomów (H₂, O₂, N₂ itp.). Wiązania kowalentne spotyka się również we wszystkich organicznych i wielu nieorganicznych związkach. Wiązanie to można wyjaśnić tym, że w pewnych warunkach prawdopodobieństwo przebywania w obszarze między atomami dwóch elektronów (po jednym z każdego atomu) jest bardzo duże. W tym obszarze wytwarza się chmura ładunku ujemnego, natomiast w pozostałych obszarach w pobliżu jąder występują chmury ładunku dodatniego. Między obszarem środkowym, a pozostałymi obszarami działają siły oddziaływania kulombowskiego, realizujące wiązanie cząsteczki.

Cecha wiązania kowalentnego jest to, że jest ono utworzone zawsze przez dwa elektrony, które tworzą parę wspólną obu atomów. Następuje ciągła wymiana elektronów, stad siły wiązania kowalentnego nazywane są często siłami wymiennymi.

ZAGADNIENIE 18

WIDMA ROTACYJNE I OSCYLACYJNO - ROTACYJNE

Przejściami czysto rotacyjnymi nazywamy przejścia ze stanów o różnym l, ale o tym samym v (np. v=0 ). Przejścia takie obserwuje się w bardzo dalekiej podczerwieni lub nawet w mikrofalach. Stanowią one z dobrym przybliżeniem układ linii równo oddalonych od siebie w skali energii.

Układ linii widmowych przejścia rotacyjnego w funkcji energii fotonów.

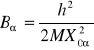
ZAGADNIENIE 19

WIDMA CZĄSTECZKOWE, ELEKTRONOWO-ROTACYJNO-OSCYLACYJNE - WIDMO PASMOWE.

Nie posiadamy więcej wiadomości!!!

ZAGADNIENIE 20

RODZAJE CIAŁ STAŁYCH - POLIKRYSZTAŁY, MONOKRYSZTAŁY I CIAŁA BEZPOSTACIOWE.

Monokryształ - ciało, które jest w całości pojedynczym kryształem charakteryzującym się jednolitą strukturą wewnętrzną o określonej symetrii(regularny kształt zewnętrzny).Ciała monokrystaliczne mają zwykle płaskie ściany i proste krawędzie usytuowane pod określonymi kątami Monokryształy wykazują anizotropowość swoich własności fizycznych (własności ciał zależą od kierunku). Monokryształy naturalne mają wiele przypadkowych zanieczyszczeń i dlatego nie nadają się do większości badań i zastosowań. Zwykle do celów badawczych i do zastosowań monokryształy otrzymuje się sztucznie w określonych warunkach, stosując specjalne urządzenia.

Polikryształ - ciało stałe składające się z licznych małych kryształków zrośniętych przypadkowo pod różnymi orientacjami kierunków krystalograficznych. Dlatego własności ciał polikrystalicznych są jednakowe we wszystkich kierunkach. Mówimy, że są to ciała izotropowe. Większość spotykanych na co dzień ciał stałych jak np. kamienie, minerały, metale itp. , to polikryształy. Jeżeli powierzchnię polikryształu oszlifujemy i wytrawimy w odpowiedniej substancji chemicznej, to pod mikroskopem zauważymy, że ciało takie składa się z wielu oddzielnych ziaren krystalicznych, o przypadkowym kształcie, spowodowanym swobodnym wzrostem każdego kryształka ograniczanym przez inne ziarna krystaliczne.

Ciała bezpostaciowe - ciała nie wykazujące żadnych regularnych płaszczyzn ograniczających, nie można w nich ustalić jakiegokolwiek prawidłowego ułożenia cząstek, a każdy kierunek jest równoważny pod względem własności fizycznych. Możemy do nich zaliczyć m.in.: szkła, żywice, tłuszcze, niektóre proszki.

ZAGADNIENIE 21

SIŁY ODDZIAŁYWANIA W CIAŁACH STAŁYCH - RODZAJE WIĄZAŃ, WIĄZANIA JONOWE.

Przyczyną istnienia wiązań jonowych jest fakt, że elektrony w atomie są związane silniej wtedy, gdy tworzą zamkniętą powłokę elektronową, następne elektrony rozpoczynające zabudowę kolejnej powłoki są związane słabiej. Wobec czego może się zdarzyć, że przy zbliżeniu dwóch różnych atomów, z których jeden ma nadmiar elektronów zewnętrznych (poza zapełnioną całkowicie powłoką elektronową), a drugiemu brakuje akurat tyle elektronów do całkowitego zapełnienia swojej powłoki elektronowej, że elektrony zewnętrzne, słabiej związane w atomie pierwszym przejdą do atomu drugiego. Powstaną wtedy dwa jony - jeden dodatni, drugi ujemny. Dzięki kolumbowskiemu przyciąganiu się tych dwóch różnoimiennych jonów powstanie cząsteczka chemiczna o tzw. wiązaniu jonowym. W krysztale jonowym jony dodatnie ułożone są przemiennie z jonami ujemnymi.

Typowym przykładem kryształu jonowego jest kryształ soli NaCl (Na⁺ Cl ^-). Obojętny atom sodu Na ma 11 elektronów, które zapełniają całkowicie powłoki elektronowe K i L. W zewnętrznej powłoce M ma tylko jeden elektron słabo związany. Atom chloru Cl ma 17 elektronów, a do zapełnienia podpowłoki brakuje mu właśnie jednego elektronu. Atom chloru przy zbliżeniu z atomem sodu pobiera od niego brakujący elektron. Powstają w ten sposób dwa jony -Na⁺ i Cl^-, które przyciągając się tworzą cząsteczkę NaCl.

ZAGADNIENIE 22

SIŁY ODDZIAŁYWANIA W CIAŁACH STAŁYCH - RODZAJE WIĄZAŃ, WIĄZANIA KOWALENCYJNE.

Wiązania kowalencyjne występują między atomami obojętnymi. Charakteryzują się tym, że atomy tworzące cząsteczkę lub kryształ mają wspólne elektrony - po dwa zlokalizowane elektrony przypadające na dwa atomy biorące udział w wiązaniu. Każdy atom może utworzyć ograniczoną liczbę wiązań kowalencyjnych. Każde wiązanie jest utworzone przez parę elektronów mających przeciwnie ustawione spiny. Elektrony tworzące wiązanie mogą się poruszać w przestrzeni określonej wspólną funkcją falową utworzona z funkcji falowych obu elektronów.

Jak wiemy, orbitale elektronowe s są kuliście symetryczne, natomiast orbitale typu p, d, f itd. mają „wypustki” usytuowane w określonych kierunkach w przestrzeni. Dlatego wiązania kowalencyjne utworzone z tych ostatnich orbitali będą usytuowane pod określonymi kątami. Zatem atomy będą umieszczone pod odpowiednimi kątami wynikającymi z kształtu wypadkowych orbitali tworzących wiązania kowalencyjne.

Jeżeli w krysztale każdy atom tworzy z każdym ze swoich sąsiadów wiązanie kowalencyjne, to taki kryształ stanowi jak gdyby jedną ogromną cząsteczkę. Silne wiązania każdego atomu ze swoimi sąsiadami powodują, że kryształy kowalencyjne są zwykle bardzo twarde, charakteryzują się wysoką temperaturą topnienia oraz dużym ciepłem topnienia. Przykładem kryształu kowalencyjnego jest diament i karborund (SiC).

ZAGADNIENIE 24

STRUKTURA KRYSZTAŁU O WIĄZANIU JONOWYM I METALICZNYM - MODEL CIASNO UPAKOWANYCH KUL.

Wiązanie jonowe

Omówmy cząsteczkę KCl. W najbliższym sąsiedztwie każdego jonu znajduje się zatem 6 jonów innego rodzaju, które działają na dany jon siłami przyciągania oraz 12 jonów tego samego rodzaju w sąsiedztwie nieco dalszym, które na dany jon działają siłami odpychania. Zarówno jony Cl^- jak i z osobna jony K⁺ tworzą strukturę krystaliczną regularną centrowaną płasko, zaś kryształ KCl jest nałożeniem się obu sieci Bravaise'go.

Wiązanie metaliczne.

Oddziaływanie dodatnich jonów metalu z gazem swobodnych elektronów jest przyczyną powstawania siły przyciągania między jonami metali i stanowi istotę wiązania metalicznego. Elektrony swobodne znajdujące się między jonami metalu powodują zbliżenie tych ostatnich, ponieważ zmniejszają siły odpychania występujące między jednakowo naładowanymi jonami. W miarę zmniejszania się odległości między jonami rośnie gęstość elektronów swobodnych, przez co rośnie siła przyciągania wywołana oddziaływaniem gazu elektronowego z jonami dodatnimi metalu. Wiązania metaliczne występują dla pierwiastków, które mają mało elektronów walencyjnych w atomie.

Struktura najgęstszego upakowania kul: Gdy kationy są dostatecznie małe, to aniony niemal stykają się ze sobą, a kationy zajmują położenie w lukach między anionami. Zatem całą sieć krystaliczną można utworzyć ze stykających się ciasno upakowanych kul anionów, wstawiając w odpowiednie luki między tymi kulami mniejsze kuleczki - kationy.

Sposób ustawiania: Pojedynczą warstwę można ułożyć tylko w jeden sposób tak, że każda kula otoczona będzie przez sześć sąsiednich. Następną warstwę trzeba kłaść tak, aby kule umieszczać w zagłębienia warstwy pierwszej. Nie można zapełniać wszystkich zagłębień kulami o tych samych rozmiarach. Kule będą zajmować co drugie zagłębienie. Ułożenie gęste dwóch warstw może być przeprowadzone też tylko w jeden sposób. Różnica wystąpi dopiero przy kładzeniu warstwy trzeciej. Można położyć ją dwojako: tak, aby środki kul leżały nad środkami kul warstwy pierwszej lub tak, aby środki kul nie pokrywały się ze środkami kul warstwy pierwszej. Stąd można struktury takie zapisać za pomocą kodu ABABAB... lub ABCABCABC... Okazuje się, że w strukturze o ułożeniu warstw ABAB... można wyodrębnić komórkę heksagonalną, natomiast w strukturze ABCABC... można wyodrębnić komórkę regularną, powierzchniowo centrowaną. W strukturach najgęstszego upakowania kul występują dwa rodzaje luk między kulami: jedne z nich otoczone są czterema kulami, których środki tworzą wierzchołki regularnego tetraedru, drugie otoczone są sześcioma kulami, których środki tworzą wierzchołki oktaedru. W lukach umieszczone są mniejsze kuleczki - kationy. Luki mogą być zapełnione w różny sposób - prowadzi to do większego urozmaicenia struktur kryształów jonowych. Jeżeli kationy mają nieco większe rozmiary niż odpowiednie luki to nie mieszczą się tam i rozsuwają od siebie większe kule anionów powodując rozluźnianie gęstego upakowania kul.

Model ciasno upakowanych kul jest bardzo użyteczny, gdyż pozwala objaśnić nie tylko struktury kryształów o wiązaniach jonowego ale również wiele kryształów metalicznych. Kryształy o wiązaniach metalicznych zbudowane są z dodatnich jonów, między którymi istnieje gaz elektronowy. Formalnie wiele takich struktur można rozpatrywać jako konstrukcje ciasno upakowanych kul. Model ciasno upakowanych kul nie da się jednak zastosować do kryształów kowalencyjnych. Wiązania kowalencyjne są utworzone dzięki częściowemu pokrywaniu się orbitali sąsiednich atomów. Orbitale te, za wyjątkiem orbitali s, mają określoną kierunkowość. Kierunkowe własności orbitali mają decydujący wpływ na charakter struktur kowalencyjnych

ZAGADNIENIE 25

KRYSZTAŁY METALI I PÓŁPRZEWODNIKÓW - PRZYBLIŻENIE JEDNOELEKTRONOWE.

Przybliżenie jednoelektronowe - polega na tym, że zamiast rozpatrywać oddziaływanie danego elektronu z każdym z pozostałych elektronów walencyjnych, w sieci przestrzennej, przyjmiemy, że rozpatrywany elektron porusza się w pewnym polu wypadkowym, wytwarzanym przez wszystkie jądra atomowe i wszystkie pozostałe elektrony.

Zakładamy przy tym, że potencjał tego pola, zwany potencjałem efektywnym jest niezależny od czasu. Dodatkowo przyjmujemy, że rdzenie atomowe stanowiące osnowę kryształu, są nieruchome i tworzą idealnie uporządkowaną sieć przestrzenną

Struktura krystaliczna

Metale - jądra i elektrony powłok traktujemy jako nierozdzielne jony zwane (rdzeniami atomowymi). Kiedy atomy tworzą kryształ wzajemne oddziaływanie wszystkich elektronów i jonów powoduje, że elektrony odrywają się od rdzeni macierzystych i zaczynają się swobodnie poruszać. Pomiędzy dodatnimi jonami istnieje wzajemne odpychanie, a wiec budowa kryształu powinna być taka aby odległości pomiędzy jonami były jak największe. Podstawowe struktury tego typu to kubiczna (fec) i heksagonalna (hop). Różnica pomiędzy strukturami fec i hop polega na odmiennym ułożeniu kul na sobie. Większość metali krystalizuje w jednej z tych dwóch struktur.

Z mikroskopowej budowy metali wynika wiele właściwości makroskopowych np. kowalność metalu (deformacja plastyczna) wynika z mało ścisłych wiązań pomiędzy jonami dzięki czemu możemy je łatwo przesuwać nie krusząc metalu. Z istnieniem w metalach prawie swobodnych elektronów związane jest przewodnictwo elektryczne.

Półprzewodniki - elektrony walencyjne są uwspólnione i mogą się prawie swobodnie poruszać w półprzewodnikach na skutek istnienia przerwy energetycznej pomiędzy pasmem walencyjnym, a przewodnictwa liczba nośników swobodnych jest bardzo silnie uzależniona od czynników zewnętrznych (np. temp.). Liczba nośników swobodnych w półprzewodnikach jest kilka rzędów wielkości mniejsza niż w typowych metalach.

W czystym półprzewodniku w pasmach pustych nie ma elektronów natomiast całkowicie zapełnionych są elektrony ale prąd w nich zanika (w temp. 0 bezwzględnego). W temp. Skończonych istnieje różne od zera prawdopodobieństwo przerzucenia elektronu z pasma walencyjnego do przewodzenia w niezerowej temp. istnieje pewna liczba dziur i elektronów, istnieją więc nośniki swobodne. Liczba ich rośnie z temperaturą. Liczbę nośników swobodnych w jednostce objętości nazywamy koncentracją.

Pasma i poziomy energetyczne w półprzewodniku.

Przybliżenie jedno-elektronowe - ze względu na ogromną liczbę elektronów swobodnych przy opisie metali najczęściej posługujemy się przybliżeniem Hartree'ego (jednoelektronowym).

Poszukujemy rozw. W postaci iloczynu

Ψ(r₁,r₂,...,r_n)=Ψ₁(r₁)Ψ₂(r₂)...Ψ_n(r_n)

Każda z funkcji Ψ_n ma spełniać jednoelektronowe równanie Schroedingera:

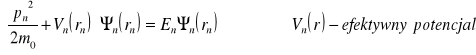
W idealnym krysztale V_n(r) jest (z dużą dokładnością) potencjałem periodycznym z okresem sieci.

Potencjał V(r) wytworzony przez wszystkie jądra i elektrony ma pełną symetrię sieci. Ma więc symetrię translacyjną bo jest periodyczny. Ma także wszystkie symetrie punktowe.

ZAGADNIENIE 26

MODEL PRAWIE SWOBODNYCH ELEKTRONÓW, TWIERDZENIE BLOCHA, FUNKCJA BLOCHA.

WERSJA 1

Twierdzenie Blocha - struny elektronowe w idealnym krysztale można wyznaczyć rozwiązując równanie Schroedingera.

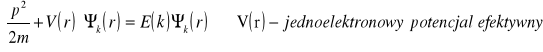
Potencjał V(r) charakteryzuje się symetrią sieci

R_n=n₁a₁+n₂a₂+n₃a₃

Wektory a_i są wektorami podstawowymi sieci prostej, zaś n_i są liczbami całkowitymi.

Zgodnie z tw. Blocha każdy stan elektronowy w krysztale jest scharakteryzowany przez wektor falowy k. Funkcja falowa elektronu stanowi zmodulowaną falę płaską z modulacją określoną za pomocą sieci krystalograficznej. Funkcja ta może mieć postać:

u_k(r) - wykazuje symetrię sieci krystalograficznej

W przypadku jednowymiarowym

Funkcję tej postaci nazywamy funkcją Blocha. Funkcja Blocha daje gęstość prawdopodobieństwa elektronu periodyczną z okresem sieci (mimo, że sama nie jest periodyczna z tym okresem)

u_k(x) nie jest periodyczne z okresem sieci

WERSJA 2

Twierdzenie Blocha.

Funkcje falowe elektronów w krysztale opisywane są funkcją Blocha.

Funkcja Blocha.

Ruch elektronu swobodnego w okresowym polu kryształu opisuje pewne równanie Schrodingera, które jak udowodnił Bloch ma rozwiązanie w postaci następującej funkcji:
, będącej iloczynem funkcji dla biegnącej fali płaskiej
opisującej ruch elektronu swobodnego w polu o stałym potencjale i funkcji okresowej u(x) zależnej od liczby falowej k i mającej ten sam okres d co energia potencjalna U(x), tzn.:

U(x)=U(x + d), u(x) = u(x + d), d = a + b. Funkcje
nazywają się funkcjami Blocha. Przy odpowiednio dobranej funkcji u_k(x), funkcje Blocha mogą być rozwiązaniem dowolnego zagadnienia potencjalnego.

ZAGADNIENIE 28

WARUNKI BRZEGOWE W SKOŃCZONYM KRYSZTALE, DYSKRETNE POZIOMY ENERGETYCZNE.

Nałożenie warunków brzegowych jest równoważne założeniu, że cały nieskończony kryształ jest zbudowany z makroskopowych segmentów, powtarzających się okresowo w przestrzeni. Każdy z nich jest równoważny badanemu kryształowi rzeczywistemu. Pomijamy w warunkach brzegowych zjawiska powierzchniowe.

Tak więc dla dowolnej wielkości fizycznej zamiast rozpatrywać cały kryształ możemy rozpatrywać jedynie jego jeden segment.

Na ogół wprowadza się sztuczne warunki brzegowe, aby przejść od nieskończonej do skończonej liczby stanów.

Wyodrębniając pewien obszar w krysztale, np. sześcian o boku L

Żądamy, aby każdą możliwą funkcja falowa można opisać równaniem:

Ψ(x+L,y,z)=Ψ(x,y+L,z)=Ψ(x,y,z+L)=Ψ(x,y,z)

Dopuszczamy więc tylko takie funkcje Blocha, że spełnione są funkcje:

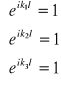
czyli k_i=n_i ^. 2π / L

Dozwolone energie E elektronów w krysztale są funkcjami wektora falowego k.

Nałożenie warunków brzegowych oznacza nałożenie na k pewnych warunków.

W rezultacie dla kryształu z nałożonymi warunkami wektory falowe k mogą przyjmować tylko dyskretne wartości tak więc dozwolone energie elektronów w krysztale stają się funkcjami dyskretnego wektora falowego.

Dokładniejsza analiza wskazuje, że wieloznaczną funkcję E(k) określoną w całej przestrzeni wektora k można traktować jako zespół jednoznacznych funkcji ciągłych E_n(k) określonych dla k z pierwszej strefy Brillouina, numerowanych parametrem n (n∈N).

Mówimy, że parametr n numeruje pasma energetyczne.

ZAGADNIENIE 29

PASMA ENERGETYCZNE, ZAKAZ PAULIEGO, PODZIAŁ NA METALE I PÓŁPRZEWODNIKI.

Zakaz Pauliego: W określonym stanie kwantowym scharakteryzowanym kompletem czterech liczb kwantowych może znajdować się nie więcej niż 1 elektron.

Daje to taki efekt, że w temp. 0K stany o najniższych energiach obsadzone są całkowicie (po 2 elektron y na stan, licząc degradację spinową), inne są całkowicie puste.

Metale - należą do grupy mającej najwyższe pasmo energetyczne zawierające elektrony nie całkowicie zapełnione. Wewnątrz tego pasma elektrony mogą być łatwo wzbudzone, podniesione na wyższe poziomy energetyczne.

Ppółprzewodniki - ciała, w którym nad pasmem zapełnionym całkowicie leży pasmo puste oddzielone przerwą energetyczna. Gdy przerwa energetyczna jest dostatecznie mała, to w zwykłych temperaturach na skutek wzburzeń termicznych część elektronów może przejść do pasma przewodnictwa. Wówczas przez przyłożenie zewnętrznego pola elektrycznego łatwo wywołać przepływ prądu. (w temp 0K półprzewodniki nie przewodzą

przewodnik półprzewodnik

Pasma energetyczne - są to pasma o określonej energii elektronów. Opisane są za pomocą wektora falowego k i parametru n numerującego pasma energetyczne (czyli poszczególne gałęzie E(k)), opisane są one również przy pomocy stref Brillouina.

Różnice pomiędzy kolejnymi poziomami energetycznymi w paśmie są rzędu 10^-23aV.

W temp. 0K najwyższe pasmo zawierające elektrony nazywamy pasmem walencyjnym, a pasmo leżące nad nim pasmem przewodzenia, rozróżnia się również pasma energii wzbronionych. W zależności od obsadzenia i wzajemnego położenia pasm oraz os swobody ruchu elektronów ciała dzielimy jak wyżej.

ZAGADNIENIE 30

DYNAMIKA ELEKTRONÓW W CIELE STAŁYM, DZIURY I ICH WŁASNOŚCI.

Dziura - quasi- cząstka służąca do opisu własności fizycznych zapełnionego pasma energetycznego w krysztale, z którego zabrano jeden elektron. Ma ona ładunek dodatni. Masa efektywna dziury w pasmie walencyjnym z reguły jest większa niż masa efektywna elektronu w pasmie przewodnictwa. Dziury są nośnikami prądu i jeśli decydują o przewodnictwie elektrycznym kryształu, to mówi się, że półprzewodnik jest typu p. Ruchliwość dziur zwykle jest mniejsza niż ruchliwość elektronów. Dziurze możemy przypisać : prędkość, pseudopęd (dziura ma opisać stan kryształu z prawie zapełnionym pasmem walencyjnym, musimy jej więc przypisać całkowity pseudopęd układu wszystkich elektronów w tym pasmie.

ZAGADNIENIE 31

PÓŁPRZEWODNIKI SAMOISTNE, KONCENTRACJA NOŚNIKÓW, ZALEŻNOŚĆ PRZEWODNICTWA OD TEMPERATURY

Półprzewodniki samoistne - czyste półprzewodniki (German, Krzem) w budowie idealnej każdy atom przez swoje elektrony walencyjne wiąże 4 sąsiednie atomy. Struktura elektrycznie obojętna (po zwiększeniu temperatury - dostarczeniu energii zwiększa się energia, elektrony przechodzą do pasma przewodnictwa, ale pozostają po nich dziury (ładunki +). Inna definicja półprzewodników samoistnych mówi, że są to półprzewodniki, w których praktycznie wszystkie nośniki swobodne pochodzą z przejść międzypasmowych. Liczba nośników w jednostce objętości określana jest jako koncentracja nośników. W półprzewodniku samoistnym koncentracja elektronów jest równa koncentracji dziur, czyli n = p.

Zależność liczby nośników w półprzewodniku samoistnym od temperatury określa się wzorem:

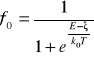
gdzie:

- stała Boltzmana

- energia Fermiego (wielkość charakterystyczna dla rozkładu)

Rozkład Fermiego - Diraca

ZAGADNIENIE 32

DYFUZJA NOŚNIKÓW.

Dyfuzja - przemieszczanie się nośników prądu w półprzewodniku pod wpływem istnienia gradientu ich koncentracji. Gradient koncentracji może być wywołany różnicą temperatur lub oświetleniem lokalnym. Dyfuzja nośników prądu zachodzi również na styku dwu ciał różniących się energią Fermiego (na styku dwu metali lub złączy p-n).

W ruchu dyfuzyjnym nośników swobodnych w półprzewodnikach oddziaływanie zachodzi przede wszystkim z zakłóceniami idealnej periodyczności sieci krystalicznej, a więc np. z domieszkami, drganiami sieci krystalicznej itp. Jeżeli koncentracja nośników (stężenie) jest stała, wtedy dyfuzja nie prowadzi do żadnych zmian. Czysty proces dyfuzyjny określony jest równaniem:

ZAGADNIENIE 33

GENERACJA I REKOMBINACJA NOŚNIKÓW W PÓŁPRZEWODNIKACH, RÓWNOWAGA TERMODYNAMICZNA.

Generacja - powstawanie nośników swobodnych w półprzewodniku. Generacja może być różnego rodzaju. Może polegać np. na powstawaniu par elektron - dziura, czyli na przejściach międzypasmowych - taki proces jest analogiczny do kreacji elektron - pozyton. Może być związana z jonizacją domieszek itp. Generację mogą wywoływać także bombardowanie kryształu szybkimi elektronami.

Rekombinacja - zanikanie nośników swobodnych w półprzewodniku. Może być związana np. ze zanikaniem par elektron - dziura w procesie analogicznym do anihilacji par elektron - pozyton, czyli nie używając pojęcia dziury - z powrotem elektronu z pasma przewodnictwa do pasma walencyjnego. Może ona polegać na wychwytywaniu elektronów czy dziur z pasm domieszki i inne defekty struktury itp.

Równowaga termodynamiczna - warunki, w których procesy rekombinacji musza przebiegać z tą samą prędkością co procesy generacji, bo liczba nośników nie może zależeć od czasu. Dla równowagi termodynamicznej słuszne są wyrażenia:

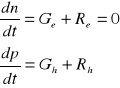
i słuszna jest relacja, wynikająca z powyższych wyrażeń:

gdzie:

G_e0 - generacja nośników

n₀, p₀ - liczba elektronów i dziur w warunkach równowagi termodynamicznej.

ZAGADNIENIE 34

PLAZMA I JEJ WŁASNOŚCI, DRGANIA PLAZMOWE, PLAZMONY.

Plazma - zjonizowany gaz będący quasi obojętną mieszaniną cząstek obojętnych oraz jonów dodatnich i swobodnych elektronów. Liczba ładunków dodatnich i ujemnych jest taka sama, jednak w bardzo małych obszarach i krótkich czasach mogą wystąpić zakłócenie obojętności. Plazma jest nazywana czwartym stanem skupienia.

Plazma jest to ośrodek, w którym istnieją swobodne nośniki prądu elektrycznego. Można mieć do czynienia z plazmą gazową, ciekłą, w ciele stałym, w metalach i półprzewodnikach. Własności plazmy: jakiekolwiek zgęszczenie czy rozrzedzenie ładunku powoduje powstanie drgań własnych układu, z tak zwaną częstością plazmową. Wyjaśnienie zjawiska drgania w plaźmie: W jakimś miejscu plazmy zgromadziliśmy pewną ilość ładunków swobodnych. Wtedy te ładunki będą się odpychać i rozbiegać na wszystkie strony. Na skutek bezwładności nośników ich ruch będzie się odbywał dalej i powstające tu pole elektryczne zatrzyma poruszające się ładunki (w miejscu dawnego zagęszczenia nastąpi rozrzedzenie). Teraz ładunki swobodne zaczną zbiegać się w kierunku rozrzedzenia. A zatem pojawią się w układzie drgania plazmowe. Drgania te mają częstość niezależną od długości fali. Częstość plazmowa zależy od koncentracji nośników w potędze 0.5. Powinna więc być znacznie większa dla metali niż dla półprzewodników. Plazma jest elektrycznie obojętna, a zatem w nieobecności pola elektrycznego lub magnetycznego nie ma żadnych działających na nią sił zewnętrznych z wyjątkiem grawitacji.

Gdy równowaga elektronów zostanie zakłócona to gęstość elektronów w jakimś obszarze wzrośnie, to będą się one odpychały wzajemnie i dążyły do powrotu do swoich położeń równowagi. Gdy elektrony poruszają się ku swoim pierwotnym położeniom, ich energia kinetyczna rośnie i zamiast zatrzymywać się w położeniach równowagi, biegną one dalej. Będą oscylować tam i z powrotem. W plazmie siłą dążącą do przywrócenia równowagi jest siła elektryczna działająca na elektron.

Chmura elektronów jest odpychana przez siły elektryczne i bezwładność elektronów prowadzi do oscylacji i gęstości. Dlatego też częstość rezonansowa podłużnych fal plazmowych jest równa ω_p: . Zaś w poprzecznych falach elektromagnetycznych okazuje się, że fale poprzeczne są pochłaniane dla częstości niższych niż ω_p.

Plazmon: drgania plazmy, na podłużnym wzbudzeniu gazu elektronowego jako całości. Skwantowane drgania plazmy nazywa się plazmonem.

ZAGADNIENIE 35

FALE ELEKTROMAGNETYCZNE W PLAZMIE, ZALEŻNOŚĆ WSPÓŁCZYNNIKA ODBICIA OD CZĘSTOŚCI, BARWA METALI.

Fala poprzeczna w plazmie , , . Współczynnik odbicia fali od ośrodka może być obliczony ze wzoru: . Przebieg współczynnika odbicia w funkcji częstości przedstawia wykres.

Dla częstości ω­­_p , odbicie jest całkowite. Dla warunku nie obserwujemy w ogóle odbicia promieniowania. Dla tej częstości prąd nośników swobodnych i prąd dielektryczny są równe co do wartości ale przeciwne w fazie. Sumaryczny prąd w ośrodku znika, nie obserwujemy więc efektywnie oddziaływania ośrodka z falą elektromagnetyczną. Dla fala w ośrodku zanika wykładniczo, a więc cała dostarczona energia musi się znaleźć w fali odbitej. Współczynnik odbicia jest więc równy jedności.

ZAGADNIENIE 37

RUCHY JĄDER W KRYSZTAŁACH.

ZAGADNIENIE 38

CIEKŁE KRYSZTAŁY, KSZTAŁT MOLEKUŁ, TYPY CIEKŁYCH KRYSZTAŁÓW, ZASTOSOWANIA.

Ciekłe kryształy - faza mezomorficzna, ciecz anizotropowa; substancja o własnościach pośrednich między własnościami cieczy i kryształu. Są diamagnetykami. Ciekłe kryształy są płynne ze względu na to, że wykazują niższy stopień uporządkowania orientacyjnego cząstek niż ciała stałe. Kształt molekuł - pałeczki lub dyski (ciekłe kryształy kolumnowe)

Zastosowanie:

• fizyka, elektronika, chemia, biologia, farmacja, medycyna, technika materiałowa;

• odczynniki do zegarków elektronicznych, minikalkulatorów, ekranów radarów, paneli ciekłokrystalicznych itp.

Typy ciekłych kryształów:

• Nematyk - istnieje w budowie porządek orientacyjny - cząsteczki są ustawione w przybliżeniu równolegle do pewnego wyróżnionego kierunku opisanego za pomocą wektora jednostkowego.

• Cholesteryk - ten sam sposób uporządkowania co nematyki, lecz wektor jednostkowy nie ma jednak stałego kierunku, lecz rotuje w przestrzeni w sposób okresowy, mają strukturę śrubową.

• Smektyk - w budowie oprócz uporządkowania orientacyjnego panuje również porządek translacyjny (dodatkowe warstwowe ułożenie cząsteczek).

ZAGADNIENIE 39

UKŁADY TERMODYNAMICZNE, ICH RODZAJE, TYPY ŚCIANEK, STAN RÓWNOWAGI TERMODYNAMICZNEJ

Układ termodynamiczny - układ fizyczny podlegający prawom termodynamiki. Układem termodynamicznym jest każde ciało makroskopowe lub zespół takich ciał wzajemnie oddziaływujących na siebie.

Rodzaje układów termodynamicznych.

Układ termodynamiczny otwarty - układ, w którym możliwy jest przepływ materii między nim, otoczeniem.

Układ termodynamiczny zamknięty - układ, którym przepływ materii między nim, a otoczeniem jest niemożliwy.

Układ termodynamiczny jednorodny - układ o jednakowych własnościach fizykochemicznych w każdym punkcie.

Układ termodynamiczny niejednorodny - układ o niejednakowych własnościach fizykochemicznych w każdym punkcie. Układ niejednorodny można zwykle podzielić na jednorodne części.

Układy termodynamiczne dzielimy również na:

Układ izolowany adiabatycznie - układ oddziałujący z otoczeniem jedynie mechanicznie.

Układ izolowany diatermicznie - układ oddziałujący z otoczeniem jedynie termicznie.

Typy ścianek:

Ścianki adiabatyczne - ścianka oddzielająca układ, który oddziałuje z otoczeniem tylko mechanicznie. Przykładem takiej ścianki jest naczynie Dewara.

Ścianki diatermiczne - ścianka oddzielająca układ, który oddziałuje z otoczeniem jedynie termicznie.

Równowaga termodynamiczna - stan układu, w którym nie zachodzą żadne zmiany makroskopowe (przepływy, reakcje chemiczne), a parametry stanu mają wartości stałe, niezależne od czasu.

ZAGADNIENIE 40

PARAMETRY EKSTENSYWNE I INTENSYWNE

Spośród parametrów stanu wyróżnia się parametry intensywne i ekstensywne. Charakteryzują one stan równowagi termodynamicznej układów makroskopowych.

Parametry intensywne.

Parametry ekstensywne.

ZAGADNIENIE 41

I ZASADA TERMODYNAMIKI

Definicja

Zmiana energii wewnętrznej układu termodynamicznego jest równa sumie ciepła pobranego (lub oddanego) przez układ i pracy wykonanej nad układem przez siły zewnętrzne (lub przez układ nad otoczeniem).:

ΔU=ΔQ+ΔW

gdzie :

ΔQ - ilość ciepła

ΔW - praca

ΔQ - przyrost energii wewnętrznej

W przypadku nieskończenie małej zmiany stanu układu, I zasadę zapisujemy w postaci różniczkowej:

dU=dQ+dW

Proces przemiany opisany przez I z. termodynamiki może przebiegać na cztery sposoby:

1. Proces adiabatyczny (dQ=0) - bez wymiany ciepła z otoczeniem

2. Proces izotermiczny (T = const U=const stąd dQ=dW) - temperatura i energia wewnętrzna ciała jest stała

3. Proces izochoryczny (V=const, dW=0) przy stałej objętości.

4. Proces izobaryczny (p=const) przy stałym ciśnieniu.

ZAGADNIENIE 42

II ZASADA TERMODYNAMIKI

Różne sformułowania II zasady:

1. Sformułowanie Plancka - niemożliwe jest zbudowanie maszyny cieplnej działającej cyklicznie, która oziębiałaby zbiornik ciepła i wykonywała pracę nie powodując żadnych zmian w przyrodzie.

2. Sformułowanie Clausiusa - żadna pracująca cyklicznie maszyna nie może bez zmian w otoczeniu przenosić w sposób ciągły ciepła z jednego ciała do drugiego o wyższej temperaturze.

Dla scharakteryzowania procesów termodynamicznych wprowadzimy nową wielkość zwaną entropią S. Jest to termodynamiczna funkcja nie zależna od drogi przejścia od jednego stanu do drugiego, a zależna tylko od początkowego i końcowego stanu układu. A więc entropia jest funkcją stanu określoną dla stanów równowagi i taką że w procesie quasistatycznym:

ZAGADNIENIE 43

RÓWNANIE STANU GAZU DOSKONAŁEGO (RÓWNANIE CLAPEYRONA)

Z własności gazu doskonałego, z założenia, że cząsteczki gazu nie oddziaływają między sobą, poza zderzeniami Wyprowadzono Równanie stanu gazu doskonałego:

p ^. V = n ^. R ^. T

gdzie: n - oznacza liczbę moli danego gazu,

R - jest uniwersalną stałą gazową R=8,314

Stan pewnej stałej ilości gazu określają więc jednoznacznie trzy parametry stanu: ciśnienie p, objętość V i temperatura T.

Z definicji 1 mola gazu i liczby Avogarda N_A=6,023 ^. 10²³ cząsteczek/mol równanie Clapeyrona można zapisać w postaci:

p ^. V = N ^. k ^. T

gdzie: k=R/N_A=1,38 ^. 10²³ J/K - stała Boltzmana

N=N_A - liczba cząstek gazu.

Równanie stanu gazu doskonałego ma w pewnym sensie charakter uniwersalny, nie zawiera bowiem żadnych wielkości charakterystycznych dla gazów i z tego względu równanie możemy stosować dla gazów rzeczywistych.

ZAGADNIENIE 44

GAZY RZECZYWISTE - RÓWNANIE VAN DER WAALSA

Równanie Van der Waalsa opisuje własności gazów rzeczywistych i w odniesieniu do równania Clapeyrona uwzględnia dwie poprawki:

1. Objętość własna cząsteczek gazu - objętość swobodna gazu jest mniejsza od objętości naczynia o objętość własną, którą oznaczamy literą b (dla 1 mola gazu).

2. Siły międzycząsteczkowe - wskutek wzajemnego przyciągania się cząsteczek gazu ciśnienie całkowite jest sumą ciśnienia zewnętrznego i ciśnienia wewnętrznego, które wynosi a/V².

Równanie Van der Waalsa dla 1 mola gazu ma postać:

gdzie: a i b - stałe, charakterystyczne dla danego gazu.

Charakterystyczne cechy izoterm gazu rzeczywistego:

1. W wysokich temperaturach izotermy gazu rzeczywistego są zbliżone do gazu doskonałego.

2. Istnieje pewna temp. -krytyczna poniżej której gaz rzeczywisty może ulec skropleniu, a poniżej której może on występować wyłącznie w stanie gazowym.

3. W temperaturze niższej od krytycznej dana substancja może występować w trzech stanach:

1. jako para nienasycona (w dużych objętościach)

2. jako mieszanina pary nasyconej i cieczy

3. jako ciecz w (małej objętości).

4. W obszarze przejściowym.

5. Punkt krytyczny - przestawia stan, w którym nie ma różnicy między cieczą a gazem. Punkt krytyczny określają: ciśnienie krytyczne p_k, temperatura krytyczna T_k i objętość krytyczna V_k.

ZAGADNIENIE 45

REGUŁA FAZ GIBBSA

Reguła, według której liczba „w” niezależnych parametrów intensywnych, które można zmieniać nie naruszając równowagi „f” faz układu o „s” składnikach, wynosi: w = s - f + n,

gdzie:

n - liczba wszystkich parametrów intensywnych opisujących układ.

Liczbę w nazywa się często liczbą stopni swobody układu wielofazowego. Reguła ta wynika z warunków równowagi termodynamicznej układów wielofazowych. Jeśli w opisie stanu układu wystarczy uwzględnić ciśnienie i temperaturę, to n = 2 i reguła faz Gibbsa przyjmuje postać: w = s -f + 2.

ZAGADNIENIE 46

III ZASADA TERMODYNAMIKI

„W stanach równowagi o zerowej temperaturze termodynamiczna wartość entropii wynosi 0.”

Dla scharakteryzowania procesów termodynamicznych wprowadzimy nową wielkość zwaną entropią S. Jest to termodynamiczna funkcja nie zależna od drogi przejścia od jednego stanu do drugiego, a zależna tylko od początkowego i końcowego stanu układu. A więc entropia jest funkcją stanu określoną dla stanów równowagi i taką że w procesie quasistatycznym:

(1)

(2)

Entropia jest więc funkcją stanu układu i ma tę własność, że w procesach nieodwracalnych zawsze rośnie, a w stanie równowagi układu ma wartość stałą.

Entropie układu można określić metodami fizyki statystycznej gdzie:

(3) S= k ^. lnT

gdzie: k - oznacza stałą Boltzmanna,

T - jest wagą statystyczną stanu makroskopowego i oznacza liczbę stanów mikroskopowych realizujących określony stan makroskopowy.

Wzory (1)(2) określają jedynie przyrost entropii w danym procesie termodynamicznym, nie określają natomiast jej wartości absolutnej w danym stanie układu, podobnie wzór (3), gdyż waga statystyczna stanu T jest określona z jakąś nieznaną dokładnością. Dlatego nie można podać wartości entropii w określonym stanie makroskopowym układu.

Trudności te usunęła zasada sformułowana na podstawie badań właściwości różnych substancji w bardzo niskich temperaturach - III zasada termodynamiki.

III zas. Termodynamiki w sformułowaniu Plancka :

Entropia układu w stanie równowagi zupełnej dąży do zera przy zbliżaniu się do temperatury zera bezwzględnego:

Wyjaśnienia wymaga określenie, ze układ musi być w stanie równowagi zupełnej.

Z energetycznego punktu widzenia chodzi tu o zajęcie przez układ stanu o możliwie najmniejszej energii.

W terminologii chemicznej układ, do którego można stosować III zasadę określa się mianem fazy czystej i skondensowanej;

• przez fazę skondensowaną rozumie się ciało stałe lub ciecz, lecz nie gaz. Entropia gazu nie dąży zatem zera, gdy T0. Ponieważ w odpowiednio niskich temperaturach gaz przechodzi w stan cieczy.

• przez czystość rozumie się takie uporządkowanie atomów lub cząstek, przy którym faza zajmuje stan o najmniejszej energii.

Konsekwencje

Z trzeciej zasady termodynamiki można wywnioskować, że gdy T0 ciepła właściwe i współczynniki rozszerzalności termicznej wszystkich ciał dążą do zera.

Z zasady tej wynika też wniosek o niemożliwości zrealizowania takiego procesu, w wyniku którego ciało ochłodziłoby się do temperatury zera bezwzględnego.

ZAGADNIENIE 47

KINETYCZNA TEORIA GAZÓW, RÓWNANIE PODSTAWOWE, ZASADA EKWIPARTYCJI ENERGII

Równanie podstawowe, opisujące gaz doskonały (równanie Clapeyrona) ma postać:

pV = n_mRT,

gdzie:

n_m - liczba moli, R - uniwersalna stała gazowa (R=8,314 J/mol*K), p - ciśnienie, V - objętość, T - temperatura.

Zasada ekwipartycji.

„Średnia energia kinetyczna gazu dzieli się równomiernie na wszystkie stopnie swobody.”

W modelu jednoatomowym dla cząsteczki średnia energia kinetyczna wynosi: E_K = 3/2kT. Ponieważ cząsteczka jednoatomowa ma 3 stopnie swobody, to na jeden stopień swobody przypada energia równa: 1/2kT. Dla gazu doskonałego, gdy pomijamy oddziaływanie między cząsteczkami, energia wewnętrzna określona jest wzorem U=1/2zRT.

ZAGADNIENIE 48

ROZKŁAD MAXWELLA

Jest to statyczny rozkład prędkości cząsteczek, podlegających prawom fizyki klasycznej, w układzie makroskopowym znajdującym się w równowadze termodynamicznej. Zgodnie z rozkładem Maxwella średnia liczba cząsteczek, których składowe prędkości leżą odpowiednio w przedziałach:

(v _x , v _x + dv _x), (v _y , v _y + dv _y), (v _z , v _z + dv _z),

w jednostce objętości wynosi:

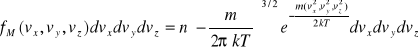
gdzie:

f _M - funkcja Maxwella,

n - gęstość (liczba cząsteczek w jednostce objętości),

m - masa pojedynczej cząsteczki,

k - stała Boltzmanna,

T - temperatura bezwzględna układu.

Rozkład Maxwella opisuje wzór:

.

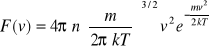
Z rozkładu Maxwella możemy obliczyć trzy najbardziej charakterystyczne prędkości używane w teorii kinetyczno -molekularnej gazów:

Prędkość najbardziej prawdopodobna
.

Prędkość średnia

Prędkość średnia kwadratowa
.

ZAGADNIENIE 49

ROZKŁAD BOLTZMANA, ZJAWISKO TRANSPORTU

Rozkład Boltzmana

Cechą charakterystyczną rozkładu Boltzmana jest to, że jego postać jest niezależna od rodzaju oddziaływań (grawitacyjne, elektryczne, magnetyczne): np., dla cząsteczek naładowanych energia potencjalna będzie różnicą ich elektrostatycznych energii potencjalnych.

Zjawiska transportu - zjawisko transportu ogólnie można scharakteryzować jako przenoszenie pewnej wielkości fizycznej przez ośrodek materialny, przy czym ruchy tego ośrodka mają charakter przypadkowy. Do zjawisk transportu zaliczamy:

1. przepływ prądu elektrycznego (transport ładunku),

2. przewodnictwo cieplne (transport energii),

3. dyfuzję (transport masy),

4. lepkość (transport pędu)

Ad.1 Transport ładunku. Przepływie prądu elektrycznego w metalach polega na uporządkowanym ruchu elektronów swobodnych pod wpływem działania pola elektrycznego. W nieobecności pola pod wpływem temperatury elektrony wykonują chaotyczne ruchy termiczne. Pole elektryczne powoduje dodatkowy ruch, zwany dryfem, który nakłada się na ruch termiczny. Dryf jest uporządkowanym ruchem elektronów w kierunku przeciwnym do kierunku pola elektrycznego.

Równanie transportu ładunku wynika z prawa Ohma:

I = U / R

Korzystając z zależności:

gdzie: q - ładunek,

ρ - opór właściwy

x - długość przewodnika

A - pole przekroju poprzecznego przewodnika

otrzymamy prawo Ohma w postaci :

podstawiając zamiast napięcia U różnicę potencjałów U=V₁-V₂=-ΔV otrzymamy:

Równanie transportu ładunku:

Ad.2 Transport energii - zjawisko przewodnictwa cieplnego polega na przenoszeniu energii cieplnej i jest związane z różnicą temperatur. Jeżeli w warstwie ciała o grubości Δx występuje różnica temperatur ΔT, to wyrażenie ΔT/Δx jest gradientem temperatury. Z doświadczenia wynika, że ilość ciepła dQ/dt przepływającego w jednostce czasu przez jednostkę powierzchni jest proporcjonalne do gradientu temperatury i wyraża się równaniem:

gdzie: A - pole przekroju poprzecznego ciała,

λ - współczynnik przewodnictwa cieplnego, zależny od materiału przewodzącego.

Równanie to jest równaniem transportu energii cieplnej, albo równaniem Fouriera.

Z punktu widzenia mikroskopowego transport energii cieplnej polega w istocie na przekazywaniu energii kinetycznej przez cząstki szybsze (o wyższej temperaturze) cząstkom wolniejszym (chłodniejszym) wskutek przypadkowych zderzeń.

Ad.3. Transport masy - wiadomo, że po otwarciu butelki zawierającej amoniak, eter itp. w krótkim czasie zapach tych cieczy rozchodzi się po całym pomieszczeniu. Jest to najprostszy przykład dyfuzji. Ogólnie dyfuzję można określić jako proces przenoszenia cząstek jakiejś substancji o miejsc o większym stężeniu do miejsc o stężeniu mniejszym, czyli inaczej mówiąc dyfuzja jest transportem masy. Z doświadczenia wynika, że masa ciała przetransportowanego w jednostce czasu dm/dt jest proporcjonalna do gradientu stężenia c tego ciała, tj. do wyrażenia Δc/Δx.

Transport masy jest opisany równaniem Ficka - równaniem transportu masy (równaniem dyfuzji):

gdzie: A - pole przekroju poprzecznego do gradientu stężenia,

D - współczynnik dyfuzji, zależny od rodzaju ciała.

Stężenie c występujące w równaniu oznacza masę dyfundującej substancji przypadającej na jednostkę objętości.

Zjawisko dyfuzji zachodzi najszybciej w gazach, nieco wolniej w cieczach i bardzo powoli w ciałach stałych.

Ad.4. Transport pędu - Znane zjawisko lepkości cieczy polega na tym, że na ciało poruszające się w cieczy działa siła oporu. Rozpatrując najprostszy przypadek, gdy siła dwie płytki znajdujące się w niewielkiej odległości od siebie są zanurzone w cieczy i jedna z nich przesuwa się równolegle względem drugiej. Na płytkę nieruchomą będzie działać wówczas siła lepkości, skierowana zgodnie z kierunkiem ruchu pierwszej płytki. Newton stwierdził, że w tym przypadku siła lepkości F jest proporcjonalna do gradientu prędkości ΔV/Δx, gdzie ΔV oznacza różnicę prędkości płytek, a Δx ich odległość. Prawo Newtona ma postać:

gdzie: η - współczynnik lepkości (zależny od ośrodka)

A - powierzchnia płytek.

Korzystając z II zasady dynamiki siłę F możemy zastąpić pochodną pędu płytki, mamy wówczas Równanie transportu pędu:

Z mikroskopowego punktu widzenia zjawisko lepkości polega na przekazywaniu przez ruchomą płytkę pędu cząsteczką cieczy. Pęd ten jest przenoszony przez cząsteczki cieczy i oddawany w wyniku zderzeń drugiej płytce.

Charakterystyczną cechą transportu pędu jest to, że kierunek przenoszenia wektora pędu jest prostopadły do kierunku wektora pędu, pęd jest więc przenoszony prostopadle do kierunku ruchu cząstek ośrodka.

ZAGADNIENIE 52

POLARYZACJA (ŚWIATŁO SPOLARYZOWANE, RODZAJE POLARYZACJI, SPOSOBY POLARYZOWANIA FAL)

Światło, tak jak promieniowanie elektromagnetyczne jest falą poprzeczną, tzn. kierunki drgań wektorów pól elektrycznego i magnetycznego są prostopadłe do kierunku rozchodzenia się fali. Fale świetlne podlegają również polaryzacji.

Światło spolaryzowane - cechuje uporządkowanie drgań wektora świetlnego.

Wektor świetlny - wektor natężenia pola elektrycznego.

W zależności od tego jakie krzywe regularne zakreśla koniec wektora w czasie, mówimy o:

1. polaryzacji liniowej 2. kołowej 3. eliptycznej

Polaryzacja liniowa - drgania wektora świetlnego odbywają się w jednej płaszczyźnie.

Pol. Kołowa koniec wektora świetlnego ..obserwowany w kierunku rozchodzenia się fali zatacza okrąg.

Polaryzacja eliptyczna - krzywa zakreślana przez koniec wektora jest elipsą.

Metody polaryzacji opierają się na rozłożeniu wiązki na dwa do siebie prostopadłe kierunki drgań i polegają na:

1. podziale wiązki światła nie spolaryzowanego na dwie wiązki spolaryzowane w płaszczyznach prostopadłych.

2. wyeliminowaniu jednej z wiązek.

Sposoby polaryzacji:

1. Poprzez przepuszczenie światła przez płytki polaryzujące (polaroidy) - płytki i liniowo spolaryzowanej powierzchni -przepuszczają jedynie fale równoległe do polaryzacji płytki.

2. polaryzacja przez odbicie - przy pewnym kącie odbicia odbiciu ulegają tylko jedne ze składowych prostopadłych drgań.

3. Polaryzatory dwójłomne - działanie tych polaryzatorów oparte jest na wykorzystaniu zjawiska załamania światła w kryształach anizotropowych (w których wsp. załamania zależy od polaryzacji i kierunku rozchodzenia się fal)

ZAGADNIENIE 53

ODBICIE I ZAŁAMANIE FAL NA GRANICY OŚRODKÓW, WARUNKI BRZEGOWE, WZORY FRESNELA

W przypadku rozwiązywania równań Maxwella w części przestrzeni oprócz warunków początkowych muszą być dane warunki brzegowe w postaci wartości szukanych wielkości na ograniczeniach danego obszaru. W odniesieniu do zagadnień pola elektromagnetycznego nie jest konieczne podawanie wszystkich wektorów wchodzących do równań Maxwella ze względu na związki zachodzące między tymi wektorami. Poprawnie sformułowane warunki graniczne powinny zapewnić jednakowe rozwiązanie problemu, przy czym otrzymane rozwiązanie powinno od tych warunków zależeć w sposób ciągły.

Prawa rządzące odbiciem i załamaniem:

1. Promień odbity i załamany leżą w jednej płaszczyźnie utworzonej przez promień padający i prostopadłą do powierzchni odbijającej w punkcie padania. rys:

• 
  
  
  
  
  
  dla odbicia α = α`

• dla załamania
  

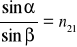
- Stosunek kąta padania do kąta załamania jest równy współczynnikowi załamania ośrodka 2 względem 1 i jest wielkością stałą, zależną jedynie od obu ośrodków i długości fali.

Współczynnik załamania zależy od długości fali.

Warunki na odbicie i załamanie:

• wiązka odbita powstaje tylko wtedy, gdy średnia głębokość nieregularności powierzchni odbijającej jest wyraźnie mniejsza od długości fali światła padającego

• wymiary poprzeczne zwierciadła muszą być znacznie większe od długości fali wiązki padającej.

Wzory Fresnela.

Są to równania opisujące zmiany wektora elektrycznego E fali świetlnej monochromatycznej i liniowo spolaryzowanej na granicy dwóch ośrodków. Wzory te mają postać:

gdzie:

- odpowiednio kąt padania i załamania,

E₁, E₂, E₃ - odpowiednio wartości wektorów promienia padającego, odbitego i załamanego.

Stosunki amplitud E₂ do E₁ nazywa się współczynnikami odbicia Fresnela. Stosunki E₃ do E₁ nazywa się współczynnikami załamania Fresnela. Współczynniki te zależą od długości fali, kierunku padania, stanu polaryzacji światła i własności powierzchni granicznej.

ZAGADNIENIE 54

CAŁKOWITE WEWNĘTRZNE ODBICIE, FALOWODY OPTYCZNE

Falowód - prowadnica falowa - urządzenie (np. w postaci rury metalowej lub pręta dielektrycznego) do przesyłania w przestrzeni fal elektromagnetycznych w określonym kierunku, ograniczające swą powierzchnią boczną ich rozchodzenie się w innych kierunkach. Ograniczenie to jest spowodowane zjawiskiem odbicia od ścian w falowodach metalowych lub zjawiskiem całkowitego wewnętrznego odbicia w falowodach dielektrycznych. Istotną cechą falowodów jest istnienie tylko dyskretnego zbioru rodzajów fal (modów), które mogą się w nim rozchodzić, przy czym każdy mod charakteryzuje się częstotliwością graniczną, powyżej której fala nie jest w falowodzie istotnie tłumiona.

Całkowite wewnętrzne odbicie - jest wówczas, gdy wiązka światła pada z ośrodka o większym współczynniku załamania na ośrodek o mniejszym współczynniku załamania a kąty padania są większe od kąta granicznego. Ogólnie rzecz biorąc nie powstaje załamana wiązka światła. Zjawisku temu towarzyszy zmiana stanu polaryzacji fali świetlnej.

ZAGADNIENIE 55

INTERFERENCJA (POJĘCIE SPÓJNOŚCI ŚWIATŁA, PRZYKŁADY UKŁADÓW, W KTÓRYCH OBSERWUJE SIĘ INTERFERENCJĘ)

Interferencja światła (bo o taką tu chodzi!) jest to zjawisko nakładania się fal świetlnych, w wyniku którego natężenie wypadkowe drgań zależy od różnicy faz drgań składowych. Interferencję światła obserwuje się wówczas, gdy są spełnione następujące warunki:

1. Wiązki światła są przynajmniej częściowo spójne i pochodzą z jednego źródła.

2. Interferujące wiązki mają zbliżone amplitudy, gdyż wtedy właśnie jest możliwe całkowite wygaszanie w minimum.

W wyniku tego zjawiska w poszczególnych miejscach w przestrzeni obserwuje się wzmocnienie lub osłabienie wypadkowej amplitudy drgań świetlnych, a więc i gęstości energii. W wyniku interferencji świetlnej z dwóch różnych źródeł P₁ i P₂ otrzymuje się również drganie sinusoidalne, którego amplituda A zależy od różnicy dróg optycznych r₂ - r₁, przy czym A = 0, gdy r₂ - r₁ = (m+1/2)λ , natomiast A = 2A₀, gdy r₂ - r₁ = mλ , gdzie A₀ - amplitudy interferujących fal, m - liczba całkowita (rząd interferencji).

Spójność światła - koherencja światła - zgodność między fazami w różnych punktach wiązki światła lub w różnych wiązkach. Rozróżnia się spójność czasową i przestrzenną. Spójność czasowa jest to zgodność fazowa między wiązkami promieniowania wychodzącego z jednego punktu źródła rozciągłego po przebyciu przez nie pewnej drogi optycznej. Spójność przestrzenna jest to zgodność fazowa między promieniowaniem dwu różnych punktów źródła rozciągłego w chwili t.

1

l

hω

E

T>0

T=0

f₀

x

0

a

V(x)

ϑ

ΔV_y

Δy

A

V₀

y

F

E

1

x

z

x

E

z

z

x

E

4

3

2

1

0

4

3

2

1

0

n=0

n=1

W

L

L

E

E

dozwolone, puste

dozwolone, wystarczająco wąskie dla przejść termicznych

dozwolone zapełnione

wzbronione

dozwolone zapełnione

dozwolone, puste

wzbronione

dozwolone, częściowo wypełnione

wzbronione

dozwolone zapełnione

3

2

1

2

3

4

c

4

promień padający

α`

α

promień odbity

1

2

promień załamany

β

---