POLITECHNIKA WROCŁAWSKA		Spraw. wyk.: Piotr BARON	Wydział Informatyki i Zarządzania
LABORATORIUM Z FIZYKI Rok: 2 Semestr: 3
Data 14.12.1998	Temat: Pomiar rezystancji.			Ocena:
Nr.lab. : 7. Nr.ćw. : 43.

1. CEL ĆWICZENIA.

Ćwiczenie polegało na pomiarze oporu kilku rezystorów metoda techniczną, a następnie pomierzenie tych samych rezystorów mostkiem Weatstone'a.

2. WSTĘP TEORETYCZNY.

Metoda techniczna: polega na pomiarze napięcia na zaciskach rezystora oraz prądu przepływającego przez ten rezystor. Rezystancje obliczamy ze wzoru R=U/I.

W metodzie tej wykorzystywane są dwa układy pomiarowe:

a)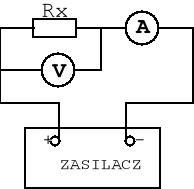
b)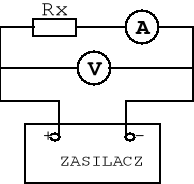

W układzie a woltomierza wskazuje napięcie na Rx, natomiast amperomierz mierzy prąd płynący przez rezystor i woltomierz.

W układzie b amperomierz mierzy prąd płynący przez rezystor Rx, natomiast woltomierz wskazuje napięcie na rezystorze i amperomierzu.

W metodzie technicznej dąży się do maksymalnego uproszczenia obliczeń. Dlatego tez najczęściej pomija się niedokładności związane z rzeczywistymi parametrami mierników (rezystancje amperomierza i woltomierza). Aby jednak tak robić należy stosować się do następującej reguły: Układ a) stosujemy do pomiaru małych rezystancji, a układ b) stosujemy do pomiaru dużych rezystancji. Wynika to z pominięcia małego prądu płynącego przez woltomierz w stosunku do prądu rezystora (w układzie a)) i pominięcia małego spadku napięcia na amperomierzu w stosunku do spadku napięcia na rezystorze (w układzie b)). Wówczas stosujemy zależność:

Metoda mostkowa: polega na doprowadzeniu mostka do stanu równowagi (to taki stan kiedy przez galwanometr - dokładny amperomierz nie płynie prąd.

Układ elektryczny mostka wygląda następująco:

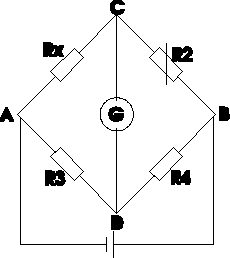
Mostek jest w stanie równowagi gdy G wskazuje 0. Czyli gdy Uac=Uad, a takze Ucb=Udb.

Gdy jest równowaga prąd płynący przez Rx jest równy prądowi płynącemu przez R2, a także prąd płynący przez R3 jest równy prądowi płynącemu przez R4.

Stosując prawo Ohma dla tego układu otrzymujemy: Irx*Rx=Ir3*R3 i Irx*R2=Ir3*R4

z czego:

Rx/R2=R3/R4 stad obliczamy Rx=R3*R2/R4

Dla naszego mostka zestawionego Rx=R2*L1/L2 wynika to z tego, że długość przewodnika L jest wprost proporcjonalna do jego rezystancji.

3. PRZEBIEG ĆWICZENIA

• Orientacyjny pomiar rezystorów omomierzem o małej dokładności

R₁₁=0,43[kΩ] R₁₂=11[kΩ] R₁₃=0,06[kΩ] R₁₄=0,65[kΩ] R₁₅=26[kΩ]

• Pomiary rezystora o dużej rezystancji (R₁₂):

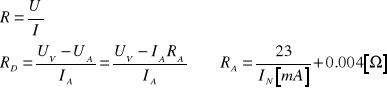
R - rezystancja policzona ze wskazań mierników

Rd - rezystancja dokładna policzona z uwzględnieniem rezystancji amperomierza Ra

Uv - napięcie na woltomierzu

Ua - napięcie na amperomierzu

Ia - prąd płynący przez amperomierz

Ra - rezystancja amperomierza (podana przez producenta tego miernika)

In - zakres pomiarowy amperomierza

R₁₂:

L.p	U [V]	I [mA]	R []	Ra []	Rd []
1	5,3	0,5	10600,00	1,537	10598,463
2	10,3	1	10300,00	1,537	10298,463
3	12,6	1,2	10500,00	1,537	10498,463

Zakres A - 15 mA Zakres V - 15 V

I=15*0.5%=0,075 mA U=15*0.5%=0,075 V Rd=0.82 %

• Pomiary rezystorów o malej rezystancji (R₁₃, R₁₁):

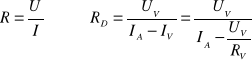
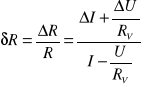
R - rezystancja policzona ze wskazań mierników

Rd - rezystancja dokładna policzona z uwzględnieniem rezystancji woltomierza Rv

Uv - napięcie na woltomierzu

Iv - prąd płynący przez woltomierz

Ia - prąd płynący przez amperomierz

Rv - rezystancja woltomierza (podana przez producenta tego miernika)

R₁₃:

L.p	U [V]	I [mA]	R []	Rv []	Rd []
1	0,85	10	85	7500	85,85
2	1,6	20	80	7500	80,86
3	2,38	30	79,3	7500	80,18

Zakres A - 75 mA Zakres V - 7,5 VI=75*0,5%=0,375 mA U=7,5*0,5%=3,75 V Rd=0.84 %

R₁₁:

L.p	U [V]	I [mA]	R []	Rv []	Rd []
1	4,5	10	450	7500	478,72
2	8,2	20	410	7500	433,70
3	12,2	30	406,6	7500	429,98

Zakres A - 75 mA Zakres V - 7,5 VI=75*0,5%=0,375 mA U=7,5*0,5%=3,75 V Rd=0.84 %

• Pomiary mostkiem Wheatstone'a:

REZYSTOR	R11[]	R12[]	R13[]
L1/L2	1	1	1
R2 []	374.5	10200	74.4
Rx []	374.5	10200	74.4
L1/L2	40/60	40/60	40/60
R2 []	558.1	15500	110.3
Rx []	372.06	10333.33	73.53
L1/L2	60/40	60/40	60/40
R2 []	250.6	6820	50.3
Rx []	375.9	10230	75.45

Rx=R2*L1/L2

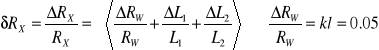
Przyjąłem, że: L1=L2=0.5*0.5=0.25 [cm] Rx=0.05+0.25/50+0.25/50=0.06 %

4. WNIOSKI I DYSKUSJA WYNIKÓW.

Po przeprowadzonych pomiarach okazuje się, ze największa dokładność daje pomiar rezystancji metoda mostkowa (mostkiem fabrycznym). Metoda techniczna dobra jest w przypadku, gdy chcemy zmierzyć opór elementu elektrycznego, a nie zależy nam na zbyt dużej dokładności. Ważne jest tu zastosowanie odpowiedniego układu elektrycznego do przeprowadzenia pomiarów. Chodzi o to, by błąd związany z potraktowaniem mierników jako idealnych (tzn. opór woltomierza równy nieskończoność, a opór amperomierza zero) był do pominięcia. Przy moich pomiarach błędy przy metodzie technicznej osiągnęły wartości 0.84%.

W metodzie technicznej dokładniejszy jest pomiar, gdy uwzględniamy opory amperomierza i woltomierza (wynika to z teoretycznego rozważenia problemu).

Błędy otrzymane przy pomiarze mostkiem Wheatstone'a osiągnęły wartość 0.06% co jest mała wartością w porównaniu z błędami metody technicznej.

Na błędy w metodzie technicznej (oprócz tych związanych z wyborem układu pomiarowego) mogły dodatkowo wpływać: rezystancje przewodów połączeniowych, błędy wynikające z błędnego wskazywania mierników, wzajemny wpływ na siebie prądów płynących w przewodach połączeniowych.

Błąd L otrzymałem poprzez praktyczne ustalenie przesunięcia kontaktu na szynie oporowej takiego, aby wychylenie mikroamperomierza było jeszcze niezauważalne (dokładnie wziąłem połowę tej wartości, bo jest to suma L1+L2).

Mostek Wheatstone'a prawdopodobnie wprowadzał jakiś błąd systematyczny. Sądzę, ze mógł on być spowodowany złym pokazywaniem zera przez mikroamperomierz lub występowaniem jakiejś dodatkowej rezystancji, która dodawała się do rezystancji odpowiadającej L1.

Ponad to błędy w metodzie mostkowej mogły być spowodowane: złym wypoziomowaniem galwanometru, złym jego wyzerowaniem (błąd systematyczny).

- 1 -

---