Równanie fali:

Zachowanie się fali w ośrodku możemy opisać równaniem:

(Fala porusza się w prawo po osi Ox)

Lub (Fala porusza się w lewo po osi Ox)

Dla danego t mamy równanie f(x) opisujące kształt sznura w danej chwili, a dla danego miejsca sznura x mamy równanie f(t) opisujące poprzeczne drgania cząstki sznura w punkcie x.

Rozważać będziemy poprzeczną falę harmoniczną postaci

(13.4)

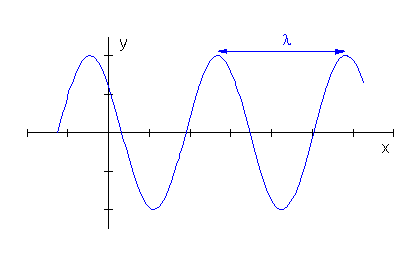
która przedstawia przenoszenie się drgań harmonicznych w kierunku x, i która pokazana jest na rysunku-animacji poniżej (zwykła chamska sinusoida). Stała A (opisująca maksymalne wychylenie)

jest amplitudą
, a wyrażenie
przedstawia fazę
. (Gdy mówimy o wybranej części fali to tym samym mówimy o określonej fazie).

Zauważmy, że wartość wychylenia poprzecznego y  dana wzorem (13.4) jest taka sama w punktach o współrzędnych x, x + λ, x + 2λ, x + 3λ, itd.  Oznacza to, że te punkty mają taką samą fazę.
   Wielkość λ nazywamy długością fali
. Reprezentuje ona odległość między punktami o tej samej fazie na przykład między dwoma grzbietami (maksimami) tak jak na rysunku 13.9.

Czas, w którym fala przebiega odległość równą λ nazywamy okresem T

y_m-to samo co A (wychylenie max)

długość fali λ, okres T, liczba falowa k, częstość kołową ω, częstotliwość f

f=1/T

liczenie „v”-pochodna po czasie, „a” druga pochodna z drogi po czasie

---