rok akademicki 1998/99	L A B O R A T O R I U M Z F I Z Y K I
nr ćwiczenia: 48	Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła matematycznego
wydział: mechaniczny kierunek: mechanika i budowa maszyn grupa: druga	imię i nazwisko: Cezary Jastrzębski
^data wykonania ćw.: 5.11.1998	Ocena		data zaliczenia	podpis
		teoria
		sprawozdanie

1. Cel ćwiczenia:

Wyznaczenie wartości przyspieszenia ziemskiego za pomocą wahadła matematycznego oraz wyznaczenie dekrementu logarytmicznego tłumienia wahadła fizycznego.

2. Wprowadzenie:

Wyznaczanie przyśpieszenia ziemskiego za pomocą wahadła matematycznego.

Aby uniknąć błędu związanego z wyznaczeniem długości wahadła, stosuje się metodę BESSELA polegającą na tym, że wyznacza się okres T₁ wahadła o długości l₁, następnie długość skraca się do l₂ i wyznacza się ponownie okres wahadań a T₂. Wiedząc że: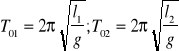
po odpowiednich przekształceniach otrzymamy:
powyższy wzór stanowi podstawę wyznaczania przyśpieszenia ziemskiego w tym ćwiczeniu.

3. Przebieg ćwiczenia.

POMIAR ZREDUKOWANEGO OKRESU WAHAŃ.

Wykonujemy pomiary dla wahadła o długości l₁. Mierzymy czas 100 pełnych wahnięć oraz odczytujemy amplitudy pierwszego i ostatniego wychylenia. Następnie obliczamy okres wahań T₁= t/100

Średni kąt wychylenia oraz zredukowany okres wahań :

sin = (a₁ + a₂)/2l₁;

T₀₁= T₁(1+1/4 sin² 

Wielkości otrzymane bezpośrednio z pomiarów i wyliczone zapisane zostały w tabeli :

dla l₁= 88,0 [cm]

t1	T1	a1	a100	sin	T10
3,14,28	1,90	10	6	5,22	1,90
3,12,00	1,88	10	6,1	5,28	1,88
3,08,59	1,89	10	6	5,22	1,89
3,08,59	1,89	10	5,6	5,11	1,89
3,06,90	1,89	10	5,5	5,05	1,89

dla l1=75,0[cm]

t2	T2	a1	a100	sin	T20
2,53	1,73	10	6,5	6,32	1,73
2,53	1,73	10	6,4	6,28	1,73
2,52	1,72	10	6,3	6,24	1,72
2,54	1,74	10	6,5	6,32	1,74
2,53	1,73	10	6,5	6,32	1,73

WYZNACZANIE LOGARYTMICZNEGO DEKREMENTU

TŁUMIENIA WAHADŁA FIZYCZNEGO

Dla wyznaczenia wartości dekrementu korzysta się ze wzoru:

, gdzie A₁ i A₂ są kolejnymi amplitudami.

Sposób pomiaru:

Wychylamy wahadło z położenia równowagi i mierzymy czas drgań aż do ich całkowitego wygaszenia. Wartości kolejnych amplitud oraz liczbę wahnięć odczytujemy z krzywej zakreślonej przez wahadło. Podobnie obliczamy okres drgań. Wyniki zestawiono w tabeli:

t	n	T	A0	A1	A2	A3	A4	A5	A6	A7	A8	A9
4,47	6	47,84	9,8	8	6,2	4	1,7	0,4

Przykładowe obliczenia i zestawienie wyników :

1) Wahadło matematyczne .

T = t₁/100 sin =

T₁ = 194/100 = 1,94 sin = 5,25

T₁ = 1,92 sin = 5,28

T₁ = 1,88 sin = 5,25

T₁ = 1,88 sin = 5,11

T₁ = 1,86 sin = 5,05

T_1,0 = T1(1+
*sin²/2)

1) T_1,0 = 1,9

2) T_1,0 = 1,88

3) T_1,0 = 1,89

4) T_1,0 = 1,89

5) T_1,0 = 1,89

T_{1,0 śr} = 1,89

T₂ =
sin =
= 0,11 = 6,32

T₂ = 1,73 sin = 6,277

T₂ = 1,73 sin = 6,238

T₂ = 1,72 sin = 6,32

T₂ = 1,74 sin = 6,32

T₂ = 1,73

T_2,0 = T₂ (1+1/4sin²

T_2,0 = 1,73(1+1/4sin²3,16) = 1,73

T_2,0 = 1,73

T_2,0 = 1,72

T_2,0 = 1,74

T_2,0 = 1,73

T_{2,0 śr} = 1,73

g = 39,5

g = 8,9773

g = 8,9773
1,324

g = 9,00 1,32

WAHADŁO FIZYCZNE :

δ = ln

δ₁ = ln
= 0,2029

δ₂ = ln
= 0,2549

δ₃ = ln
= 0,4383

δ₄ = ln
= 0,8557

δ₅ = ln
= 1,4469

δ_śr = 0,64

T =

T =
= 47,84

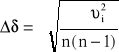
 = δ_śr - δi

δ = 0,2313

δ =   = 0,0134   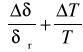

  ,

Uwagi i wnioski

W doświadczeniu I dla jednakowej długości nitki wykonano pięć razy odczyt. Drugi wynik, dla l₁ = 0.75 [m], uznano za błąd gruby, ponieważ to wynika z błędu przyrządu pomiarowego.

Błąd obliczeń wahadła matematycznego był ściśle związany z błędem przyrządu pomiarowego. Nitka wahadła matematycznego była przesunięta o około 0.5 cm od punktu zerowego na skali odczytu amplitudy.

---