GRUPA Czwartek P 15.15-17.50 prowadzący:

Łukasz Tułacz dr Katarzyna Zadarnowska

Karol Sydor

Jacek Kalemba

Zbigniew Duszeńczuk

Podstawy robotyki 2

„Identyfikacja parametrów geometrycznych robota dydaktycznego ROMIK”

1. Cel ćwiczeni.

Celem ćwiczenia jest zapoznanie się ze strukturą kinematyczną robota dydaktycznego ROMIK oraz identyfikacja jego parametrów geometrycznych.

2. Przestrzeń konfiguracyja i zadaniowa.

Przestrzeń konfiguracyjna jest to zbiór wszystkich dopuszczalnych położeń efektora manipulatora opisanych za pomocą jego współrzędnych wewnętrznych (kątów obrotów poszczególnych przegubów), natomiast przestrzeń zadaniowa(robocza) jest opisana za pomocą współrzędnych zewnętrznych(kartezjański układ współrzędnych: x, y, z).

3. Konfiguracja osobliwa i regularna.

Konfiguracje osobliwe to takie wartości współrzędnych wewnętrznych manipulatora, przy których układ zaczyna się zachowywać w inny sposób niż przewidziano. Przykładowo efektor robota może znaleźć się w takim położeniu, w którym pozostanie pomimo ruchów silników. Konfiguracje regularne to zbiór pozostałych konfiguracji(ruch silników powoduje zmianę położenia efektora).

4. Kinematyka prosta i odwrotna.

Kinematyka prosta oparta jest o reprezentację Denavita-Hartenberga której algorytm polega na związaniu z każdym przegubem układu współrzędnych, a następnie określeniu ciągu transformacji sąsiednich i prowadzi do wyliczenia kinematyki manipulatora jako złożenie tych transformacji. Każdą transformację przegubu i−1 do i można opisać jako złożenie elementarnych obrotów i przesunięć:

Paramety
,d,a,
nazywa się parametrami DH

Kinematyka manipulatora określa położenie i orientację efektora względem układu podstawowego I jest opisana złożeniem transformacji:

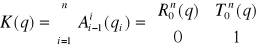
Powyższe odwzorowanie nosi nazwę reprezentacji kinematyki wg DH

Zadanie odwrotne kinematyki (ZOK) - Zadanie polegające na wyznaczeniu ruchów przegubów manipulatora zapewniającego wykonanie określonego ruchu efektora na rozmaitości zadaniowej. Z punktu widzenia sterowania manipulatora zadanie to jest ważniejsze od zadania prostego kinematyki. ZOK może być sformułowane we współrzędnych zadaniowych i przegubowych.

Z punktu widzenia zadanej trajektorii ruchu ZOK dzieli się na:

• Ciągłe ZOK - Mając daną trajektorię ruchu
na rozmaitości zadaniowej, określoną na pewnym przedziale czasu
, wyznaczyć odpowiadającą jej trajektorię ruchu przegubów
, taką że dla
,
.

• Punktowe ZOK - zadanie polegające na osiągnięciu jednego, określonego położenia orientacji efektora
. Rozwiązaniem zadania punktowego jest położenie przegubów
, takie że
.

• Regularne i osobliwe ZOK - ZOK jest regularne, jeśli realizacja trajektorii ruchu efektora nie wymaga wprowadzenia manipulatora w konfiguracje osobliwe. W przeciwnym wypadku ZOK nazywamy osobliwym.

5. Opis mechaniki robota „Romik”

Rozważany manipulator jest manipulatorem klasy 5R(Oznacza to, że manipulator posiada pięć przegubów typu rotacyjnego R), posiadającym pięć stopni swobody. Manipulator ten składa się z pionowej, obrotowej kolumny o wysokości l1, dwuczłonowego ramienia o długości l2 i l3 oraz nadgarstka z efektorem o długości l4, ujmującej długość palców chwytaka. Wszystkie te ogniwa - ramiona są połączone przegubami, których aktualny stan określa wektor stanu
.

6. Przebieg ćwiczenia

6.1. Model kinematyki robota ROMIK

Po dokonaniu obliczeń i serii przekształceń otrzymaliśmy następujący model kinematyki.

Cθ₁ Sθ₄ Cθ₁ Cθ₄ -Sθ₁ | d₃Cθ₁Sθ₄ + d₂Cθ₁Sθ₃ + d₁Cθ₁Sθ₂

A = Sθ₁ Sθ₄ Sθ₁ Cθ₄ -Cθ₁ | d₃Sθ₁Sθ₄ + d₂Sθ₁Sθ₃ + d₁Sθ₁Sθ₂

Cθ₄ -Sθ₄ -1 | d₃Cθ₄ + d₂Cθ₃ + d₁Cθ₂

0 0 0 | 1

A więc macierz translacji będzie wyglądała następująco:

d₃Cθ₁Sθ₄ + d₂Cθ₁Sθ₃ + d₁Cθ₁Sθ₂

T= d₃Sθ₁Sθ₄ + d₂Sθ₁Sθ₃ + d₁Sθ₁Sθ₂

d₃Cθ₄ + d₂Cθ₃ + d₁Cθ₂

1

Znając postać tej macierzy oraz wartości x, y, z możemy obliczyć wartości stałych d_i .

6.2. Obliczenia dla konfiguracji:

θ₁=0°, θ₂=0°, θ₃=90°, θ₄=90° x=285, y=0, z=205

θ₁=0°, θ₂=0°, θ₃=90°, θ₄=45° x=261,57, y=0, z=261,57

Po podstawieniu wartości kątów do macierzy otrzymujemy układ równań:

d₃+ d₂=285

d₁=205

Po rozwiązaniu powyższego układy równań otrzymujemy następujące wartości:

d₁=205, d₂=205, d₃=80.

6.3. Obliczenia dla konfiguracji:

θ₁=0°, θ₂=45°, θ₃=90°, θ₄=90° x=430, y=0, z=145

θ₁=0°, θ₂=90°, θ₃=90°, θ₄=0° x=410, y=0, z=80

Po podstawieniu wartości kątów do macierzy otrzymujemy układ równań:

d₃ = 80

d₁ + d₂ = 410

Po rozwiązaniu powyższego układy równań otrzymujemy następujące wartości:

d₁=205, d₂=205, d₃=80.

7. Wnioski

Widzimy że długości ramion dla poszczególnych konfiguracji wewnętrznych manipulatora wyszły (zgodnie z oczekiwaniami) takie same, jednak należy zauważyć że przy doborze innych kątów pojawiłoby się wiele liczb niewymiernych co znacznie skomplikowałoby obliczenia.

8. Zastosowania manipulatora

Manipulator ma bardzo szeroki zakres zastosowań. Dołączając do niego efektory z róznymi funkcjami możemy otrzymać np. robota spawającego w fabryce samochodów, robota wycinającego różne kształty z jakiegoś materiału, robota wiercącego otwory w płytkach drukowanych, robota mieszającego herbatę, robota zastępującego pałkarza w grze w footbol lub robota do odprowadzania dzieci w przedszkolu za ucho do konta jak coś nabroją.

---