Projekt Z Mechaniki Górotworu

Temat : Ocena Obciążeń działających na obudowę wyrobisk korytarzowych

Prowadzący : dr inż. Andrzej Wojtaszek

Wykonał :

Mariusz Stasiak

Rok IV

Specjalność GIF

SPIS TREŚCI:

1. Wprowadzenie.

1. Temat projektu.

2. Cel i zakres opracowania.

2. Warunki geotechniczno - górnicze.

1. W nadkładzie.

1. Opis geologiczny nadkładu.

2. Ustalenie średnich parametrów nadkładu do określenia pierwotnego stanu naprężeń w miejscu posadowienia wyrobiska.

2. Wokół wyrobiska.

1. Zestawienie parametrów geotechnicznych skał wokół projektowanego chodnika.

2. Ocena parametrów geotechnicznych masywu skalnego otaczającego wyrobisko korytarzowe.

3. Określenie obliczeniowych parametrów geotechnicznych masywu uśrednionego wokół chodnika.

3. Określenie obciążeń działających na obudowę wyrobiska korytarzowego.

1. Stan naprężeń wokół wyrobiska korytarzowego.

1. Określenie pierwotnego stanu naprężeń w miejscu lokalizacji chodnika, analiza stanu wytężenia masywu przed wykonaniem wyrobiska.

2. Prognoza możliwości lokalnej utraty stateczności po wykonaniu wyrobiska.

2. Metody określania ciśnienia statycznego górotworu - analiza skutków lokalnej utraty stateczności.

1. Metody Protodiakonowa lub Cymbarewicza.

2. Teoria sklepienia ciśnień wg Sałustowicza lub zmodyfikowana hipoteza Sałustowicza

3. Wybór metody obliczeń i jego uzasadnienie.

3. Analiza oddziaływań górotworu na obudowę wyrobiska korytarzowego posadowionego poniżej głębokości krytycznej

1. Prognoza globalnej utraty stateczności

2. Model górotworu otaczającego wyrobisko poniżej głębokości krytycznej.

3. Ustalenie modelu obliczeniowego, założenia do obliczeń metodami analitycznymi.

4. Rozkład naprężeń wtórnych wokół modelu wyrobiska posadowionego poniżej głębokości krytycznej.

5. Oddziaływanie górotworu na obudowę wyrobiska.

4. Stan przemieszczeń wokół wyrobiska - zaciskanie wyrobiska.

1. Model obliczeniowy i wyjaśnienie założeń do obliczeń.

5. Charakterystyka obciążeniowa górotworu

1. Wyznaczenie charakterystyki obciążeniowej górotworu i jej ilustracja graficzna.

2. Ustalenie optymalnych warunków obciążenia i zaciskania obudowy.

3. Analiza wpływu parametrów górotworu na przebieg charakterystyki obciążeniowej.

6. Ustalenie obciążeń działających na obudowę projektowanego wyrobiska korytarzowego

1. Analiza wyników przeprowadzonych obliczeń.

2. Zestawienie obciążeń działających na obudowę w stropie i w ociosach wyrobiska.

4. Wytyczne dla służb geotechnicznych.

5. Literatura.

1.

WPROWADZENIE

1.1

TEMAT PROJEKTU

Tematem tego projektu jest ocena obciążeń działających na obudowę wyrobisk korytarzowych.

1.2

Cel i zakres opracowania

Cel opracowania:

• wyznaczenie obciążeń działających na wyrobisko korytarzowe,

• sporządzenie charakterystyki obciążeniowej górotworu,

• przeanalizowanie wpływu R_cg na wielkość obciążeń obudowy i jej zaciskanie.

Zakres opracowania:

• warunki geotechniczno - górnicze;

• określenie obciążeń działających na obudowę wyrobiska korytarzowego:

• stan naprężeń wokół wyrobiska korytarzowego;

• metody określania ciśnienia statycznego górotworu - analiza skutków lokalnej utraty stateczności;

• analiza oddziaływań górotworu na obudowę wyrobiska korytarzowego posadowionego poniżej głębokości krytycznej;

• stan przemieszczeń wokół - zaciskanie wyrobiska;

• charakterystyka obciążeniowa górotworu;

• ustalenie obciążeń działających na obudowę projektowanego wyrobiska korytarzowego;

• wytyczne dla służb geotechnicznych;

• literatura;

2.

WARUNKI GEOTECHNICZNO - GÓRNICZE

2.1

W NADKŁADZIE

2.1.1

OPIS GEOLOGICZNY NADKŁADU

Złoże rud miedzi obszaru górniczego Rudna położone jest w środkowej części Monokliny Przedsudeckiej. Od południa monoklinę tą ogranicza blok przedsudecki, który składa się ze skał magmowych i metamorficznych pochodzących z proterozoiku i starego paleozoiku. Skały te budują również podłoże monokliny. Zarówno monoklina jak i blok przed sudecki wchodzą w skład większej jednostki - strefy przedsudeckiej.

Budowa geologiczna obszaru górniczego Rudna składa się z dwóch kompleksów skał.

Starszy kompleks obejmuje okresy perm i trias: należą tu czerwony spągowiec, w skład którego wchodzą piaskowce czerwone w stropie szare, cechsztyn czyli łupki miedzionośne, dolomity, wapienie i anhydryty, pstry piaskowiec składający się z piaskowców czerwonych i szarych.

Kompleks młodszy, kenozoiczny obejmuje: trzeciorzęd na który składają się piaski, żwiry, mułówce mułowce i węgiel brunatny, oraz czwartorzęd zbudowany z pisków i glin.

Złoża rud miedzi zalegają na głębokości od 850 m przy południowo-zachodniej granicy obszaru górniczego. Wewnętrzna budowa złoża jest zróżnicowana. Okruszcowaniem objęte są trzy odmiany litologiczne skał. W profilu pionowym można wyróżnić: rudę piaskową, rudę łupkową, rudę wapienno-dolomitową.

Te odmiany rud charakteryzują się dużą zmiennością miąższości, niekiedy nawet obserwowany jest zanik okruszcowania w poszczególnych odmianach litologicznych. Złoże bilansowane nie posiada nie posiada naturalnych powierzchni wyznaczających jego strop i spąg, zajego granice uważa się powierzchnie wyznaczone na podstawie próbkowania wyrobisk górniczych.

Średnią miąższość złoża bilansowego w obszarze udokumentowanym ZG Rudna wynosi 5,7 m. Osady permu i triasu, z których zbudowana jest monoklina, w rejonie obszaru górniczego Rudna mają rozciągłość NW-SE WSE zapadają pod kątem 3-6° na północny-wschód.

2.1.2

Ustalenie średnich parametrów nadkładu do określenia pierwotnego stanu naprężeń w miejscu posadowienia wyrobiska

tABELA 1. ŚREDNIE PARAMETRY NADKŁADU

Lp.	Nazwa skały	Głębokość zalegania [m]	Miąższość warstwy [m]	Ciężar objętościowy [MN/m^3]
1	Nadkład	-	827,4	0,022
2	Anhydryt przeławicony dolomitem	850,0	22,6	0,026
3	Dolomit zbity, w spągu okruszcowany chalkozynem i chalkopirytem	856,0	6,0	0,023
4	Łupek dolomityczny ilasty	856,3	0,3	0,023
5	Wapień dolomityczny	859,8	3,5	0,025
6	Piaskowiec ilasty okruszcowany	862,0	2,2	0,025
7	Piaskowiec drobnoziarnisty, szary	867,0	5,0	0,025

2.2

WOKÓŁ WYROBISKA

2.2.1

USTALENIE ŚREDNICH PARAMETRÓW NADKŁADU DO OKREŚLENIA PIERWOTNEGO STANU NAPRĘŻEŃ W MIEJSCU POSADOWIENIA CHODNIKA

Tabela 2. normowe parametry geotechniczne skał

Nazwa skały	Miąższość [m]	Jakość górotworu		Normowe parametry geotechniczne skał
				Rozmakalność	Podzielność	[MP]	[MP]	[GPa]		[°]
Anhydryt przeławicony dolomitem	22,6	1,0	PŁ	92,7	6,3	38,6	0,17	40,0
Dolomit zbity, w spągu okruszcowany chalkozynem i chalkopirytem	6,0	1,0	PŁ	94,9	7,5	49,2	0,23	40,0
Łupek dolomityczny ilasty	0,3	0,8	K	26,0	1,6	11,7	0,16	30,0
Wapień dolomityczny	3,5	0,9	PŁ	69,3	5,5	39,3	0,22	36,0
Piaskowiec ilasty okruszcowany	2,2	0,6	PŁ	42,8	2,0	14,5	0,18	30,3
Piaskowiec drobnoziarnisty, szary	5,0	0,8	B	24,7	1,08	13,1	0,19	37,6

Parametry obliczeniowe skał wyznacza się mnożąc wartości parametrów normowych przez współczynnik k, różny dla każdego parametru.

Parametr	Rc	Rr	Es	ν	φs
k	0,7	0,6	0,7	0,9	0,9

Tablica 3. obliczeniowe parametry geotechniczne skał

Nazwa skały	Miąższość [m]	Jakość górotworu		Obliczeniowe parametry geotechniczne skał
				Rozmakalność	Podzielność	[MP]	[MP]	[GPa]		[°]
Anhydryt przeławicony dolomitem	22,6	1,0	PŁ	64,89	3,75	27,02	0,15	36,0
Dolomit zbity, w spągu okruszcowany chalkozynem i chalkopirytem	6,0	1,0	PŁ	66,43	4,50	34,44	0,21	36,0
Łupek dolomityczny ilasty	0,3	0,8	K	18,20	0,96	8,19	0,14	27,0
Wapień dolomityczny	3,5	0,9	PŁ	48,51	3,30	27,51	0,20	32,40
Piaskowiec ilasty okruszcowany	2,2	0,6	PŁ	29,96	1,20	10,15	0,16	27,00
Piaskowiec drobnoziarnisty, szary	5,0	0,8	B	17,29	0,65	9,17	0,17	33,84

Określenie wartości parametrów geotechnicznych masywu skalnego otaczającego wyrobisko korytarzowe

Parametry geotechniczne górotworu dobrane zostały z normy PN-G-05020

• Wytrzymałość górotworu na ściskanie
  

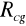
• Kąt tarcia wewnętrznego górotworu
  

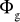
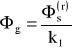
• Współczynnik sprężystości górotworu
  

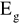
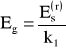
• Współczynnik Poissona
  

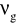
Tablica 4. PARAMETRY GEOTECHNICZNE GÓROTWORU

Nazwa skały	Podzielność	k0	k1	Rcg [MPa]	Eg [GPa]	νg	Φg [°]
Anhydryt przeławicony dolomitem	PŁ	0,7	1,05	45,42	25,73	0,14	34,29
Dolomit zbity, w spągu okruszcowany chalkozynem i chalkopirytem	PŁ	0,7	1,05	46,50	32,80	0,20	34,29
Łupek dolomityczny ilasty	K	0,5	1,20	9,10	6,83	0,12	22,50
Wapień dolomityczny	PŁ	0,7	1,05	33,96	26,20	0,19	30,86
Piaskowiec ilasty okruszcowany	PŁ	0,5	1,10	14,98	9,23	0,15	24,55
Piaskowiec drobnoziarnisty, szary	B	0,5	1,15	8,65	7,97	0,15	29,43

Określenie OBLICZENIOWYCH PARAMETRÓW GEOTECHNICZNYCH masywu uśrednionego wokół chodnika

W przypadku występowania różnych rodzajów skał wokół wyrobiska, parametry geotechniczne wyznacza się jako średnie ważone wg wzoru

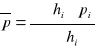
gdzie :

p_i - parametr i-tej warstwy

h_i - miąższość warstwy

Określając średnią ważoną bierze się pod uwagę obszar o zasięgu w pionie nie mniejszy niż 2,5 h ( wysokości wyrobiska), o podziale takim, że w projekcie obszar nad stropem wynosi

7,0 [m], zaś obszar pod spągiem 3,5 [m].

Przykład obliczeń dla R_cg :

=

Tablica 5. PARAMETRY GEOTECHNICZNE MASYWU UŚREDNIONEGO

[MPa]	[°]	[GPa	-	[MPa
31,96	31,20	22,30	0,17	5,0

3.

OKREŚLENIE OBCĄŻEŃ DZIAŁAJĄCYCH NA OBUDOWĘ WYROBISKA KORYTARZOWEGO

3.1

STAN NAPRĘŻEŃ WOKÓŁ WYROBISKA KORYTARZOWEGO

3.1.1

OKREŚLENIE PIERWOTNEGO STANU NAPRĘŻEŃ W MIEJSCU LOKALIZACJI CHODNIKA, ANALIZA STANU WYTĘŻENIA MASYWU PRZED WYKONANIEM WYROBISKA

W miejscu posadowienia chodnika na skały działają dwa rodzaje naprężeń :

- ciśnienie pionowe, będące bezpośrednio wynikiem ciężaru nadkładu

- ciśnienie boczne, spowodowane pośrednio ciężarem nadkładu, ponieważ każda cząstka skały obciążona nadkładem stara się zwiększyć swe wymiary poprzeczne, co jest uniemożliwiane przez sąsiadujące z nią cząstki.

- ciśnienie pionowe P_z

P_z =

gdzie:

γ_i - ciężar objętościowy i-tej warstwy [kN/m³],

h_i - miąższość i-tej warstwy [m],

- ciśnienie boczne P_x

P_x = P_z ·

Przykładowe obliczenia dla warstwy wapienia dolomitycznego:

P_z = 0,022·827,4 + 0,026·22,6 + 0,023·6,0 + 0,023·0,3 + 0,025·3,5 = 19,023 [MPa]

P_xstropu = 18,935·0,2987 = 5,656 [MPa]

P_xspągu = 19,023·0,2987 = 5,682 [MPa]

Tablica 6. PIERWOTNY STAN NAPRĘŻEŃ W MIEJSCU LOKALIZACJI CHODNIKA

Nazwa skały	Głębokość Zalegania [m]	Miąższość [m]	γ [MN/m^3]	ν -	Pz [MPa]	Px [MPa]		Rcg [MPa]
													strop	spąg
Nadkład	827,4	827,4	0,022	-	18,203	-	-
Anhydryt przeławicony dolomitem	850,0	22,6	0,026	0,17	18,970	3,728	3,849	45,42
Dolomit zbity, w spągu okruszcowany chalkozynem i chalkopirytem	856,0	6,0	0,023	0,16	18,928	3,579	3,605	46,50
Łupek dolomityczny ilasty	856,3	0,3	0,023	0,20	18,935	4,732	4,734	9,10
Wapień dolomityczny	859,8	3,5	0,025	0,23	19,023	5,656	8,682	33,96
Piaskowiec ilasty okruszcowany	862,0	2,2	0,025	0,23	19,078	5,682	5,699	14,98
Piaskowiec drobnoziarnisty, szary	867,0	5,0	0,025	0,19	19,203	4,475	4,504	8,65

Analiza stanu wytężenia masywu przed wykonaniem wyrobiska

Z powyższego zestawienia wynikają następujące wnioski :

· Strop wyrobiska, który stanowi dolomit znajduje się w stanie sprężystym ( P_z > R_cg ) i jest w stanie przenieść obciążenie nadkładu na ociosy, gdyż nie została przekroczona wytrzymałość na ściskanie R_cg = 46,5 MPa przez ciśnienie pionowe pierwotne P_z = 18,928 MPa

· Ociosy wyrobiska tworzone przez łupek dolomityczny, wapień dolomityczny oraz piaskowiec ilasty ulegną zniszczeniu pod wpływem obciążenia, jakie przeniesie na nie warstwa stropowa, gdyż ich wytrzymałość na ściskanie jest mniejsza od pierwotnego ciśnienia pionowego ( wyjątek stanowi środkowa warstwa ociosu - wapień dolomityczny, którego wytrzymałość na ściskanie jest większa od pierwotnego ciśnienia pionowego

R_cg = 33,96 MPa > P_z = 19,023 MPa)

·Spąg zbudowany przez piaskowiec drobnoziarnisty ma najniższą wytrzymałość na ściskanie równą 8,65 MPa i będzie ulegał niszczeniu w postaci wypiętrzeń spągu. Ciśnienie pionowe pierwotne P_z = 19,078 MPa_l tej warstwy przekracza wartość wytrzymałości na ściskanie.

PROGNOZA MOŻLIWOŚCI UTRATY LOKALNEJ STATECZNOŚCI PO WYKONANIU WYROBISKA

Określenie wtórnego stanu naprężeń polega na obliczeniu naprężeń pionowych w stropie wyrobiska chodnikowego oraz naprężeń poziomych w ociosach tegoż wyrobiska i sprawdzeniu czy strop i ociosy nie ulegną zniszczeniu. To z kolei pozwala na dobranie odpowiedniej hipotezy określenia ciśnienia statycznego górotworu.

Naprężenia poziome σ_x

σ_x = σ_xmax = p_x(1+β) - p_z

σ_x = 0

Naprężenia pionowe σ_z

σ_z = 0

σ_z = σ_zmax = p_z(1+α) - p_x

α, β oznaczają współczynniki kształtu zależne od stosunku szerokości chodnika b do jego wysokości h.

b/h	50,00	20,00	5,00	1,00	0,20	0,05	0,02
	17,00	4,00	2,00	0,84	0,20	0,02	0,01
	0,01	0,02	0,20	0,84	2,00	4,00	17,00

W przypadku danych z projektu
= 1,143 zaś współczynniki α i β zostały wyliczone przez interpolację z powyższej tabeli:

Określenie σ_x w stropie

- w warstwie dolomitu zbitego

σ_x = 3,605 ( 1+ 0,81712 ) - 18,928 = - 12,377 MPa

σ_z = 0

Określenie σ_z w ociosie

- w warstwie łupka ilastego

σ_z = 18,935 ( 1+ 0,88147 ) - 4,734 = 30,892 MPa

σ_x = 0

- w warstwie wapienia dolomitycznego

σ_z = 19,023 ( 1+ 0,88147 ) - 5,682 = 30,109 MPa

σ_x = 0

- w warstwie piaskowca ilastego okruszcowanego

σ_z = 19,078 ( 1+ 0,88147 ) - 5,699 = 30,196 MPa

σ_x = 0

Analiza stanu wytężenia masywu w otoczeniu wykonanego wyrobiska

W analizie należy porównać wartości naprężenia σ_x z wartościami wytrzymałości na rozciąganie R_r oraz wartości σ_z z wytrzymałością na ściskanie R_cg .

Jeśli spełniony zostanie warunek

dla wszystkich warstw, to zniszczeniu ulegnie tylko strop.

Jeżeli w zostanie spełniony warunek

dla chociaż jednej warstwy , to zniszczeniu ulegnie i strop i spąg.

Porównanie

• Naprężeń poziomych
  

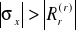
- dolomit zbity

σ_x = - 12,377 Mpa R_r = 4,5 MPa

• Naprężeń pionowych
  

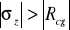
- łupek dolomityczny

α_z = 30,892 MPa R_cg = 9,10 MPa

- wapień dolomityczny

α_z = 30,109 MPa R_cg = 33,96 MPa

- piaskowiec ilasty

α_z = 30,196 MPa R_cg = 14,98 MPa

Powyższa analiza wykazuje , że zniszczeniu ulegną zarówno ociosy jak i strop. Analiza skutków utraty lokalnej stateczności zostanie przeprowadzona metodą przewidującą zniszczenie ociosów - hipoteza Cymbarewicza lub zmodyfikowana hipoteza Sałustowicza.

3.2

METODY OKREŚLANIA CIŚNIENIA STATYCZNEGO GÓROTWORU - ANALIZA SKUTKÓW LOKALNEJ UTRATY STATECZNOŚCI

3.2.1

METODY PRODODIAKONOWA LUB CYMBAREWICZA

Po wykonaniu wyrobiska następuje deformacja górotworu. Zjawiskiem pierwotnym wywołanym taką deformacją jest ciśnienie deformacyjne, inaczej dynamiczne. Zjawiskiem wtórnym - spękanie skał w stropie, często także w ociosach i spągu. Spękania takie występują, gdy przekroczone zostają wytrzymałości na rozciąganie i ścinanie w naprężeniach stropu i spągu, a w ociosach na ciśnienie. W obszarach tych powstają strefy odprężone, które oddzielając się od calizny, obciążają swoim ciężarem obudowę. Obciążenie to ma charakter ciśnienia statycznego.

Według teorii Protodiakonowa nad wyrobiskiem w warstwie stropowej wytwarza się sklepienie rozkładające ciężar nadkładu na ociosy, a na obudowę działa jedynie ciężar części warstwy położonej wewnątrz sklepienia.

Uzupełnieniem teorii Protodiakonowa jest teoria Cymbarewicza, zakłądająca, że oprócz strefy odprężonej w stropie powstaje strefa odprężona wzdłuż ociosów wyrobiska, a spękane skały swym ciężarem obciążają obudowę zarówno w kierunku pionowym jak i poziomym.

W danym wyrobisku oprócz strefy odprężonej w stropie powstaje strefa odprężona wzdłuż ociosów, dalsze obliczenia więc będą prowadzone według teorii Cymbarewicza.

• dla ociosów

= arctg
,

gdzie :

- pozorny kąt tarcia wewnętrznego skał

R_cs - wytrzymałość skał na ściskanie,
- średnia ważona

= arctg
= arctg 3,222 = 72,76

=
,

gdzie :

- pozorny kąt tarcia wewnętrznego górotworu

k₁ - wskaźnik podzielności i rozmakalności skał

=
= 66,14

• dla stropu

= arctg
= arctg 6,643 = 81,43

=
= 77,55

Zasięg strefy spękań h_o oblicza się ze wzoru:

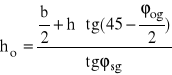
h_o = 1,21 m

Określenie obciążeń obudowy wyrobiska:

• obciążenie pionowe:

• obciążenia poziome na krańcach ociosów:

3.3.2

TEORIA SKLEPIENIA CIŚNIEŃ WG SAŁUSTOWICZA LUB ZMODYFIKOWANA HIPOTEZA SAŁUSTOWICZA

Sałustowicz w swej teorii sklepienia ciśnień wyszedł z założenia, że strefa spękań wokół wyrobiska wynika z naturalnej skłonności skał do przystosowania wyłomu do takiego kształtu, przy którym maksymalne naprężenia zrównują się z wytrzymałością na rozciąganie.

Takim optymalnym kształtem jest przekrój eliptyczny.

Zmodyfikowana teoria Sałustowicza jest połączeniem teorii sklepienia ciśnień

A. Sałustowicza i teorii P.M. Cymbarewicza, w której oś pozioma elipsy sklepienia ciśnień jest powiększona w stosunku do szerokości chodnika o dwa odcinki, które wyznacza kąt płaszczyzn poślizgu w ociosach, w połowie wysokości wyrobiska.

h_o = a₁ -

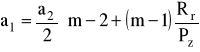
=2,96

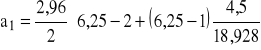
= 8,14

h_o = 8,14 - 3,5 = 4,64

3.2.3

WYBÓR METODY OBLICZEŃ I JEJ UZASADNIENIE

Zestawienie wyników

Rodzaj metody	ho	qz
Metoda Cymbarewicza	1,21	0,027
Zmodyfikowana metoda Sałustowicza	4,64	0,10

Według słów Z. Kłeczka w praktyce najbardziej adekwatne do rzeczywistości wyniki daje metoda Cymbarewicza, według której obciążenie przypadające na ociosy wyrobiska stanowi różnicę pomiędzy całkowitym ciężarem skał zawartych wewnątrz strefy spękań, a ciężarem skał obciążających strop wyrobiska. Zgodnie z tymi słowami przyjmuję metodę Cymbarewicza.

3.3

ANALIZA ODDZIAŁYWAŃ GÓROTWORU NA OBUDOWĘ WYROBISKA KORYTARZOWEGO POSADOWIONEGO PONIŻEJ GŁĘBOKOŚCI KRYTYCZNEJ

3.3.1

PROGNOZA GLOBALNEJ UTRATY STATECZNOŚCI

Globalna utrata stateczności ma miejsce wtedy, gdy wyrobisko znajduje się poniżej głębokości krytycznej (H > H_kr), następuje wówczas przekroczenie ciśnienia użytecznego. Koncentracja naprężeń ściskających jest tak duża, że przekraczają one wytrzymałość na ściskanie. Taka też sytuacja ma miejsce w przypadku rozpatrywanego wyrobiska.

H_kr =
=
= 720,23 m

Wyrobisko posadowione jest na głębokości H = 862,0 m. Głębokość krytyczna została zatem przekroczona.

3.3.2

MODEL GÓROTWORU OTACZAJĄCEGO WYROBISKO PONIŻEJ GŁĘBOKOŚCI KRYTYCZNEJ

Wyrobisko posadowione jest poniżej głębokości krytycznej (H>H_kr), więc w dalszych obliczeniach i rozważaniach przyjmujemy model sprężysto - plastyczny górotworu. Skutekiem lokalnej koncentracji naprężeń w obszarze górotworu otaczającego wyrobisko, następuje przejście ze stanu sprężystego w stan plastyczny.

3.3.3

USTALENIE MODELU OBLICZENIOWEGO, ZAŁOŻENIA DO OBLICZEŃ METODAMI ANALITYCZNYMI

Założenia :

• ośrodek jest ciągły i jednorodny

• ośrodek jest nieściśliwy w strefie plastycznej

• ośrodek jest ciągły

• naprężenia radialne są ciągłe

gdzie :

I - górotwór nienaruszony,

II - górotwór naruszony,

c - spójność górotworu przed zniszczeniem,

c^' - spójność górotworu po zniszczeniu,

3.3.4

ROZKŁAD NAPRĘŻEŃ WTÓRNYCH WOKÓŁ MODELU WYROBISKA POSADOWIONEGO PONIŻEJ GŁĘBOKOŚCI KRYTYCZNEJ

gdzie :

P_a - oddziaływanie deformacyjne

P_g - oddziaływanie radialne strefy sprężystej

P_z - pierwotny stan naprężeń pionowych,

q - oddziaływanie statyczne w stropie wyrobiska,

W takim układzie masyw oddziałuje na obudowę jako :

- oddziaływanie deformacyjne P_a jako resztkowe ciśnienie pierwotne wynikające z oddziaływania strefy sprężystej - czyli odpowiednio zredukowane ciśnienie P_z

- oddziaływanie statyczne q jako bezpośrednie ciśnienie spowodowane ciężarem strefy

odprężonej - czyli rozłożony ciężar strefy plastycznej.

Rozkład naprężeń w strefie plastycznej

r > r_L

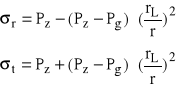
granica: r = r_L

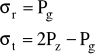
Rozkład naprężeń w strefie sprężystej

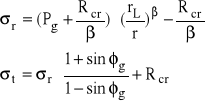
granica: r = r_L

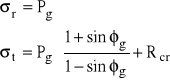
gdzie:

P_g - oddziaływanie radialne strefy sprężystej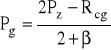

P_z - pierwotny stan naprężeń pionowych

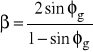
- parametr występujący w równaniach

1,436 MPa

Krawędź wyrobiska

(r = r_w)

- funkcja zasięgu strefy plastycznej

Założenie: P_a=0

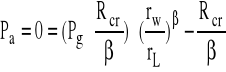
r_L = r_Lg - graniczny zasięg strefy plastycznej;

r_w - zastępczy promień wyrobiska

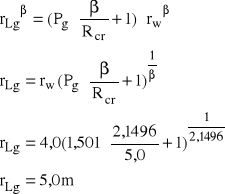
Dane potrzebne do wykresu :

R_cg = 31,96 MPa

R_cr = 5,0 Mpa

P_z = 18,96 MPa

P_g = 1,436 MPa

r_lg = 5,0 m

Rys. 6. Naprężenia w strefach obliczeniowych wokół wyrobiska

3.3.5

ODDZIAŁYWANIE GÓROTWORU NA OBUDOWĘ WYROBISKA

Powstanie ciśnienia deformacyjnego które działa na obudowę wyrobiska górniczego daje możliwość przemieszczania się konturów wyrobiska ku środkowi przekroju i jednoczesnemu przeciwstawianiu się tym przemieszczeniom przez założoną w wyrobisku obudowę. Przylegająca w miarę ściśle do ociosów i stropu wyrobiska obudowa stanowi przeszkodę dla przemieszczeń musi więc tym samym doznawać pewnych obciążeń, przy czym wartość tych obciążeń uzależniona jest niewątpliwie od wielkości przemieszczeń.

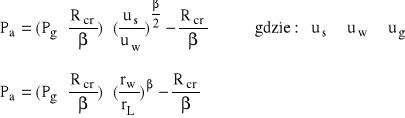
Rys. 7. Oddziaływanie deformacyjne

Oddziaływanie statyczne górotworu w stropie wyrobiska q=f(r_L)

Ciśnienie to występuje w postaci ciśnień pionowych, określa się go jako całkowity ciężar górotworu naruszonego.

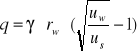
gdzie:

u_w - wymuszone przemieszczenie konturu wyrobiska,

u_g - przemieszczenie graniczne,

u_s - przemieszczenie sprężyste,

P_­g - oddziaływanie radialne strefy sprężystej,

Rys. 8. Oddziaływanie statyczne w stropie wyrobiska.

3.4

STAN PRZEMIESZCZEŃ WOKÓŁ WYROBISKA - ZACISKANIE WYROBISKA

3.4.1

MODEL OBLICZENIOWY I WYJAŚNIENIE ZAŁOŻEŃ DO OBLICZEŃ

Założenia:

- nieściśliwość strefy plastycznej,

- odkształca się tylko strefa sprężysta,

- przyjmujemy, że
, z tego wymuszone przemieszczenie konturu wyrobiska u_w wynosi

• odkształcenie względne w strefie sprężystej:

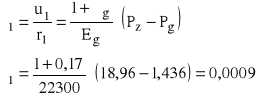
• przemieszczenie sprężyste

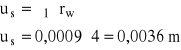
• przemieszczenia graniczne

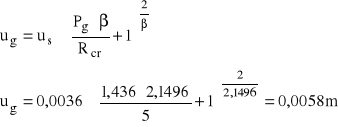
• oddziaływanie statyczne

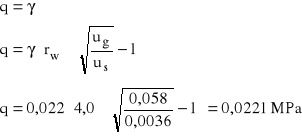
3.5

CHARAKTERYSTYKA OBCIĄŻENIOWA GÓROTWORU

3.5.1

WYZNACZENIE CHARAKTERYSTYKI OBCIĄŻENIOWEJ GÓROTWORU I JEJ ILUSTRACJA GRAFICZNA.

Polska Norma określa minimalny nacisk na obudowę i odpowiadające mu optymalne przemieszczenie konturu wyrobiska u_opt z przecięcia się dwóch krzywych P_a i q.

gdzie:

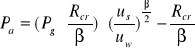
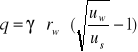
Porównując powyższe równania otrzymamy u_opt = u_w

Rys. 10. Wykres zależności P_v = f(u_w)

Dane :

us [m]	ug [m]	Pg [MPa]	Rcr [MPa]	β	[MN/m^3]	rw [m]
0,0037	0,0058	1,436	5,0	2,1496	0,022	4,0

u_s ≤ u_w ≤u_g

0,0037 ≤ u_w ≤ 0,0058

uw [m]	q [kPa]	Pa [kPa]	Pv [kPa]
0,003678	0	1436,28	1436,28
0,003818	1,663416	1287,811	1289,475
0,003956	3,269123	1152,496	1155,766
0,004094	4,84706	1026,633	1031,48
0,004232	6,398618	909,2747	915,6733
0,004370	7,925079	799,5964	807,5215
0,004508	9,427623	696,8762	706,3038
0,004646	10,90734	600,4793	611,3866
0,004784	12,36524	509,8454	522,2106
0,004922	13,80226	424,4783	438,2805
0,005060	15,21927	343,9367	359,156
0,005198	16,61708	267,8272	284,4443
0,005336	17,99646	195,7977	213,7941
0,005474	19,35812	127,5321	146,8902
0,005612	20,70272	62,74612	83,44884
0,005750	22,03088	1,183294	23,21418
0,005787	22,38427	-14,8051	7,57916

Rys. 11. Charakterystyka obciążeniowa górotworu

Rys. 12. Powiększony fragment charakterystyki obciążeniowej

3.5.2

USTALENIE OPTYMALNYCH WARUNKÓW OBCIĄŻENIA I ZACISKANIA OBUDOWY.

Z wykresu odczytano u_opt = 0,005729 [m] - punkt przecięcia się dwóch funkcji :

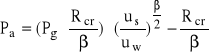
i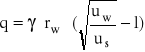

P_min wg PN = q(u_w = u_opt) =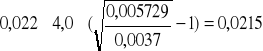
MPa

P_min = q(u_w = u_g) =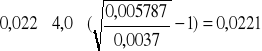
MPa

3.5.3

ANALIZA WPŁYWU PARAMETRÓW GÓROTWORU NA PRZEBIEG CHARAKTERYSTYKI OBCIĄŻENIOWEJ.

Przedmiotem rozważań jest analiza wpływu wielkości Rcg (wytrzymałość na jednoosiowe ściskanie górotworu pierwotnego ) na przebieg charakterystyki obciążeniowej.

Aby to uczynić należy uzależnić któryś parametr występujący w równaniu krzywej od Rcg. Parametrem, który możemy powiązac jest Pg ( oddziaływanie radialne strefy sprężystej).

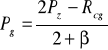
Wpływ wielkości Rcg na Pg

Rcg [MPa]	10,0	15,0	20,0	25,0	31,69	35,0
Pg [Mpa]	6,728	5,523	4,318	3,113	1,436	1,04

Zmieniając wartość Rcg obserwujemy, że wraz ze wzrostem Rcg parametr Pg maleje powodując tym samym zmniejszenie wartości u_w .

3.6

USTALENIE OBCIĄŻEŃ DZIAŁAJĄCYCH NA OBUDOWĘ PROJEKTOWANEGO WYROBISKA KORYTZRZOWEGO

3.6.1

ANALIZA WYNIKÓW PRZEPROWADZONYCH OBLICZEŃ

Optymalne przemieszczenie uopt odczytano z przecięcia się dwóch funkcji P_a i q.

u_opt = 0,005729 [m]

Zasięg strefy plastycznej dla uopt wynosi:

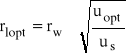
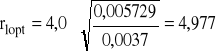
m

P_min wg PN = q(u_w = u_opt) = 0,0215 MPa

P_min = q(u_w = u_g) = 0,0221 MPa

3.6.2

ZESTAWIENIE OBCIĄŻEŃ DZIAŁAJĄCYCH NA OBUDOWĘ W STROPIE I W OCIOSACH WYROBISKA

Porównanie wartości otrzymanych obciążeńi:

• obciążenie pionowe:

wg Cymbarewicza: q_z = 0,0266 MPa

P_min (minimalne oddziaływanie statyczne) = 0,0221 MPa

• Obciążenia poziome na krańcach ociosów wynoszą:

q_x1 = 0,012 Mpa

q_x2 = 0,022 MPa

Różnica między wartościami obciążeń pionowych wynosi tylko 4,5 kPa, co potwierdza słuszność wyboru metody Cymbarewicza do przeprowadzonych obliczeń.

4.

WYTYCZNE DLA SŁUŻB GEOTECHNICZNYCH.

• pobrać próbki materiału skalnego do badań,

• wykonać odwiert w stropie na wysokości wyrobiska (h),

• wykonać odwiert w spągu na głębokość połowy wysokości wyrobiska (0,5h),

• opracować i podać podzielność rdzenia,

• zbadać rozmakalność skał w otoczeniu wyrobiska,

• wykonać badania na jednoosiowe ściskanie skał,

• wyznaczyć kąt tarcia wewnętrznego,

• wykonać badanie na rozciąganie warstwy skał tworzącej strop,

• określić wytrzymałość pozniszczeniową.

Oznaczenia zastosowane w projekcie

- ciężar objętościowy;

- średni ciężar objętościowy;

- współczynnik Poisona skały,

- współczynnik Poisona górotworu,

Φ_g - kąt tarcia wewnętrznego górotworu,

E_g - moduł sprężystości górotworu,

σ_z - naprężenie pionowe,

σ_x - naprężenie poziome,

σ_r - naprężenie radialne,

σ_t - naprężenie statyczne,

R_cs - normowa wytrzymałość skał na ściskanie,

R_rs - normowa wytrzymałość skał na rozciąganie,

E_s - normowy moduł sprężystości skały,

h_o - strzałka sklepienia,

k₀,k_l - współczynniki zależne od podzielności i rozmakalności skał,

R_cr - wytrzymałość resztkowa górotworu uśrednionego,

α_w,β_w - współczynniki opisujące kształt wyrobiska ,

ε_L - względne odkształcenie strefy plastycznej,

ϕ_s - pozorny kąt tarcia wewnętrznego skały,

b - szerokość wyrobiska,

c - spójność,

f - współczynnik zwięzłości skały,

h - miąższość warstwy,

H - głębokość,

H_kr - głębokość krytyczna,

P_a - ciśnienie deformacyjne,

P_g - ciśnienie na granicy w strefie sprężystej i plastycznej,

P_min - minimalne ciśnienie na obudowę,

P_z - ciśnienie pionowe w górotworze nienaruszonym,

r_L - promień sfery plastycznej,

r_Lg - graniczny promień strefy plastycznej,

r_Lopt - optymalny promień strefy plastycznej,

r_w - promień wyrobiska,

u_g - graniczne przemieszczenie konturu wyrobiska,

u_L - przemieszczenie strefy plastycznej,

u_opt - optymalne przemieszczenie konturu wyrobiska,

u_s - przemieszczenie sprężyste konturu wyrobiska,

u_w - przemieszczenie konturu wyrobiska,

5.

LITERATURA

• Polska Norma PN - G - 05020;

• Zdzisław Kłeczek - „Geomechanika górnicza”;

• Zenon Wiłun - „Zarys geotechniki”;

h_o

h

a

a

b

b+2a = b+2h·tg(45-
)

45+

Rys.1 Obciążenie obudowy wyrobiska chodnikowego wg Cymbarewicza

q_z

q_x1

q_x2

Rys. 2. Schemat obciążeń wyrobiska

tg (45-
)

a₁

h_o

h

a₂

b

Rys. 3. Zmodyfikowana teoria Sałustowicza

arctgE

arctgE

R_cr

R_cg

σ

ε

σ₁ = σ₃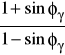
+ R_cg

σ₁ = σ₃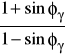
+ R_cr

Rys. 4. Charakterystyka wytrzymałości modelu sprężysto-plastycznego

σ

ε

R_cr

R_cg

τ = σ tg
_g+c^'

τ = σ tg
_g+c

c^'

c

_g

_g

I

II

r_w

r_l

Pa

q

Pz

Rys. 5. Osiowo - symetryczny układ stref wokół wyrobiska korytarzowego

Pg

P_g

r_lg

Pa = f (r_l)

q

q =f (r_L)

r

u_w

u_l

r_w

r_l

P_a

P_g

Rys.9. Zaciskanie się wyrobiska

P_g

P_v = P_a +q

P_a

P_min

P_min

(wg PN)

q

u_s

u_g

u_opt

u_w

---