REGRESJA LINIOWA

Współczynnik REGRESJI - określa charakter współzależności liniowej dwóch zmiennych (2 cech); mówi o ile zmieni się (wzrośnie lub zmaleje) zmienna zależna (cecha y), jeżeli zmienna niezależna (cecha x) zmieni się (wzrośnie) o jedną jednostkę (kg, l, cm itp.). Zmienna zależna powinna mieć rozkład normalny.

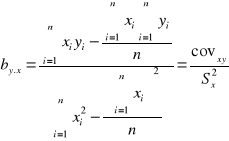
gdzie:

x - zmienna niezależna

y - zmienna zależna

i = 1, 2, 3, ..., n

n - liczba par obserwacji

Oszacowane równanie PROSTEJ REGRESJI:

Wartość parametru a:

KORELACJA (Pearson'a)

Współczynnik KORELACJI - podobnie jak współczynnik regresji jest miarą zależności, przy czym określa stopień (siłę) zależności liniowej dwóch zmiennych (2 cech). Przyjmuje wartości w granicach od -1 do 1, przy czym 0 oznacza brak zależności.

Warunkiem stosowania korelacji Pearson'a jest rozkład normalny obu badanych cech.

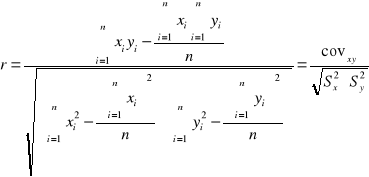
Przyjmuje się, że gdy:

|r| = 1 ⇒ korelacja ZUPEŁNA

|r| ≥ 0,7 ⇒ korelacja WYSOKA

0,4 < |r| < 0,7 ⇒ korelacja ŚREDNIA

|r| ≤ 0,4 ⇒ korelacja NISKA

r = 0 ⇒ brak korelacji

Przykład:

Badano straty masy ciała kur (Y) w zależności od odległości (X), na jaką je przewożono. W tabeli podano masę ciała kur po transporcie (kg) i odległość (km):

X (km):	35	29	26	40	50
Y(kg):	3,0	3,6	3,2	2,8	2,4

Napisz równanie prostej regresji Y na X. Zinterpretuj współczynnik regresji. Określ stopień współzależności liniowej.

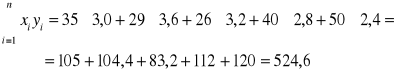
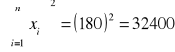
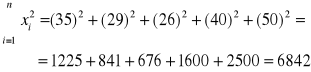
Współczynnik REGRESJI:

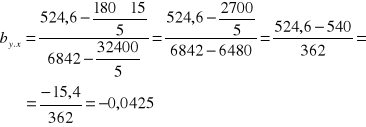
Wyraz wolny:

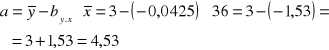
Równanie prostej regresji:

Interpretacja współczynnika regresji:

Jeżeli odległość, na jaką przewożone są kury, wzrośnie o 1 km to ich masa ciała zmniejszy się o 0,0425 kg.

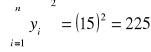
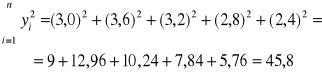
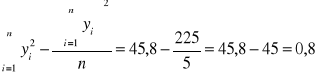
KORELACJA - stopień zależności liniowej:

Istnieje WYSOKA zależność między masą ciała kur, a odległością na jaką je transportowano.

Zadanie 1:

Mierzono wysadność wełny (X) i wydajność (Y) u maciorek merynosa polskiego. Uzyskano następujące wyniki:

X:

6,50;

6,90;

7,20;

7,00

Y:

4,50;

4,52;

5,10;

4,90

Napisz równanie regresji Y na X i zinterpretuj oszacowany współczynnik regresji. Określ stopień zależności liniowej badanych cech.

Zadanie 2:

Badano zależność przyrostów masy ciała królików (Y) od zużytej paszy (X). Na podstawie poniższych wyników oblicz współczynnik regresji Y na X oraz określ korelację między ilością skarmianej paszy, a masą ciała.

X:	5	3	1	4
Y:	10	7	5	9

Zadanie 3:

Współczynnik regresji wydajności mlecznej na długość odstępu międzywycieleniowego wynosi 5,22 kg. Oblicz prawdopodobną wydajność krowy o długości odstępu międzywycieleniowego równej 378 dni, gdy średnio okres ten trwa 368 dni, a średnia wydajność mleczna wynosi 3650 kg.

Zadanie 4:

Badano zużycie paszy (X) i masę ciała u kurcząt (Y). Na podstawie poniższych wyników napisz równanie prostej regresji Y na X oraz podaj interpretację otrzymanego współczynnika.

X:

18;

20;

12;

10;

15

Y:

8;

5;

5;

4;

7

zmienna zależna

współczynnik regresji

(wsp. kierunkowy prostej)

zmienna niezależna

wyraz wolny (stała regresji)

n = 5

---