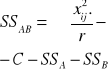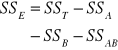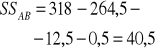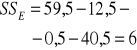DWUCZYNNIKOWA ANALIZA WARIANCJI
Ten typ analizy wariancji służy do weryfikacji hipotezy o równości średnich w przypadku, gdy na badaną cechę X wpływa jednocześnie jeden z poziomów A1, A2, ..., Aa czynnika A oraz jeden z poziomów B1, B2, ..., Bb czynnika B.
Hipotezę zerową weryfikujemy na podstawie wyników prób o jednakowej liczbie powtórzeń r w ab populacjach.
czynnik |
B1 |
B2 |
... |
Bb |
suma obserwacji w wierszach |
B A |
|
|
|
|
|
A1 |
|
|
... |
|
x1.. |
A2 |
|
|
... |
|
x2.. |
... |
... |
... |
... |
... |
... |
Aa |
|
|
... |
|
xa.. |
suma obserwacji w kolumnach |
x.1. |
x.2. |
... |
x.b. |
suma wszystkich obserwacji x... |
Ai - poziomy czynnika A (i = 1, 2, 3, ... a)
Bj - poziomy czynnika B (j = 1, 2, 3, ... b)
k - numer obserwacji (k = 1, 2, 3, ... r)
a - liczba poziomów czynnika A (liczba wierszy)
b - liczba poziomów czynnika B (liczba kolumn)
r - liczba powtórzeń
xijk - k-ta obserwacja w j-tej kolumnie i i-tym wierszu
xij• - suma obserwacji w i-tym wierszu i j-tej kolumnie
N = a x b x r - liczba wszystkich obserwacji
INTERAKCJA - polega na równoczesnej, niejednakowej reakcji poziomów jednego czynnika na zmianę poziomów drugiego czynnika.
sposób nawożenia A |
brak interakcji |
INTERAKCJA |
||||||
|
odmiany zboża B |
|||||||
|
b1 |
b2 |
b1 |
b2 |
||||
a1 |
15 |
+4 |
11 |
+4 |
15 |
+4 |
11 |
+7 |
a2 |
19 |
|
15 |
|
19 |
|
18 |
|
Hipotezy zerowe i alternatywne:
hipoteza zerowa dotycząca wpływu czynnika A:
H0: brak wpływu czynnika A na badaną cechę
HA: czynnik A wpływa na badaną cechę
hipoteza zerowa dotycząca wpływu czynnika B:
H0: brak wpływu czynnika B na badaną cechę
HA: czynnik B wpływa na badaną cechę
hipoteza zerowa dotycząca INTERAKCJI:
H0: brak interakcji
HA: występuje interakcja
MODEL LINIOWY - analiza wariancji w układzie dwuczynnikowym:
![]()
Yijk - wartość obserwacji
μ - średnia populacji
αi - efekt czynnika doświadczalnego A
βj - efekt czynnika doświadczalnego B
(αβ)ij - efekt interakcji (A∗B)
εijk - błąd losowy (błąd próby)
Tabela analizy wariancji:
Źródło zmien.: |
df stopnie swobody |
SS suma kwadratów |
MS średni kwadrat (wariancja) |
ogólna |
dfogólna = N-1 |
|
- |
czynnik A |
dfA = a-1 |
|
|
czynnik B |
dfB = b-1 |
|
|
interakcja A∗B |
dfA*B =(a-1)(b-1) |
|
|
błąd |
dfbłąd = dfogólna - dfA - dfB - dfA*B |
|
|
Wartość statystyki testowej:
dla INTERAKCJI:
![]()
Jeżeli interakcja okaże się istotna bądź wysoce istotna, to kończymy analizę na tym etapie !!!
Jeżeli interakcja okaże się nieistotna, to obliczamy FA i FB, aby określić wpływ czynników A i B:
Podejmowanie decyzji:
F0,05 F0,01
Poprawka:
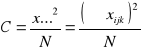
Przykład:
Badano przydatność do tuczu dwóch ras królików, stosując dwa rodzaje dawek pokarmowych o różnej wartości odżywczej: pełnowartościową mieszankę A i mieszankę B o zredukowanej zawartości białka. W tabeli podano przyrosty królików. Sprawdź, czy występuje interakcja między rasą, a sposobem żywienia oraz określ wpływ badanych czynników na wielkość uzyskanych przyrostów.
dawka rasa |
A |
B |
xi.. |
Biała Nowozelandzka |
5; 8
|
2; 3
|
18 |
Czarna Podpalana |
4; 5
|
9; 10
|
28 |
x.j. |
22 |
24 |
x... = 46 |
![]()
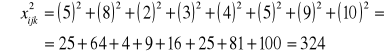
![]()
![]()
![]()
Źródło zmienności: |
df |
SS |
MS |
ogólna |
|
|
- |
czynnik A (między rasami) |
|
|
|
czynnik B (między dawkami) |
|
|
|
interakcja A∗B |
|
|
|
błąd |
|
|
|
![]()
F0,05 (df1 = 1, df2 = 4) = 7,71
F0,01 (df1 = 1, df2 = 4) = 21,2
Zadanie 1:
Badano wpływ trzech różnych dawek pokarmowych na przyrosty kurcząt obu płci. Uzyskane wyniki przedstawiono w tabeli. Sprawdź, czy istnieje interakcja między dawkami, a płcią kurcząt. Zbadaj wpływ rozpatrywanych czynników na przyrosty.
dawka płeć |
A |
B |
C |
KURKI |
3; 3; 4 |
6; 5; 5 |
7; 10; 11 |
KOGUTKI |
2; 4; 2 |
6; 7; 8 |
10; 9; 12 |
Zadanie2:
Przeprowadzono doświadczenie, którego celem było zbadanie wpływu witaminy B12 i pewnego antybiotyku na przyrosty świń. Zwierzęta podzielono na dwie grupy. Każda grupa poddawana była innej kombinacji obu czynników. W tabeli podano średnie dzienne przyrosty świń w funtach. Sprawdź, czy wystąpiła interakcja między czynnikami i oszacuj istotność ich wpływu na uzyskane wyniki.
antybiotyk (μg) |
witamina B12 (μg) |
||
|
0 |
50 |
|
0 |
1,30 1,19 1,08 |
1,26 1,21 1,19 |
|
40 |
1,05 1,00 1,05 |
1,52 1,56 1,55 |
|
Zadanie 3:
Badano wpływ sezonu (letni, zimowy) oraz rasy na grubość słoniny u tuczników. Wyniki przedstawiono w poniższej tabeli. Oszacuj istotność wpływu badanych czynników. Zbadaj, czy zachodzi między nimi interakcja.
rasa sezon |
WBP |
PBZ |
PUŁ |
letni |
5; 7; 6 |
4; 2; 3 |
2; 3; 1 |
zimowy |
4; 2; 5 |
2; 3; 5 |
2; 2; 3 |
1
X11•
X12•
X1b•
X21•
X22•
X2b•
Xa1•
Xa2•
Xab•
dla czynnika B:
![]()
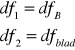
dla czynnika A:
![]()
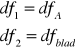
brak podstaw do odrzucenia H0
F0 <F0,05
brak istotnych różnic
F0,05 ≤ F0∗ < F0,01
różnice istotne
F0,01 ≤ F0∗∗
różnice wysoce istotne
odrzucamy H0 na rzecz HA
Σ=13
Σ=5
Σ=9
Σ=19
F0 > F0,05 i F0 >F0,01 ⇒ odrzucamy H0
na rzecz HA, interakcja jest wysoce istotna - kończymy analizę.
Wyszukiwarka
Podobne podstrony:
ANOVA hierarch odp folia Word2003, Elementy matematyki wyższej
1-czyn ANOVA odp folia Word2003, Elementy matematyki wyższej
ANOVA hierarch odp folia Word2003, Elementy matematyki wyższej
korelacja regresja Word2003, Elementy matematyki wyższej
Hierarchiczna analiza wariancji zadania Word2003, Elementy matematyki wyższej
ściąga Word2003, Elementy matematyki wyższej
test chi kwadrat Word2003, Elementy matematyki wyższej
Jednoczynnikowa analiza wariancji zadania Word2003, Elementy matematyki wyższej
1-czyn ANOVA odp folia Word2003 uzupełnione, Elementy matematyki wyższej
1.2.2 Bity i bajty, 1.2 Elementy matematyki
Zadania geograficzne z elementami matematyki, Edukacja wczesnoszkolna, ED.PRZYRODNICZA, różne zadani
Elementy matematyki
Elementy matematyki finansowej 2014
1.2.6 Zamiana 8-bitowych liczb dwójkowych na liczby dziesiętne, 1.2 Elementy matematyki
Zadania geograficzne z elementami matematyki 2, Nauka, Pomoce dydaktyczne, Zadania
24.02.2008 ELEMENTY MATEMATYKI FINASOWEJ, Ekonomia
1.2.1 Dwójkowa rebrezentacja danych, 1.2 Elementy matematyki
1.2.10 Adresy IP i maski sieci, 1.2 Elementy matematyki
wzrastająca ilość elementów, matematyka
więcej podobnych podstron