Nagłe pękanie.

Jeśli wyobrazimy sobie gumowy balonik (guma w napompowanym baloniku jest rozciągana w 2 kierunkach), w którym jest małą dziurka, to w zależności od stopnia napompowania będziemy mieli:

a/ balonik, który jest napompowany niewielkim ciśnieniem, z którego uchodzi przez nieszczelność powietrze, ale balonik jest cały;

b/ przy zwiększaniu stopnia napompowania (czyli ciśnienia wewnętrznego) powłoka balonu w pewnym momencie gwałtownie pęka.

Nagłe pękanie.

Jak wspominano w rozdziale o naprężeniach w zbiornikach ciśnieniowych, w powłoce zbiornika kulistego i w części walcowej walcowego zbiornika ciśnieniowego panują naprężenia błonowe (rozciąganie dwukierunkowe) - jeśli zbiornik obciążony jest głownie nadciśnieniem od strony wklęsłej.

Modelem naprężeń błonowych w powłoce jest powłoka balonika gumowego napełnionego np. gazem pod pewnym nadciśnieniem. Jej grubość jest dużo mniejsza od innych wymiarów. Jeśli taki zbiornik będziemy powoli napełniać np. gazem, i obserwować jego wielkość, to dojdziemy do takiego stanu napełnienia ( ciśnienia wewnętrznego) że dalsze jego zwiększanie spowoduje pęknięcie balonika. Będzie to świadczyło Jeśli w takim zbiorniku przed jego napełnieniem wykonamy szpilką otwór, to balonik nasz będzie podczas napełniania gazem “syczał” , sygnalizując stan nieszczelności , a przy pewnej wielkości nadciśnienia balonik nagle pęknie, pomimo że naprężenia w powłoce były dużo niższe niż w powłoce bez “dziurki”.

Nagłe pękanie występuje czasem w konstrukcjach rzeczywistych, pomimo że zostały one zaprojektowane poprawnie pod względem tak wielkości naprężeń jak i odkształceń. Zjawisko nagłego pękania występuje najczęściej w konstrukcjach spawanych jak kadłuby statków, mosty, zbiorniki ciśnieniowe czy rurociągi. W konstrukcjach tych, na skutek nieuniknionych błędów w spawaniu, występują pęknięcia. Wzrost tych pęknięć, z szybkością równą szybkości dźwięku w materiale, to właśnie nagłe pękanie.

Nagłe pękanie zwiazane jest z uwalnianiem energii: jeśli praca wykonana przez ciśnienie wewnętrzne i energia sprężysta wyzwolona podczas pękania są mniejsze od energii “rozdarcia powłoki” - “rozdarcie” nie nastąpi, czyli pękniecie powłoki jest stabilne. Dopiero przekroczenie tej energii powoduje powstanie niestabilności i rozdarcie powłoki zbiornika.

Można napisać równanie energii, jakie musi być spełnione, aby nastąpiło nagłe pękanie:

gdzie:

G_c - stała materiałowa tzw. wiązkość materiału [J/m²];

t - grubość materiału [m];

- przyrost wielkości pęknięcia [m];

a - początkowa wielkość pęknięcia [m];

- zmiana energii sprężystej [J];

- praca obciążenia [J].

Po odpowiednich przekształceniach warunek można zapisać w postaci:

gdzie:

naprężenia w materiale w momencie nagłego pękania;

a - początkowa wielkość pęknięcia [m];

E - moduł Younga dla materiału [J/m²];

G_c - wiazkość materiału [J/m²] (N/m).

Bardzo często powyższa zależność jest zapisywana w postaci :

K = K_c

Gdzie:

K =
- współczynnik intensywności naprężeń [MN/m^-3/2];

K_c=
- krytyczny współczynnik intensywności naprężeń [MN/m^-3/2]; zwany też współczynnikiem K_c (po angielski : fracture tonghness).

Gdy grubość płyty i jej długość oraz szerokośc są dużo większe od wielkości pęknięcia
a , wtedy należy zastosować zależność:

K=

Uwaga : w przypadku dokładnej analizy zjawiska pękania w innym przypadku niż płyta o wspomnianych wymiarach, należy w literaturze poszukiwać dokładniejszych zależności.

Tab. 1. Wiązkość G_c i krytyczny współczynnik intensywności naprężeń K_c.

Lp.	Materiał	Gc	Kc
		[kJ/m^2]	[MN m^-3/2]
	Czyste , plastyczne metale jak Al,Cu, Ag	100-1000	100-350
	Stale o wysokiej wytrzymałości	15-118	50-154
	Miękkie stale węglowe (niskowęglowe)	100	140
	Żywice epoksydowe wzmacniane włóknem szklanym	40-100	42-60
	Stopy aluminium	8-30	23-45
	Drewno, pękanie prostopadłe do włókien	8-20	11-13
	Stale o średniej zawartości węgla	13	51
	PP	8	3
	LDPE	6-7	1
	HDPE	6-7	2
	ABS	5	4
	nylon	2-4	3
	Beton wzmacniany stalą (żelbet)	0,2-4	10-15
	żeliwo	0,2-3	6-20
	Polistyren (PS)	2	2
	Węglik krzemu SiC	0,05	3
	Beton niezbrojony	0,03	0,2
	marmur	0,02	0,9
	Szkło sodowe	0,01	0,7-0,8
	Porcelany elektrotechniczne	0,01	1
	lód	0,003	0,2

Pękanie zbiornika ciśnieniowego.

1.Zbiornik kulisty.

Jak pokazano w części dotyczącej naprężeń w ściankach zbiornika, naprężenia w zbiorniku kulistym w obu kierunkach są równe i wynoszą:

a naprężenia zastępcze (błonowe - zgodnie z teorią Hubera):

Maksymalne naprężenia, jakie można dopuścić to

Natomiast przy nagłym pękaniu

stąd

i można określić krytyczną wielkość pęknięcia przy naprężeniach równych granicy plastyczności R_e:

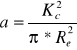
dla miękkiej stali węglowej niskiej jakości R_e=200 [MN/m²]; K_c=140[MN m^-3/2]

i otrzymamy a=155,9 mm

dla stali kotłowej R_e=275 [MN/m²]; K_c=140[MN m^-3/2] otrzymamy:

a=82.4 mm

dla jakościowej stali na zbiorniki ciśnieniowe R_e=1000 [MN/m²];

K_c=170 [MNm^-3/2] otrzymamy a =9,1mm

Dla zbiornika ze stopu aluminium R_e=400 [MN/m²]; K_c=25[MN m^-3/2]

a =1 mm

Tab.2 wielkość szczeliny a[mm] wywołującej naprężenia równe granicy plastyczności

Lp	Materiał	Re [MN/m^2]	Kc [MN m^-3/2]	a [mm]
1.	Miękka stal węglowa	200	80	50,9
2.	Stal St3 normalizowana	240	25	3,4
3.	Stal kotłowa	275	100	42
4.	Stal jakościowa na zbiorniki	1000	170	9
5.	Stal A533 na zbiorniki ciśnieniowe	350	120	37
4.	Stal o wysokiej wytrzymałości	1000	80	2
4.	Stop aluminium AlCuMg	450	27	1,1
5.	Miedź	60	150	1990
6.	LDPE (PE małej gęstości)	20	1	0,8
7.	HDPE (PE wysokiej gęstości)	30	2	1,4
8.	Żywica epoksydowa wzmocniona włóknem szklanym (GFRP) (dane przybliżone)	100	45	65
9.	Szkło sodowe	3600	0.8	1,5*10^-5

Z obliczeń widać, że miękka i plastyczna miedź jest praktycznie odporna na pękanie. To samo dotyczy stali niskowęglowych (stal miękka i kotłowa). Już jakościowa stal na zbiorniki ma graniczny wymiar szczeliny wielkości 9 mm a stal o wysokiej wytrzymałości - 2 mm. Nieciągłość o wymiarze 2 mm może zostać dość łatwo niezauważona w czasie badań (zdjęcia RTG czy badania ultradźwiękowe). Podobnie jest ze stopem aluminium , dla którego graniczna wielkość szczeliny wynosi 1 mm. Podobnie małe nieciągłości są niebezpieczne dla polietylenu, przy czym PE dużej gęstości (HDPE) jest bardziej odporny (a=1,4 mm) niż LDPE (a=0,8 mm). Szkło sodowe, mimo bardzo wysokiej wartości granicy plastyczności ma bardzo niską wartość K_c i krytyczna wielkość szczeliny a =1,5*10^-5 mm!

Aby zapewnić bezpieczeństwo zbiornika należy tak dobrać materiał, aby przed pęknięciem zbiornik uległ rozszczelnieniu, czyli pękniecie o wielkości równej grubości ścianki zbiornika było bezpieczne ze względu na pękanie.

Przykładowe obliczenia wielkości a =g podano w tab2..

Wyznaczona w tabeli 2 wielkość pęknięcia a jest wielkością krytyczna - pękniecie większe niż a przy działaniu odpowiednio dużych naprężeń staje się niestabilne i z bardzo dużą szybkością (zbliżoną do prędkości dźwięku w materiale) powiększa się, powodując gwałtowne zniszczenie elementu (katastrofę). Patrząc w dane zawarte w tabeli 1 można zauważyć, że są materiały charakteryzujące się dużymi wartościami K_c i G_c są bardzo odporne na zjawisko nagłego pękania, inne - posiadające niższe parametry K_c i G_c są mniej odporne.

Mechanizmy rozwoju pęknięć.

W elemencie z materiału plastycznego, zawierającym pęknięcie, wywołanie nagłego pęknięcia jest bardzo trudne. Jeśli doprowadzimy do tego i obejrzymy przekrój pęknięci, da się łatwo zauważyć dużą chropowatość przełomu. Świadczy to o znacznych odkształceniach plastycznych w przekroju pęknięcia. Te znaczne odkształcenia plastyczne materiału ( płyniecie materiału) w strefie pękania powoduje ”stępienie ostrza pękania”, czyli zwiększenie promienia strefy o podwyższonych naprężeniach, przy jednoczesnym obniżeniu ich wartości. W strefie tej jest pochłaniana duża ilość energii związana z plastycznym odkształceniem materiału. Pochłanianie dużej ilości energii jest równoznaczne z wysokimi wartościami K_c i G_c

W materiałach takich jak ceramika lub twarde stale mechanizm pękania jest inny. Przełom w łupliwym materiale nie jest chropowaty, lecz gładki. Granica plastyczności R_e tych materiałów jest wysoka, więc strefa uplastycznienia przed ”ostrzem pękania” jest małą i mała też jest energia odkształcenia plastycznego pochłaniana w strefie pękania. Pękanie następuje gwałtownie. W ten sposób pęka szkło, materiały ceramiczne , wysokowęglowe stale (zwłaszcza w temperaturach poniżej zera)i inne metale o sieciach RPC i HZ ( regularna przestrzennie centrowana i heksagonalna zwarta). Właściwie jedynie metale o sieci RSC (regularna ściennie centrowana) jak miedź, aluminium czy ołów nie stają się kruche w niskich temperaturach.

Ten sposób pękania jest charakterystyczny również dla polimerów. Polimery w temperaturze poniżej tzw. temperatury zeszklenia T_G. Poniżej tej temperatury polimer zachowuje się jak ciało stałe.

Kompozyty ( w tym drewno) cechują się większą odpornością na pękanie od polimerów bez wypełnienia. Dodanie do polimeru włókien ( szklanych węglowych czy borowych) znacznie zwiększa odporność na pękanie, pomimo że same włókna też nie wykazują wysokiej odporności na pękanie. Mechanizm tego jest prosty. Gdy pękniecie zbliża się do włókna, powoduje oddzielanie się włókna od polimeru (tzw. delaminację), co chwilowo zwiększa wymiar pęknięcia i tym samym „stępią ostrze” pęknięcia. Dzieje się tak przy każdym włóknie. Jeśli naprężenia i pękanie są skierowane wzdłuż włókien - mechanizm ten nie funkcjonuje ( przykład: pękanie drewna wzdłuż i w poprzek słojów). Również dodatek wypełniaczy do polimerów powoduje wzrost ich odporności na pękanie ( np. ABS - gdzie wypełniaczem są cząsteczki gumy).

1

---