PODPOWIEDZI DO ZADAŃ Z ZESTAWU 6

Zad.3. a) i b) - banalne, w c) czeka całka podwójna
, co oznacza najpierw całkowanie ... po dx, a następnie tego wyniku - po dy. A co to jest ... to trzeba sobie narysować.

Zad.4. Tutaj jest smaczek całki potrójnej!

Zad.5. Po pierwsze: rysunek, na którym w układzie XY umieszczamy masy m₁ i m₂. Skoro środek układu ma być w środku masy, więc trzeba obliczyć położenie SM. Wówczas masa m₁ jest w odległości r₁ od OO, masa m₂ w odległości r₂ czyli znane są współrzędne obu mas co jak się okaże jest niezbędne do obliczeń składowych tensora I.

Skoro moment pędu L jest wektorem, to na podstawie rysunku możemy zapisać jego składowe jako:

L_x= ω⋅I_xx ; L_y= ω⋅I_xy ; L_z= ω⋅I_xz (dlaczego takie składowe tensora I ?).

Reszta jest liczeniem.

Zad.7. a1) Kulka się toczy, a zatem ma dwa rodzaje energii kinetycznej.

a2) Jej środek masy porusza po okręgu o promieniu .... z prędkością kątową Ω = dφ/dt i prędkością liniową V = Ω⋅(R-r). Znając zależność między prędkością kątową i liniową można więc obliczyć energię kinetyczną z a):

E_k =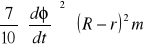

a3) przy porządnym rysunku widać, że energia potencjalna kulki: E_p = mg(R-r)(1-cosφ)

b) Wyrazy współczucia dla nie lubiących liczyć pochodnych, ale za to otrzymujemy równanie:

i zakładając, że sinφ ≈ φ

otrzymujemy równanie typowe dla ruchu harmonicznego:
gdzie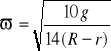

Jego rozwiązaniem jest odpowiednia funkcja φ(t), która wstawiona do wyrażenia na V daje nam końcową odpowiedź na c).

I to by było na tyle. Z.Sz.

---