W.W.NiG	Laboratorium z Hydromechaniki	Grupa 5/4
Data przeprowadzenia cwiczenia: 29.05.2006r.	TEMAT Wyznaczenie bezwymiarowego współczynnika oporu lokalnego ξ.	Zespół w składzie: Karczewski Grzegorz Boniecki Łukasz Kołodziejski Radosław
Data oddania sprawozdania:	Uwagi	ocena

AKADEMIA GÓRNICZO - HUTNICZA

im. Stanisława Staszica

w Krakowie

1.Cel ćwiczenia:

Celem ćwiczenia jest doświadczalne wyznaczenie bezwymiarowego współczynnika oporu

skupionego ξ. Przedmiotem pomiarów jest nagłe przewężenie przewodu o stałej średnicy.

2.Podstawy teoretyczne:

Podczas przepływu płynu występują straty ciśnienia na oporach zwanych lokalnymi lub miejscowymi. Na oporach lokalnych następują zmiany kierunków oraz modułów wektorów prędkości. Zawirowania powodują straty energii większe od tych, które występują podczas przepływu przez odcinek prostoosiowy. Wielkość straty ciśnienia na oporze lokalnym wynosi

gdzie :

ξ = ξ(Re) - bezwymiarowy współczynnik oporu lokalnego odniesiony zazwyczaj do prędkości za przeszkodą

v - średnia prędkość w przekroju odniesienia (zazwyczaj za przeszkodą).

Wartość współczynnika ξ określa się eksperymentalnie. Wielkość ξ zależy od kształtu elementu wywołującego opór, prędkości przepływu, gęstości i lepkości płynu.

Przy przepływie laminarnym współczynnik ξ maleje ze wzrostem liczby Reynoldsa, natomiast przy w pełni rozwiniętym przepływie turbulentnym ma wartość stałą.

Rozważa się przepływ płynu o gęstości ρ przez poziome połączone ze sobą szeregowo przewody kołowe

Między przewodami 1 i 2 znajduje się opór lokalny. Starta ciśnienia na rozważanym odcinku jest sumą strat liniowych oraz straty na oporze lokalnym. Strata ciśnienia na oporze liniowym jest równa:

Strata ciśnienia na oporze lokalnym wynosi

3.Pomiary:

Dokonaliśmy następujących pomiarów:

d=27mm, l₁=17cm, l₂=19,5cm, l₃=49cm, l₄=38,5cm

, T_s = 21,5°C, T_w = 14,0°C, p = 732 mmHg.

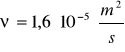
dla d = 27 mm

Δh1 [m]	Δh2 [m]	ΔPd [Pa]
0,014	0,012	83
0,017	0,015	102
0,02	0,018	120
0,022	0,02	140
0,025	0,024	169
0,029	0,027	189
0,031	0,029	200
0,034	0,032	222
0,036	0,034	238
0,039	0,036	255

Dla d = 20 mm

Δh1 [m]	Δh2 [m]	ΔPd [Pa]
0,024	0,022	45
0,033	0,029	64
0,043	0,039	83
0,057	0,054	104
0,072	0,068	130
0,079	0,076	143
0,094	0,09	170
0,105	0,102	186
0,127	0,124	230
0,145	0,14	260

Dla d = 15 mm

Δh1 [m]	Δh2 [m]	ΔPd [Pa]
0,046	0,044	24
0,063	0,063	33
0,081	0,082	41
0,102	0,103	51
0,12	0,12	59
0,132	0,132	65
0,155	0,155	75
0,182	0,182	87
0,2	0,201	99
0,229	0,23	110

Dla d = 13 mm

Δh1 [m]	Δh2 [m]	ΔPd [Pa]
0,029	0,031	12
0,044	0,046	18
0,06	0,062	23
0,069	0,071	27
0,083	0,086	30
0,106	0,101	36
0,134	0,137	47
0,172	0,177	59
0,195	0,201	62
0,245	0,25	110

4.Obliczenia

Obliczenia zostały wykonane według poniższych wzorów:

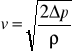
5. Wnioski

Po przeprowadzonym doświadczeniu możemy stwierdzić, że mamy do czynienia z przepływem turbulentnym, gdyż współczynnik oporu skupionego ξ zmienia się nieznacznie, w porównaniu do liczba Reynoldsa.

5

---