OPORY RUCHU W PRZEWODACH POD CIŚNIENIEM

1.Wrowadzenie teoretyczne

Ciecz rzeczywista jest lepka, a więc podczas przepływu pokonuje opory tarcia kosztem energii mechanicznej. Ubytek tej energii wyrażony jest stratami ciśnienia między dwoma poprzecznymi strumieniami cieczy. Straty proporcjonalne do długości przewodu to opory liniowe h_L, natomiast nagłe straty ciśnienia są to opory miejscowe h_m .

Opory miejscowe mogą być wywołane przez armaturę na przewodzie, przez zmiany kierunku ruchu, zmiany przekroju poprzecznego przewodu. Wartość tych oporów wyrażona jest wzorem:

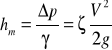
(1.1)

gdzie:

∆p - różnica ciśnień przed i za przeszkodą,

γ - ciężar objętościowy przepływającej cieczy,

ξ  - współczynnik oporów miejscowych ,

V  średnia prędkość cieczy za przeszkodą

Wartości współczynników miejscowych wyznaczane są doświadczalnie i podane w tablicach. Zależą one od liczby Reynoldsa:

(1.2)

gdzie:

μ - dynamiczny współczynnik lepkości, cieczy

ρ - gęstość cieczy,

ν - kinematyczny współczynnik lepkości cieczy,

Q - objętościowe natężenie przepływu,

D - średnica wewnętrzna przewo

Opory liniowe zależą od rodzaju ruchu opisanego liczbą Reynoldsa. Dla obu rodzajów ruchu (laminarnego i turbulentnego) λ uzależniona jest od:

• w ruchu laminarnym λ=λ((Re)

• w ruchu turbulentnym:

a.) strefa gwałtownego wzrostu oporów liniowych

b) strefa rur hydraulicznie gładkich λ=λ(Re)

c) strefa przejściowa λ=λ((Re,ε)

d) strefa kwadratowej zależności oporów λ=λ(ε)

gdzie
, k - bezwzględna chropowatość przewodu.

Opory liniowe w przewodach pod ciśnieniem oblicza się ze wzoru Darcy - Weisbacha:

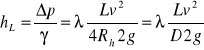
(1.3)

gdzie:

λ - współczynnik oporów liniowych,

L - długość przewodu,

v - średnia prędkość,

D - średnica przewodu,

Rh- promień hydrauliczny

F- pole przekroju poprzecznego strumienia,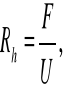
U-obwód zwilżony przekroju

2. Wykonanie ćwiczenia

Dane modelu :

•długość odcinków pomiarowych do pomiaru λ 7,20 m

•długość odcinków pomiarowych do pomiaru λ

-przewód plastikowy Ø 13 mm 3,25 m

•średnice przewodów ze stratami lokalnymi 16 mm

•długość odcinków pomiarowych do pomiaru ς 2,40 m

•średnice przewodu z piezometriami 16, 20, 26, 20, 16 mm

Dane odczytane z tablic:

•gęstość wody w przewodzie (przy 9,5)=282,65K ρ= 999,7 kg/m^{3 ,}

•gęstość wody w manometrze (przy 20,5°C) = 293,65 K ρ'= 997,99 kg/m^{3 ,}

•gęstość cieczy manometrycznej (przy 20,5˚C)=293,65K ρ_cm =13543,5 kg/m^{3 ,}

•kinematyczny współczynnik lepkości dla T=283 K, ν=

Opory liniowe

Po przekształceniu wzoru nr.1.3 otrzymaliśmy następujący wzór:

(2.1)

gdzie:

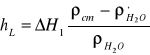
(2.2)

ΔH - różnica wskazań manometru różnicowego m Hg,

ρ_cm - gęstość cieczy manometrycznej (przy 20,5˚C) kg/m^3,

ρ' - gęstość wody w manometrze (przy 20,5˚C) kg/m³ ,

ρ - gęstość wody w przewodzie (przy 9,5˚C) kg/m³

(2.3)

gdzie:

Q - natężenie przepływu regulowane przez rotametr m³/s,

D - średnica badanego przewodu m

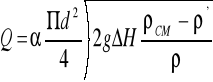
(2.4)

ΔH- różnica poziomów rtęci w manometrze,

d- średnica otworu kryzy pomiarowej, d=14,2 mm,
,

ρ_cm - gęstość cieczy manometrycznej,

ρ' - gęstość wody w manometrze,

ρ - gęstość wody w przewodzie,

α- liczba przepływu α=α(ΔH)

Po dokonaniu niezbędnych przekształceń otrzymaliśmy wzór o następującej postaci:

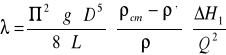
(2.5)

Współczynnik oporów liniowych zależy od ruchu, który opisywany jest liczbą Reynoldsa wzorem:

Re =
=
(2.6)

gdzie:

v - średnia prędkość przepływu cieczy m/s ,

ν - kinematyczny współczynnik lepkości m²/s,

D - średnica badanego przewodu m

Przykładowe obliczenia dla przewodu plastikowego o średnicy D=16mm =0,016m; L=7,20m (dla pomiaru nr1 )

1. ∆H1 = h_p - h_l m

∆H1 = [325-(-275)]/1000=0,6

2. ∆H = H_p - H_l m

∆H=[71-(-105)]/1000=0,176 m

3. wysokość oporów liniowych wyliczono ze wzoru (2.2)

h_L = 0,6
= 7,529 m

4. natężenie przepływu wody wyznaczono ze wzoru (2.4)

Q=0,738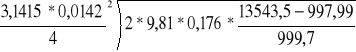
=
m³/s

5. średnią prędkość przepływu wyliczono ze wzoru (2.3)

v=
m/s

6. współczynnik oporów liniowych wyliczono ze wzoru (2.5)

λ =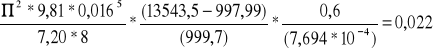

• liczbę Reynoldsa wyliczono ze wzoru (2.6)

Re=
--> [Author:S]

Opory miejscowe

Badanie oporów miejscowych ζ przeprowadziliśmy korzystając z przewodu plastikowego o średnicy D= 16 mm z układem czterech kolan. Opory te są spowodowane przez: armaturę zainstalowaną na przewodzie, zmiany kierunku ruchu, zmiany przekroju poprzecznego przewodu. Badania przeprowadziliśmy analogicznie do pomiarów oporów liniowych. Wyniki przedstawiliśmy w tabeli.

Współczynnik oporów miejscowych ζ wyznacza się ze wzoru określającego opory całkowite h_c:

h_{c =} h_{L +} h_m

gdzie:

h_L - opór liniowy,

h_m -oór miejscowy

Podstawiając wzory nr(2.1) i nr(2.3) otrzymujemy:

h_c =

(2.8)

Przekształcając wzór otrzymujemy:

gdzie:

ξ - współczynnik oporów miejscowych,

g - przyspieszenie ziemskie m/s^2,

D - średnica przewodu m,

L₂ - długość badanego odcinka przewodu m,

h_c - całkowita wysokość oporów miejscowych m

h_c = ∆h₂
(2.8a)

gdzie:

ρ_cm - gęstość cieczy manometrycznej kg/m^3,

ρ` - gęstość wody w manometrze kg/m^3,

ρ - gęstość wody w przewodzie kg/m^3,

∆h₂ - różnica wskazań manometru mHg,

V -średnia prędkość przepływu m/s

V =
[m/s] (2.9)

gdzie:

Q - natężenie przepływu regulowane przez rotametr m³/s,

D - średnica badanego przewodu m

3.Wyniki pomiarów, tablice, wykresy

Tablica(3.1) dla przewodu plastikowego o średnicy D=16 mm i długości L=7,20 m

Lp.	[mm]	[mm]	[m]	[mm]	[mm]	[m]	[m]	[-]	Q		V	Re
1	-275	325	0,6	-105	71	0,176	7,53	0,738	0,000769	0,023	3,802	46882
2	-265	300	0,565	-100	65	0,165	7,09	0,739	0,000743	0,023	3,698	45307
3	-235	274	0,509	-90	55	0,145	6,39	0,74	0,000698	0,023	3,471	42530
4	-217	247	0,464	-80	51	0,131	5,82	0,74	0,000663	0,023	3,300	40424
5	-200	225	0,425	-75	45	0,12	5,33	0,744	0,000638	0,023	3,175	38899
6	-180	202	0,382	-68	39	0,107	4,79	0,746	0,000604	0,023	3,006	36831
7	-155	175	0,33	-60	30	0,09	4,14	0,747	0,000555	0,024	2,761	33824
8	-130	150	0,28	-50	25	0,075	3,51	0,75	0,000509	0,024	2,530	31001
9	-107	125	0,232	-40	17	0,057	2,91	0,753	0,000445	0,026	2,215	27134
10	-85	100	0,185	-33	12	0,045	2,32	0,754	0,000396	0,026	1,971	24141
11	-60	75	0,135	-25	7	0,032	1,69	0,757	0,000335	0,027	1,668	20438
12	-50	50	0,1	-10	0	0,01	1,25	0,76	0,000188	0,062	0,936	11471

Tablica (3.2) dla przewodu stalowego o średnicy D=21 mm i długości L=7,20

Lp.	[mm]	[mm]	[m]	[mm]	[mm]	[m]		[m]	[-]	Q		V	Re
1	30	300	0,27	-140	95	0,235	3,39		0,728	0,000874	0,030	2,524	40583
2	44	282	0,238	-130	82	0,212	2,99		0,73	0,000832	0,030	2,404	38652
3	65	275	0,21	-110	75	0,185	2,64		0,732	0,000779	0,030	2,252	36206
4	80	265	0,185	-107	70	0,177	2,32		0,733	0,000763	0,027	2,205	35462
5	100	260	0,16	-100	70	0,17	2,01		0,734	0,000749	0,025	2,164	34802
6	105	240	0,135	-80	50	0,13	1,69		0,737	0,000658	0,027	1,900	30557
7	110	225	0,115	-60	30	0,09	1,44		0,742	0,000551	0,033	1,592	25598
8	115	212	0,097	-55	15	0,07	1,22		0,748	0,00049	0,035	1,415	22758
9	125	205	0,08	-45	20	0,065	1,00		0,749	0,000473	0,031	1,366	21959
10	131	190	0,059	-40	11	0,051	0,74		0,75	0,000419	0,029	1,211	19477
11	145	185	0,04	-30	5	0,035	0,50		0,753	0,000349	0,028	1,007	16200
12	165	160	0,005	-10	-5	0,005	0,06		0,76	0,000133	0,024	0,384	6180

Tablica (3.3) dla przewodu stalowego skorodowanego o średnicy D=21 mm i długości L=7,20 m

lp.	[mm]	[mm]	[m]	[mm]	[mm]	[m]	[m]	[-]	Q		V	Re
1	-230	285	0,515	-100	65	0,165	6,46	0,736	0,00074	0,081	2,138	34379
2	-200	260	0,46	-85	55	0,14	5,77	0,738	0,000684	0,085	1,975	31754
3	-185	245	0,43	-80	50	0,13	5,40	0,74	0,000661	0,085	1,908	30682
4	-150	220	0,37	-70	40	0,11	4,64	0,741	0,000608	0,086	1,758	28261
5	-140	200	0,34	-65	35	0,1	4,27	0,743	0,000582	0,086	1,680	27019
6	-110	175	0,285	-50	25	0,075	3,58	0,747	0,000506	0,096	1,463	23525
7	-80	150	0,23	-45	20	0,065	2,89	0,748	0,000472	0,089	1,364	21930
8	-50	120	0,17	-35	10	0,045	2,13	0,75	0,000394	0,094	1,138	18296
9	-38	100	0,138	-20	0	0,02	1,73	0,752	0,000263	0,171	0,761	12230
10	5	75	0,07	-18	-4	0,014	0,88	0,754	0,000221	0,123	0,638	10259
11	22	55	0,033	-12	-8	0,004	0,41	0,758	0,000119	0,202	0,343	5513
12	27	45	0,018	-10	-5	0,005	0,23	0,76	0,000133	0,088	0,384	6180

Tablica (3.4) dla przewodu plastikowego o średnicy D=16 mm z oporem miejscowym(układ 4 kolan) i długości L=2,40 m

Lp.	[mm]	[mm]	[m]	[mm]	[mm]	[m]	[m]	[-]	Q		V		Re
1	-300	300	0,6	-80	50	0,13	7,53	0,738	0,000659	0,031	1,903	36,212	30599
2	-280	275	0,555	-75	45	0,12	6,96	0,74	0,000635	0,030	1,833	36,092	29478
3	-270	250	0,52	-70	40	0,11	6,53	0,74	0,000608	0,031	1,755	36,890	28223
4	-250	220	0,47	-60	30	0,09	5,90	0,743	0,000552	0,034	1,594	40,424	25632
5	-200	180	0,38	-50	25	0,075	4,77	0,745	0,000505	0,033	1,459	39,009	23462
6	-185	150	0,335	-40	20	0,06	4,20	0,75	0,000455	0,036	1,314	42,416	21126
7	-170	125	0,295	-35	15	0,05	3,70	0,751	0,000416	0,038	1,201	44,703	19311
8	-145	100	0,245	-30	10	0,04	3,07	0,753	0,000373	0,039	1,077	46,161	17318
9	-115	60	0,175	-27	6	0,033	2,20	0,758	0,000341	0,033	0,985	39,441	15834
10	-90	35	0,125	-20	0	0,02	1,57	0,758	0,000265	0,039	0,767	46,484	12327
11	-60	0	0,06	-15	0	0,015	0,75	0,76	0,00023	0,025	0,666	29,593	10704
12	-35	-30	0,005	-10	-5	0,005	0,06	0,76	0,000133	0,006	0,384	7,398	6180

Obserwacja piezometrycznej linii ciśnień

			D=20mm		D=26mm		D=20mm		D=16mm
pomiar	Q	p2[mm]	p1[mm]	p2[mm]	p1[mm]	p2[mm]	p1[mm]	p2[mm]	p1[mm]	p2[mm]
1	0,00025	1076	1025	1038	1005	975	930	830	710	540

5.Rachunek błędów

• Błąd λ

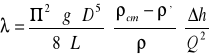
Wielkościami obarczonymi błędem są: ∆Q=
m³/s

∆(∆h)=1 mm=0,001 m

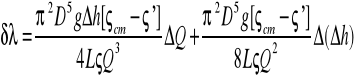
Przykładowe obliczenia dla przewodu plastikowego o średnicy D=16 mm,

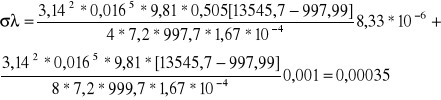
nr	∆ H [m]	Q [m3/s]	hL	λ	V [m/s]	błąd
1	0,6	0,000769	7,53	0,023	3,802	0,00318
2	0,565	0,000743	7,09	0,023	3,698	0,00080
3	0,509	0,000698	6,39	0,023	3,471	0,00035
4	0,464	0,000663	5,82	0,023	3,300	0,00020
5	0,425	0,000638	5,33	0,023	3,175	0,00013
6	0,382	0,000604	4,79	0,023	3,006	0,00009
7	0,33	0,000555	4,14	0,024	2,761	0,00006
8	0,28	0,000509	3,51	0,024	2,530	0,00005

• Błąd Re:

Wielkościami obarczonymi bęłdem są: ∆Q = ∆Q=
m³/

∆ν = 0,040 m²/s

Re=

przykładowe obliczenia dla przewodu plastikowego D= 16 mm

= 1295

6.Wnioski

W pierwszej części ćwiczenia laboratoryjnego wyznaczaliśmy wartość współczynnika oporu liniowego λ dla trzech rodzajów rur o długości 7200mm. Obliczone wartości współczynnika λ oscyluje wokół pewnej wartości i nie ma tak widocznego spadku. Spowodowane jest to z całą pewnością błędami pomiarowymi a przede wszystkim nieuwagą przeprowadzających badania.Wraz ze spadkiem natężenia spada liczba Reynoldsa

Kolejnym doświadczeniem była obserwacja piezometrycznej linii ciśnień. Na podstawie sporządzonego wykresu zauważyliśmy, że na przewodzie (o zmiennych średnicach) mimo takiego samego natężenia przepływu na początku i końcu przewodu o tej samej średnicy wysokość słupa wody jest różna. Wnioskujemy, że spowodowane jest to stratami ciśnienia na długości przewodu oraz stratami miejscowymi.

10

---