Cel ćwiczenia to zapoznanie się z:

• Metodyką wykonywania pomiarów nadciśnienia statycznego

• Zasada działania manometrów mechanicznych i cieczowych

• Zagadnienia wpływu położenia manometru mechanicznego na odczytywanie wartości

• Problemem zakresu mierniczego i klasy urządzenia

• Analizą błędów i określaniem wartości średniej małej liczby pomiarów za pomocą narzędzi statycznych

Zakres ćwiczenia obejmuje:

• Pomiar nadciśnienia w przewodzie za pomocą manometrów mechanicznych (M2, M3,M4) i cieczowego (M1)

• Pomiar nadciśnienia za pomocą manometru mechanicznego (M4) dla kilku wybranych wariantów zniesienia manometru względem osi przewodu

• Określenie gęstości cieczy manometrycznej

• Przeanalizowanie wpływu zakresu mierniczego i klasy urządzenia na błędy pomiarowe

• Określenie wartości nadciśnienia z małej liczby pomiarów, za pomocą narzędzi statystycznych

Manometr (ciśnieniomierz)jest miernikiem służącym do pomiaru ciśnienie cieczy i gazów. Ciśnienie mierzone jest w odniesieniu od ciśnienie odniesienia. Ciśnieniem odniesienia jest ciśnienie atmosferyczne, natomiast miernik pokazuje wartość, o jaką ciśnienie mierzone jest niższe lub wyższe od danego ciśnienia atmosferycznego (tj. nadmiarowy przyrząd pomiarowy).

Manometry cieczowe składają się z dwóch naczyń połączonych napełnionych cieczą manometryczną. Najczęściej są to syntetyczne oleje lub rtęć. Zasada działania urządzeń polega na przemieszczaniu się cieczy manometrycznej. Ruch ten wynika z dążenia do ustalenia równowagi pomiędzy mierzonym ciśnieniem a ciśnieniem cieczy w manometrze. W praktyce pomiar ten polega na odczytaniu położenia cieczy na podziałce wyskalowanej w odpowiednich jednostkach ciśnienia (najczęściej Pascale, milimetry słupa wody lub milimetry słupa rtęci).

Zasada działania manometrów sprężystych opiera się na pomiarze odkształcenia elementu sprężystego pod wpływem mierzonego ciśnienia. Kształt naczyń sprężystych jest tak dobrany, aby mierzone odkształcenie s było liniową funkcją ciśnienia p. Najbardziej rozpowszechnione są manometry sprężyste z rurka Burdona.

Manometr jest podstawowym miernikiem stosowanym w: ciepłownictwie, gazownictwie, energetyce cieplnej, wodociągach i kanalizacji, przemyśle spożywczym, hydraulice i hydraulice siłowej, rolnictwie.

Opis stanowiska

Układ składa się z poziomego przewodu stalowego, zasilanego z sieci wodociągowej poprzez zbiornik hydroforowy. Do przewodu stalowego podłączone są następujące urządzenia:

• Manometr cieczowy M1

• Manometr mechaniczny M2, klasa 1,6

• Manometr mechaniczny M3, klasa 0,4

• Manometr mechaniczny M4, klasy 0,4 -zainstalowany z możliwością zmiany poziomu położenia

• Termometr

Tabele pomiarów

Manometr	Klasa	Zakres
M	0,4	do 10 kG/cm^2
M2	1,6	do 0,6 MPa
M3	0,4	do 6 kG/cm^2
M4	0,4	do 2,5 bar

Obliczanie błędów pomiarów urządzeń

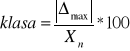
• dla manometru M

• dla manometru M2

• dla manometru M3

• dla manometru M4

Tabele wyników pomiarów

Pomiar 1

M	M1	M2	M3	M4
[KG/cm^2]	[mm]	[MPa]	[KG/cm^2]	[bar]	Wysokość [m]
1,2	435	0,115	1,17	1,19	-0,5
1,16	0
1,06	0,5
1,01	1

Pomiar 2

M	M1	M2	M3	M4
[KG/cm^2]	[mm]	[MPa]	[KG/cm^2]	[bar]	Wysokość [m]
1,0	367	0,1	1,0	0,85	1
0,9	0,5
0,95	0
1,0	-0,5

Pomiar 3

M	M1	M2	M3	M4
[KG/cm^2]	[mm]	[MPa]	[KG/cm^2]	[bar]	Wysokość [m]
0,86	330	0,085	0,91	0,88	-0,5
0,84	0
0,80	0,5
0,76	1

Pomiar 4

M	M1	M2	M3	M4
[KG/cm^2]	[mm]	[MPa]	[KG/cm^2]	[bar]	Wysokość [m]
0,65	242	0,065	0,68	0,5	1
0,57	0,5
0,62	0
0,68	-0,5

Pomiar 5

M		M1		M2		M3		M4
[KG/cm^2]	[mm]		[MPa]		[KG/cm^2]		[bar]		Wysokość [m]
0,41	150		0,04		0,41		0,42		-0,5
0,38		0
0,34		0,5
0,3		1

Obliczanie gęstości cieczy manometrycznej ;)

Z powodu błędnego odczytu wartości różnicy wysokości słupów cieczy manometrycznej w manometrze różnicowym obliczenie gęstości cieczy okazuje się zadaniem niemożliwym.

Ujednolicamy jednostki na MPa oraz sprowadzamy do jednakowego poziomu pomiarów (do osi rury).Następnie obliczamy wartość średnią z małej liczby pomiarów, za pomocą narzędzi statystycznych.

-nadciśnienie, które wskazywał manometr

h -wysokość manometru nad oś rury (zmierzona wynosi 9cm dla manometrów M2, M3, dla M4 wysokość podana jest w tabelach powyżej )

Wartość średnia pomiarów

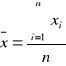
n- ilość pomiarów -6

Niepewność przypadkowa wartości średniej

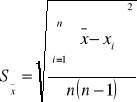
Przyjęliśmy przedział ufności równy
=0,9 ,
=2,015

Odchylenie standardowe

Przedział ufności

Pomiar 1

M [MPa]	M2 [MPa]	M3 [MPa]	M4 [MPa]
0,1177	0,1159	0,1156	0,1141
			0,1160
			0,1109
			0,1108

Wartość średnia
=0,1139 MPa

Niepewność przypadkowa wartości średniej
=0,0010 MPa

Odchylenie standardowe
=0,0020 MPa

Przedział ufności

Pomiar 2

M [MPa]	M2 [MPa]	M3 [MPa]	M4 [MPa]
0,0981	0,1009	0,0989	0,0948
			0,0949
			0,0950
			0,0951

Wartość średnia
=0,0966 MPa

Niepewność przypadkowa wartości średniej
=0,0011MPa

Odchylenie standardowe
=0,0022 MPa

Przedział ufności

Pomiar 3

M [MPa]	M2 [MPa]	M3 [MPa]	M4 [MPa]
0,0843	0,0859	0,0901	0,0831
			0,0840
			0,0849
			0,0858

Wartość średnia
=0,0856MPa

Niepewność przypadkowa wartości średniej
=0,0010 MPa

Odchylenie standardowe
=0,0020 MPa

Przedział ufności

Pomiar 4

M [MPa]	M2 [MPa]	M3 [MPa]	M4 [MPa]
0,0637	0,0659	0,0676	0,0598
			0,0619
			0,0620
			0,0631

Wartość średnia
=0,0634 MPa

Niepewność przypadkowa wartości średniej
=0,0012 MPa

Odchylenie standardowe
=0,0024 MPa

Przedział ufności

Pomiar 5

M [MPa]	M2 [MPa]	M3 [MPa]	M4 [MPa]
0,0402	0,0409	0,0411	0,0371
			0,0380
			0,0389
			0,0398

Wartość średnia
=0,0393 MPa

Niepewność przypadkowa wartości średniej
=0,0006 MPa

Odchylenie standardowe
=0,0013 MPa

Przedział ufności

Wnioski:

• Czym większa klasa i zakres urządzenia tym błąd pomiaru jest większy.

• Najdokładniejszym urządzeniem okazał się manometr M4.

---