Sprawozdanie z wykonanego ćwiczenia nr 401 |
|
|
|
Temat: |
WYZNACZENIE WSPÓŁCZYNNIKA ŚWIATŁA ZA POMOCĄ REFRAKTOMETRU ABBEGO. |
|
|
Imię i nazwisko: |
Anna Napiecek Sylwia Afshin-Rad |
|
|
WTM |
Semestr: III |
Rok: II |
|
Zespół: 6 |
Data wykonania: 1993.10.17 |
Ocena: |
Podpis: |
WYZNACZANIE WSPÓŁCZYNNIKA ŚWIATŁA ZA POMOCĄ REFRAKTOMETRU ABBEGO.
Na granicy dwóch ośrodków izotropowych ![]()
i ![]()
, w których światło rozchodzi się z różnymi prędkościami ![]()
i ![]()
, promień świetlny wchodzący z ośrodka ![]()
do ośrodka ![]()
zmienia kierunek swojego biegu. Jeżeli np. wiązkę promieni świetlnych skierujemy z powietrza na powierzchnię wody , wówczas część promieni świetlnych ulegnie odbiciu , a część wejdzie do wody , tworząc tzw. wiązkę załamaną. Doświadczalnie stwierdzono , że jeżeli ośrodek ![]()
jest optycznie rzadszy od ośrodka 2, wówczas kąt załamania jest mniejszy od kąta padania oraz ![]()
. Gdy zaś o środek ![]()
jest optycznie gęstszy od ośrodka 2 , promień załamuje się od prostopadłej i wówczas ![]()
oraz ![]()
.
Stałą wartość stosunku sinusów kątów padania i załamania), równą stosunkowi prędkości rozchodzenia się światła w ośrodkach ![]()
i ![]()
, nazywamy współczynnikiem załamania ośrodka ![]()
względem ośrodka ![]()
i oznaczamy przez ![]()
.
![]()
![]()
Obok współczynnika załamania światła charakterystyczną wielkością każdego ośrodka jest jego dyspersja optyczna. Miarą dyspersji danego ośrodka jest różnica współczynników załamania dla linii F i C Fraunhofera , przy czym linia F leży w krótkofalowej części widma , linia C w długofalowej :
![]()
![]()
Zdolność łamiącą danego ośrodka charakteryzuje współczynnik załamania ![]()
dla żółtej linii Fraunhofera ![]()
. Stosunek :
![]()
![]()
naywano zdolnością rozszczepiającą względną danego ośrodka. Pomiar kąta granicznego może być wykorzystany do wyznaczania współczynnika załamania. Jeżeli mierzymy kąt graniczny ![]()
przy przechodzeniu światła z ośrodka badanego o nieznanym współczynniku załamania ![]()
do ośrodka o współczynniku znanym ![]()
, to szukany współczynnik
![]()
![]()
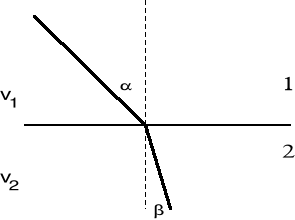
Rys.1.Załamanie światła na pograniczu dwu ośrodków: ![]()
. Promień padający , załamany i normalny do granicy ośrodków wystawiona w punkcie padania, leżą w jednej płaszczyźnie. Stosunek sinusa kąta padania do sinusa kąta załamania równy jest stosunkowi prędkości fazowej ![]()
światła w ośrodku pierwszym do prędkości fazowej ![]()
światła w ośrodku drugim.
TABELA 1
NUMER POMIARU |
|
|
|
|
|
1 |
2 |
3 |
|
1 |
1,3322 |
1,3322 |
1,3323 |
1,33223 |
2 |
1,4547 |
1,4546 |
1,4546 |
1,45469 |
3 |
1,3269 |
1,3270 |
1,3271 |
1,327 |
4 |
1,4856 |
1,4858 |
1,4856 |
1,4856 |
5 |
1,4545 |
1,4544 |
1,4543 |
1,4544 |
TABELA 2
NUMER POMIARU |
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
|
|
|
1 |
42 |
42 |
42,1 |
42,03 |
1,33223 |
0,02473 |
0,03225 |
0,006 |
2 |
41 |
41,2 |
41,2 |
41,13 |
1,45469 |
0,02428 |
0,02902 |
0,008 |
3 |
41 |
41 |
40,5 |
40,83 |
1,327 |
0,02477 |
0,03242 |
0,009 |
4 |
43 |
43 |
43 |
43 |
1,4856 |
0,02419 |
0,02743 |
0,007 |
5 |
42 |
42 |
42 |
42 |
1,4544 |
0,02428 |
0,02902 |
0,007 |

Wyszukiwarka
Podobne podstrony:
400 401
MaxCom KXT 401
Promieniowce l5212013083 id 401 Nieznany
03 47 401 BHP
401 Manuskrypt przetrwania
401, MOJE 401, Sprawozdanie z wykonanego ćwiczenia nr 401
401, #01, 95-11-10
401, 401A1, Sprawozdanie z wykonania ćwiczenia nr 414
401, FIZ401, REMIGIUSZ MAJ Gr.1 Zesp˙˙ : 3
401, FIZ401, REMIGIUSZ MAJ Gr.1 Zesp˙˙ : 3
401,451 401-sprawozdanie
401
Jung Archetypy i symbole s 401 427
401,451, 401
401
401
401,451 401
więcej podobnych podstron