Zestaw 2

1. druga zasada Newtona. Siłą tarcia. Współczynnik tarcia statycznego i kinetycznego

2. wyprowadzenie wzoru na okres wahadła matematycznego

1.

II zasada dynamiki: Jeżeli na ciało działa niezrównoważona siła, to ciało porusza się ruchem zmiennym. Przyspieszenie w tym ruchu jest wprost proporcjonalne do działającej siły, a odwrotnie proporcjonalne do masy ciała. (wzór a=F/M | a). Jeżeli na ciało działa kilka sił, wówczas siła F jest ich wypadkową.

Tarcie

Siły kontaktowe, o których mówiliśmy są normalne (prostopadłe) do powierzchni. Istnieje jednak składowa siły kontaktowej leżąca w płaszczyźnie powierzchni. Jeżeli ciało pchniemy wzdłuż stołu to po pewnym czasie ciało to zatrzyma się. Z drugiej zasady dynamiki wiemy, że jeżeli ciało porusza się z przyspieszeniem to musi działać siła. Taką siłę nazywamy siłą tarcia.

Rozważmy np. klocek, do którego przykładamy "małą" siłę F tak, że klocek nie porusza się. Oznacza to, że sile F przeciwstawia się siła tarcia T. Mamy więc: T = -F. Zwiększamy stopniowo siłę F aż klocek zaczyna się poruszać. Im gładsza powierzchnia tym szybciej to nastąpi. Oznacza to, że siła tarcia zmienia się od wartości zero do pewnej wartości krytycznej w miarę wzrostu siły F. Oznaczmy tę krytyczną siłę T_s (s-statyczna). To jest maksymalna siła tarcia statycznego.

T_s (dla pary powierzchni suchych) spełnia dwa prawa empiryczne:

• Jest w przybliżeniu niezależna od powierzchni zetknięcia (w szerokim zakresie),

• Jest proporcjonalna do siły normalnej (prostopadłej) z jaką jedna powierzchnia naciska na drugą.

Stosunek siły T_s do nacisku F_N nazywamy współczynnikiem tarcia statycznego μ_s

Uwaga: Mówimy tylko o wartościach tych sił bo są one do siebie prostopadłe. Jeżeli F jest większe od T_s to klocek poruszy się, ale będzie istniała siła tarcia T_k (k - kinetyczna) przeciwstawiająca się ruchowi.

Siła T_k spełnia trzy prawa empiryczne:

• Jest w przybliżeniu niezależna od powierzchni zetknięcia (w szerokim zakresie),

• Jest proporcjonalna do siły normalnej (prostopadłej) z jaką jedna powierzchnia naciska na drugą,

• Nie zależy od prędkości względnej poruszania się powierzchni.

Istnieje odpowiedni współczynnik tarcia kinetycznego μ_k

(5.2)

Dla większości materiałów μ_k jest nieco mniejszy od μ_s. Np. μ_k ≈ 1 dla opon na jezdni betonowej.

Tarcie jest bardzo złożonym zjawiskiem i wyjaśnienie go wymaga znajomości oddziaływań atomów na powierzchni. Nie będziemy się tym zajmować. Ograniczmy się do zauważenia, że tarcie odgrywa bardzo istotną rolę w życiu codziennym. W samochodzie np. na pokonanie siły tarcia zużywa się około 20% mocy silnika. Tarcie powoduje zużywanie poruszających się części maszyn. Staramy się je zwalczać. Z drugiej strony bez tarcia nie moglibyśmy chodzić, jeździć samochodami, trzymać ołówka, kredy, czy też nimi pisać.

2.

Wahadło proste jest to wyidealizowane ciało o masie punktowej, zawieszone na cienkiej, nieważkiej, nierozciągliwej nici. Kiedy ciało wytrącimy z równowagi to zaczyna się ono wahać w płaszczyźnie poziomej pod wpływem siły ciężkości. Jest to ruch okresowy. Znajdźmy okres tego ruchu.

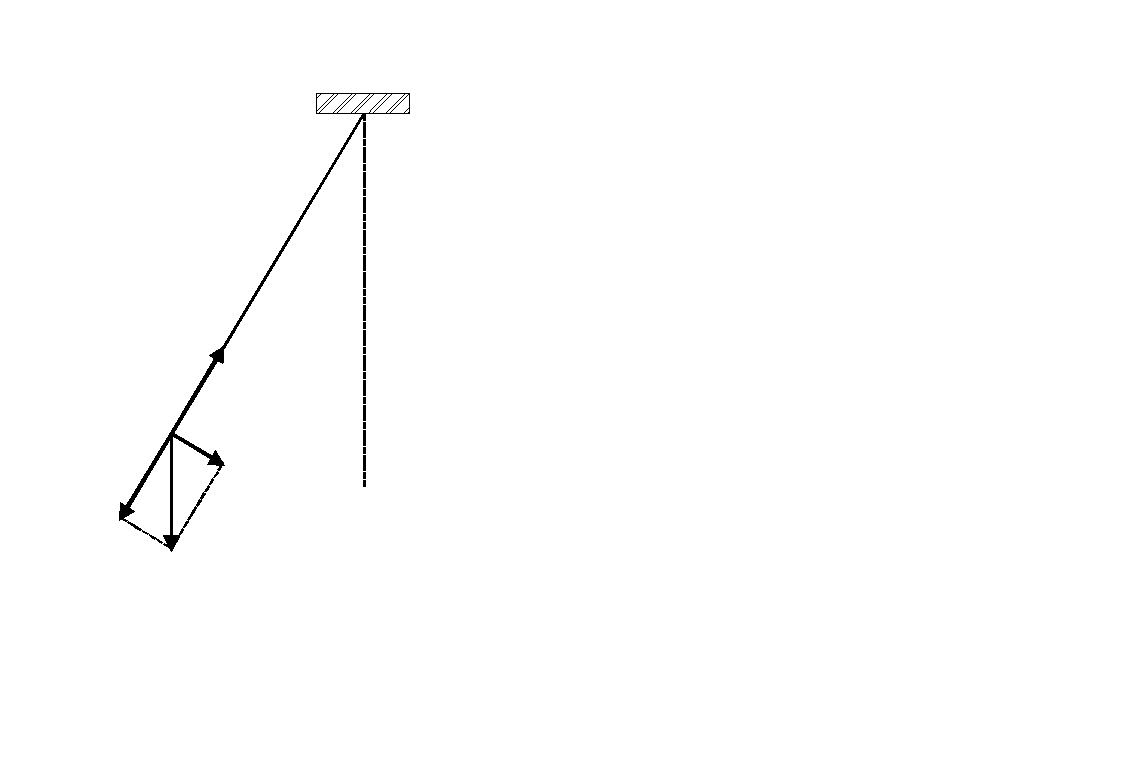
Rysunek przedstawia wahadło o długości l i masie m, odchylone o kąt θ od pionu. Na masę m działają: siła przyciągania grawitacyjnego mg i naprężenia nici N. Siłę mg rozkładamy na składową radialną i styczną. Składowa styczna jest siłą przywracającą równowagę układu i sprowadza masę m do położenia równowagi. Siła ta wynosi: F = mgsinθ. Podkreślmy, że siła jest proporcjonalna do sinθ, a nie do θ, więc nie jest to ruch prosty harmoniczny. Jeżeli jednak kąt θ jest mały (mniejszy niż 10°) to sinθ jest bardzo bliski θ (różnica mniejsza niż 0.5%). Przemieszczenie wzdłuż łuku (z miary łukowej kąta) wynosi x = lθ. Przyjmując zatem, że sinθ ≅ θ otrzymujemy:
. F jest więc proporcjonalna do przemieszczenia (ze znakiem "-"). Jest to kryterium ruchu harmonicznego. Stała mg/l określa stałą k w równaniu F = - kx. Przy małej amplitudzie okres wahadła prostego wynosi więc:
. Zauważmy, że okres wahadła nie zależy od amplitudy i od masy wahadła.

---