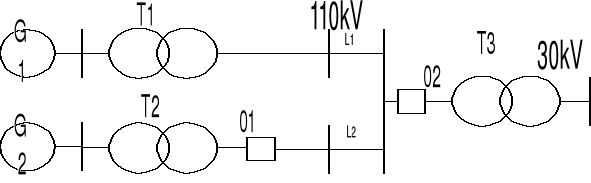
ZADANIE 1

G1:Sn=50MVA,Un=10,5 kV,xd”=12%

G2:Sn=30MVA,Un=6,3 kV,xd”=12%

T1: Sn=50MVA, 10,5/110 kV,Uz=11%

T2: Sn=30MVA, 6,3/110 kV,Uz=10%

T3: Sn=60MVA, 110/30 kV,Uz=11%

L1: x_L'=0,4Ω/km,l1=20km

L2: x_L'=0,4Ω/km,l2=25km

t_z1=1,8s ; t_z2=1,2s - czzasy trwania zwarcia

Punkt zerowy ukł. 110kV jest skutecznie uziemiony

1.War pracy obciążeniowej zwykłej

dla odłączników 01,02 U_ni=110kV

znam I ciągłe I_ob01=S_t2/√3•Un=30000/√3•110=158A

Przyjmujemy wart znormalizowanąI_n01=200A

I_ob02=60000/√3•110=314A; I_n02=400A

2.War pracy zwarciowej

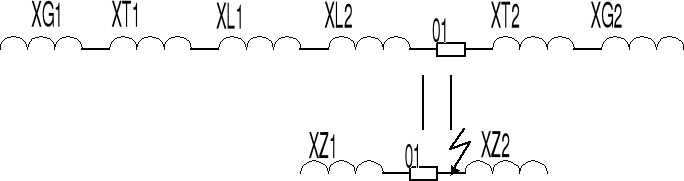
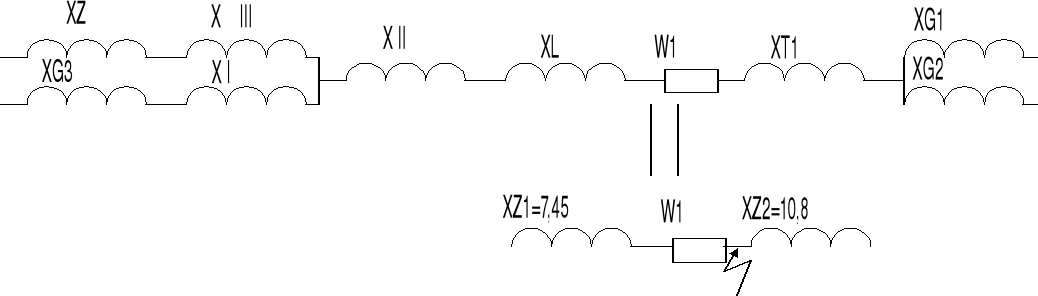
1. dla odłącznika 01

X_G1=(x”_dG1*Un²)/(100*S_G1)=12•110²/100•50=

=29Ω

X_G2=(x”_dG2•Un²)/(100•S_G2)=48,5Ω

X_T1=(uz_T1•Un²)/(100*S_T1)=11•110²/100•50=

26,5Ω

x_L1=x_L'•l1=0,4•20=8Ω, x_L2=0,4*25=10Ω

X_Z1=73,5Ω ; X_Z2=89Ω Ponieważ Xz1<Xz2, cięższe warunki pracy zwarciowej dla odłącznika wystąpią przy zasilaniu ze źródła 1. Punkt zwarcia należy więc założyć w miejscu jak na rys, a dla obliczeń przyjąć Xz1=73,5Ω.

I_K”=1,1U_N/√3*Xz1=1,1*110/√3*73,5=0,95kA

i_p=√2*χ* I_K”=√2*1,8*0,95=2,4kA , χ(kappa)-przyjmujemy 1,8 ,gdyż nie podane.

χ=1,02+0,98e^(-3R/X)=1,8

I_th= I_K”√(m+n)= I_K”=0,95kA

I_1s>=I_th√tz=0,95*√1,8=1,25kA

2. 
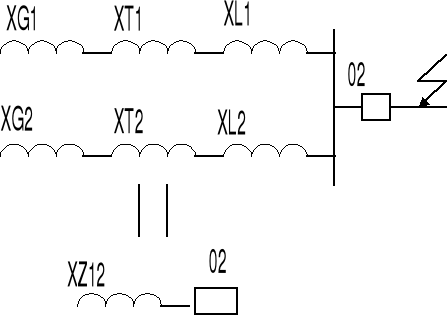
   dla odłącznika 02

Xz1=Xg1+Xt1+Xl1=29+26,5+8=64,5Ω

Xz2=Xg2+Xt2+Xl2=48,5+40,5++10=98,5Ω

Xz=(Xz1*Xz2)/(Xz1+Xz2)=39,5Ω

I_K”=1,1U_N/√3*Xz=1,1*110/√3*39,5=1,8kA

i_p=√2*χ* I_K”=√2*1,8*1,8=4,5kA , χ(kappa)-.

χ=1,02+0,98e^(-3R/X)=1,8

I_th= I_K”√(m+n)= I_K”=1,8kA

I_1s>=I_th√tz=1,8*√1,2=1,25kA

ZADANIE 2

Określ parametry dla warunków pracy normalnej i zwarciowej dla wył W1 i W2

G1,G2:Sn=15MVA, Un =6kV, xd”=12%

G3:Sn=60MVA, Un =10,5kV, xd”=10%

T1: Sn=10MVA, 6/30 kV,Uz=8%

T1: Sn=40MVA, 10,5(I)/30(II)/110(III) kV , UzI-II=8%, UzI-III=16%, UzII-III=10%,

Sz=6000MVA, przy Sn=600MVA

L1: X_L=6Ω ,ODBIÓR O: P=2MW, cos=0,8

1.War pracy obciążeniowej zwykłej

dla wyłączników W1 U_ni=30kV, W2 U_ni=6kV

znam I ciągłe I_obW1=S_t1/√3*Un=10000/√3*30=193A

Przyjmujemy wart znormalizowanąI_nW1=200A

I_obW2=P/√3*Un*cos=2000/√3*6*0,8=242A; I_nW2=400A

2.War pracy zwarciowej

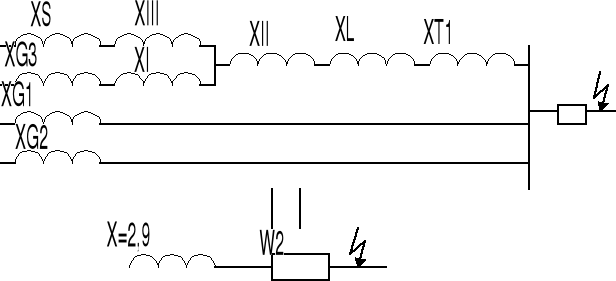
3. dla wyłącznika 01

X_G1=X_G2=(x”_d%*Un²)/(100*S_nG1)=12*30²/100*15=7,2Ω

X_G3=10*30²/(100*60)=1,5Ω

TrafoT2

X_I-II=(uz_I-II*Un²)/(100*S_nT)=8*30²/100*40=1,8Ω

X_I-III=16*30²/100*40=3,6Ω

X_II-III=10*30²/100*40=3,6Ω

X_I=0,5(X_I-II+X_I-III-X_II-III)=0,5(1,8+3,6-2,25)=1,6Ω

X_II=0,5(X_I-II+X_II-III-X_I-III)=0,5(1,8+2,25-3,6)=0,2Ω

X_III=0,5(X_I-III+X_II-III-X_I-II)=0,5(3,6+2,25-1,8)=2Ω

X_L=6Ω

X_S=1,1*U_N²/S_Z=1,1*30²/6000=0,165

DLA W1- t_Z=1,5s t_WW=0,04s

Do obliczeń przyjmujemy Xz1=7,45 Ω jako warunki mniej korzystne

I_K”=1,1U_N/√3*Xz1=1,1*110/√3*7,45=2,55kA

i_p=√2*χ* I_K”=√2*1,8*2,55=6,5kA , χ(kappa)-przyjmujemy 1,8 ,gdyż nie podane.

χ=1,02+0,98e^(-3R/X)=1,8

I_1s>=I_th√tz=2,55*√1,5=3,12kA

I_b=μ* I_K”=1*2,55=2,55kA

Moc wyłączeniowa symetryczna

S_WS=√3*I_b*U_W=√3*2,55*30=135MVA

Przy zwarciach w pobliżu generatora I_b=μ* I_K”

Gdzie μ zależy od t_min (czas między chwilą wystąpienia zwarcia i chwilą pierwszego rozdzielenia styków 1 bieguna łącznika) oraz stosunku I_K”/I_NG. Dla gen SN, gen 1biegunowych oraz kompensatorów synchro:

μ=0,84+0,26e^{-0,26 IKG”/ING} dla t_min=0,02s

μ=0,71+0,51e^{-0,30 IKG”/ING} dla t_min=0,05s

μ=0,62+0,72e^{-0,32 IKG”/ING} dla t_min=0,1s

μ=0,56+0,94e^{-0,38 IKG”/ING} dla t_min=0,25s

w pozostałych przypadkach przyjmuje się μ=1. Wartości I_KG” i I_NG są odniesione do tego samego U. Dla silników ind należy zastąpić I_KG”/I_NG przez I_KM”/I_NM. Jeśli I_KG”/I_NG<=2 to μ=1 dla każdego t_min..

dla wyłącznika W2

DLA W2- t_Z=0,6s t_WW=0,05s

Przyjęto wartości X jak dla 30kV. Dla W2 istnieje tylko 1 możliwość przyjęcia miejsca zwarcia jak na rys.

X_Z6kV= X_Z30kV(6/30)²=2,9*(6/30)²=0,127Ω

I_K”=1,1U_N/√3*Xz1=1,1*6/√3*0,127=30kA

i_p=√2*χ* I_K”=√2*1,8*30=76,5kA , χ(kappa)-przyjmujemy 1,8 ,gdyż nie podane.

χ=1,02+0,98e^(-3R/X)=1,8 I_th= I_K”

I_1s>=I_th√tz=30*√0,6=23,24kA

I_b=μ* I_K”=1*30=30kA

Moc wyłączeniowa symetryczna

S_WS=√3*I_b*U_W=√3*30*6=310MVA

110kV

30kV

6kV

---