35. Wyrównanie obserwacji geodezyjnych metodą spostrzeżeń pośredniczących.

Spostrzeżenia pośredniczące (inaczej pośrednie) występują wtedy gdy nie ma możliwości bezpośredniego pomierzenia szukanych wielkości, musimy wobec tego zadowolić się pomiarem innych wielkości (właśnie pośrednich) związanych funkcjami z wielkościami szukanymi. Przykładowo nie pomierzymy bezpośrednio współrzędnych (szukane) ale możemy pomierzyć kąty i odległości (pośrednie), które są związane funkcjami ze współrzędnymi.

Wspomniane wcześniej funkcje łączą wielkości mierzalne z szukanymi w taki sposób, że wielkości szukane są argumentami a mierzalne wartością funkcji. Zakładamy że funkcje te łączą wielkości prawdziwe (idealne matematycznie) jak też wyrównane. Dzięki temu można skonstruować równania łączące wielkości wyrównane z szukanymi, które nazywa się równaniami poprawek. Wielkości wyrównane (L_i^w) zastępuje się wielkościami obserwowanymi z dodaniem poprawki (L_i+v_i).

zatem mamy:

, gdzie

x,y,z to wielkości poszukiwane (niewiadome)

Bardzo często jednak funkcje f nie są liniowe, dlatego stosuję się linearyzacje równań poprawek. Po co? Trochę trudno było by rozwiązać np. układ 20 równań z czego część jest równaniami kwadratowymi, część logarytmicznymi a cześć ma jeszcze gdzieś pierwiastek...

Linearyzację przeprowadza się wzorami na szereg Taylora. wzór ten wymaga rozwinięcia w otoczeniu pewnego punktu, aby mieć ten punkt stosuje się niewiadome przybliżone (x₀, y₀, z₀), zatem wzór na rownania poprawki ma postać

, gdzie

dx, dy ,dz - przyrosty do niewiadomych - będą faktycznymi niewiadomymi (szukanymi) w procesie wyrównania.

Po linearyzacji okaże się ze mamy tyle równań ile spostrzeżeń pośredniczących a mniej niewiadomych. Dlatego z takiego układu można wyliczyć wiele wariantów wartości niewiadomych. My chcemy jeden wariant najbardziej prawdopodobny (optymalny), dlatego trzeba na układ równań założyć pewien warunek optymalizujący. W tym przypadku metoda najmniejszych kwadratów mówi, że tym warunkiem będzie minimum wartości sumy kwadratów poprawek. Skojarzmy szukanie minimum z zerowanie się pierwszej pochodnej (chyba nie ma sensu ładować tu żadnych wzorów). W zapisie macierzowym operacja ta wygląda tak:

równania poprawek V = A*X+L

równania normalne (A^TA)*X+A^TL=0

Po uwzględnieniu warunku [vv]=min otrzymujemy liniowe równania normalne których jest dokładnie tyle ile niewiadomych, rozwiązujemy je i wyrównanie skończone.

Jest jeszcze analiza dokładności, czyli obliczenie m₀ i błędów niewiadomych z macierzy wariancyjno - kowariancyjnej A^TA.

41. Prawo Gaussa przenoszenia się błędów średnich.

Prawo przenoszenia się błędów pozwoli nam odpowiedzieć na pytanie jaki będzie błąd dowolnej funkcji której błędy argumentów znamy. Prawo to rządzi się znanym wzorem Gaussa:

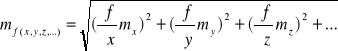
, gdzie

x y z - argumenty funkcji, m_x m_y m_z - błędy tych argumentów

Powyższy wzór działa jednak tylko w sytuacji kiedy argumenty (x, y, z) są zmiennymi losowymi NIEZALEŹNYM, czyli takimi których kowariancja jest równa 0. W przypadku gdyby jednak argumenty nie były niezależnymi zmiennymi losowymi (lub inaczej mówiąc gdyby były skolerowane) należy stosować uogólnione prawo przenoszenia się błędów średnich (prawo kowariancji).

Niech F jest funkcją zmiennych losowych x_1, x_2, x_3, ...

wtedy w na przekątnej macierzy kowariancji M_F pojawią się błędy funkcji

przy czym

M_F = F^T * Cov (X) * F

Cov(X) ma na przekątnej błędy argumentów x_1, x_2, x_3, ... a w pozostałych polach kowariancje tych argumentów, natomiast F to macierz pierwszych pochodnych funkcji F po argumentach x_1, x_2, x_3, ...

(tak z grubsza)

---