Badanie charakterystyki prądowo napięciowej oporników układu

WPROWADZENIE I OGÓLNE PODSTAWY TEORETYCZNE

Opór elektryczny R jest wielkością charakterystyczną dla danego przewodnika. Każdy przewodnik umieszczony w obwodzie prądu stawia przepływowi tego prądu określony dla każdego przewodnika opór elektryczny R. Wielkość oporu określa pierwsze prawo Ohma, które głosi:

dla każdego przewodnika stosunek napięcia U przyłożonego do końców tego przewodnika, do natężenia I płynącego prądu jest wielkością stałą, którą nazywamy oporem elektrycznym R

Badanie charakterystyki prądowo napięciowej opornika R4

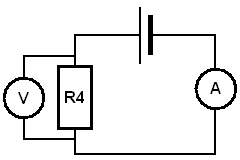
Wyniki zawarte w tabeli zostały obliczane następująco:

∆I=I*0,005+0,01 dla zakresu 20mA

∆U=U*0,015

R=U/I

∆R/R=∆U/U+∆I/I

∆R=∆R/R*R

I [mA]	I±∆I[mA]	U [V]	U±∆U[V]	R [Ω]	∆R/R	R±∆R[Ω]	∆I[mA]	∆U[V]	∆R[Ω]
1,26	1,26±0,02	5,00	5,00±0,08	396,83	0,03	396,83±11,09	0,02	0,08	11,09
1,49	1,49±0,02	6,00	6,00±0,09	402,68	0,03	402,68±10,76	0,02	0,09	10,76
1,81	1,81±0,02	7,00	7,00±0,11	386,74	0,03	386,74±9,87	0,02	0,11	9,87
1,86	1,86±0,02	8,00	8,00±0,12	430,11	0,03	430,11±10,91	0,02	0,12	10,91
2,06	2,06±0,02	9,00	9,00±0,14	436,89	0,02	436,89±10,86	0,02	0,14	10,86
2,24	2,24±0,02	10,00	10,00±0,15	446,43	0,02	446,43±10,92	0,02	0,15	10,92
2,53	2,53±0,02	11,00	11,00±0,17	434,78	0,02	434,78±10,41	0,02	0,17	10,41
2,74	2,74±0,02	12,00	12,00±0,18	437,96	0,02	437,96±10,36	0,02	0,18	10,36
2,99	2,99±0,02	13,00	13,00±0,20	434,78	0,02	434,78±10,15	0,02	0,20	10,15
3,22	3,22±0,03	14,00	14,00±0,21	434,78	0,02	434,78±10,05	0,03	0,21	10,05
3,46	3,46±0,03	15,00	15,00±0,23	433,53	0,02	433,53±9,92	0,03	0,23	9,92

Następnym krokiem jest wykonanie wykresu zależności natężenia od napięcia opornika R4, uwzględniając niepewności pomiarowe i wyznaczając linię trendu.

Wyznaczanie oporów oporników R1, R2, R3.

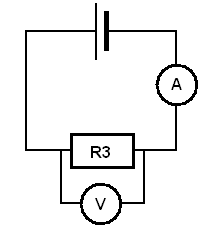
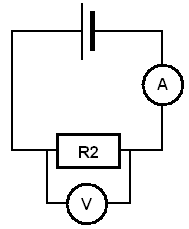
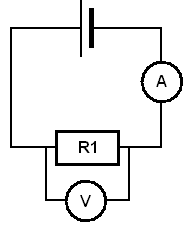
	I [mA]	I±∆I[mA]	U [V]	U±∆U[V]	R [Ω]	∆R/R	R±∆R[Ω]	∆I[mA]	∆U[V]	∆R[Ω]
R1	8,79	8,79±0,05	5,00	5,00±0,08	56,88	0,02	56,88±1,20	0,05	0,08	1,20
R2	4,93	4,93±0,03	5,00	5,00±0,08	101,42	0,02	101,42±2,33	0,03	0,08	2,23
R3	4,93	4,93±0,03	5,00	5,00±0,08	101,42	0,02	101,42±2,33	0,03	0,08	2,23

Wyznaczenie oporu opornika R1 w innym układzie.

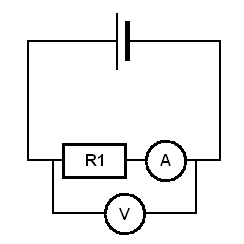
Woltomierz został wpięty równolegle do szeregowego połączenia amperomierza z opornikiem R1.
Z porównania wyników oporów z połączeniem podłączonego woltomierza tylko do opornika R1 bez amperomierza wynika, że opór stanowiący przez amperomierz jest niewielki i nie wpływa on znacząco na wyniki pomiarów oporów, jednakże wyniki
różnią się.

	I [mA]	I±∆I[mA]	U [V]	U±∆U[V]	R [Ω]	∆R/R	R±∆R[Ω]	∆I[mA]	∆U[V]	∆R[Ω]
R1	8,56	8,56±0,05	5,00	5,00	58,41	0,02	58,41±0,02	0,05	0,08	1,24

WNIOSKI DOTYCZĄCE POMIARÓW OPORÓW:

Celem ćwiczenia było zmierzenie oporów poszczególnych oporników w układzie elektrycznym, porównanie tych oporów oraz wyznaczenie błędu pomiarowego. W naszym przypadku opór R1 wynosi 56,88 Ω, R2=101,42 Ω, R3=101,42 Ω. Z tego wynika, że oporniki R2 i R3 są takie same, ponieważ ich opory są sobie równe. Po podłączeniu do opornika R1 amperomierza szeregowo, ten opór uległ w nieznacznym stopniu zmianie. Błędy pomiarowe spowodowane były niedoskonałością przyrządów pomiarowych, błędami ludzkiego oka oraz tym, że ćwiczenie tego typu wykonywaliśmy po raz pierwszy.

---