POLITECHNIKA LUBELSKA
LABORATORIUM METROLOGI
ELEKTRYCZNEJ I ELEKTRONICZNEJ
Ćw. 2 Badanie galwanometru statycznego.
Grupa:
Zespół:
Cel ćwiczenia.
Celem ćwiczenia jest zapoznanie z budową i zasadą działania galwanometru statycznego oraz jego parametrami. Podczas ćwiczenia wyznacza się następujące parametry galwanometru statycznego:
- oporność wewnętrzną Rg
- oporność krytyczną Rkr
- okres wahań nietłumionych To
- stałą prądową Ci
- stałą napięciową Cu
II. Wykonanie ćwiczenia.
Spis przyrządów użytych w ćwiczeniu.
G - galwanometr magnetoelektryczny
Cn = 1,95÷5,22*10-9 A/dz
Rg = 1317 Ω, Rkr = 18000÷1400 Ω
R1 - rezystor R=335 Ω Jmax=0,6 A SN:PL-K-021-E6
R2 - rezystor R=162 Ω Jmax=0,35 A SN:PL-K-043-E6
Rd - rezystor dekadowy Dr6-16=16K Ω kl=0,05
Rn - rezystor wzorcowy RN-1 Jmax=1A R=1 Ω, SN:PL-P3-90-E6
Ogniwo elektrochemiczne 1,27 V
mA - miliamperomierz magnetoelektryczny 0,5A Rw=0,04 Ω
P - przełącznik
Schemat układu pomiarowego.
Rys. 1
Wyznaczanie oporności wewnętrznej galwanometru.
Do wyznaczenia oporności wewnętrznej użyliśmy metody jednakowych odchyleń.
Tabela 1. Rn=1 Ω
Lp. |
Położenie przełącznika |
α dz |
I mA |
Rd1 Ω |
0.5I mA |
Rd2 Ω |
Rg Ω |
Ω |
1 |
lewe |
60 |
5,4 |
16000 |
2,70 |
7300 |
1400 |
1200 |
2 |
lewe |
50 |
4,0 |
14000 |
2,00 |
6400 |
1200 |
|
3 |
prawe |
60 |
5,3 |
16000 |
2,65 |
7500 |
1000 |
|
4 |
prawe |
50 |
3,9 |
14000 |
1,95 |
6400 |
1200 |
|
Przykład obliczenia: ![]()
Wyznaczanie oporności krytycznej galwanometru.
Oporność krytyczną wyznaczaliśmy metodą obserwacji ruchu. W układzie jak na Rys. 1, zakłada się dość dużą rezystancją Rd, aby otrzymać ruch okresowy i wywołuje się dowolne odchylenie wskazówki galwanometru. Następnie wyłącza się źródło prądu i obserwuje, jakim ruchem wskazówka wraca do zera. Jeżeli jest to ruch okresowy, zmniejsza się Rd, i powtarza postępowanie. W ten sposób dochodzi się do stanu, gdy przy pewnej wartości Rd ruch jest jeszcze okresowy, a przy nieznacznym zmniejszeniu Rd staje się nieokresowym. Tę drugą wartość Rd przyjmuje się za oporność krytyczną.
Rn=1 Ω Rg=1317 Ω
Tabela 2
LP |
Położenie przełącznika |
αO dz |
Rd Ω |
Rzkr Ω |
Rkr Ω |
Ω |
1 |
lewe |
64 |
910 |
920 |
2237 |
2292 |
2 |
prawe |
56 |
1020 |
1030 |
2347 |
|
Przykład obliczenia:
![]()
Wyznaczanie stałej prądowej Ci oraz czułości.
Stała prądowa jest to stosunek prądu płynącego przez cewkę galwanometru do ustalonego odchylenia wskazówki. Stała napięciowa jest to stosunek napięcia przyłożonego do galwanometru wraz z opornikiem dodatkowym do ustalonego odchylenia wskazówki.
Tabela 3.
Rn=1 Ω Rg=1317 Ω Rd=2410 Ω
LP |
Położenie przełącznika |
I mA |
α dz |
Ci A/dz |
Sim dz/A |
1 |
lewe |
1,1 |
60 |
5,10*10-9 |
|
2 |
lewe |
0,6 |
30 |
|
|
3 |
prawe |
0,7 |
40 |
4,75*10-9 |
210526315,8 |
4 |
prawe |
0,9 |
50 |
|
|
Przykłady obliczeń:
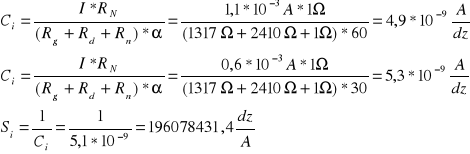
III. Wnioski
W punkcie:
a) wyznaczaliśmy rezystancję wewnętrzną galwanometru metodą jednakowych odchyleń. Analizując otrzymany wynik możemy powiedzieć, że uzyskana wartość Rg jest zbliżona do wartości podanej na tabliczce znamionowej, jednak różnica jest znaczna(117Ω), powodem tego może być zmiana właściwości galwanometru wraz z wiekiem urządzenia
W punkcie:
b) wyznaczona wartość rezystancji krytycznej mieści się w granicy podanej na galwanometrze.
W punkcie:
c) wyznaczaliśmy stałą prądową galwanometru, wynik z doświadczenia mieści się w granicy i jest bliższa górnej wartości znamionowej. Okresu wahań nie tłumionych T0 nie wyznaczyliśmy z powodu braku czasu.
W2
RD
RN
R2
W1
E
R1
P
mA
G
Wyszukiwarka
Podobne podstrony:
Metrologia 7(1), Politechnika Lubelska, Studia, semestr 5, Sem V, Nowy folder
Metrologia 1, Politechnika Lubelska, Studia, semestr 5, Sem V, Nowy folder
Metrologia 3, Politechnika Lubelska, Studia, semestr 5, Sem V, Nowy folder
Metrologia 4(1), Politechnika Lubelska, Studia, semestr 5, Sem V, Nowy folder
Metrologia 2, Politechnika Lubelska, Studia, semestr 5, Sem V, Nowy folder
Metrologia 5, Politechnika Lubelska, Studia, semestr 5, Sem V, Nowy folder
Metrologia 23 protokół, Politechnika Lubelska, Studia, semestr 5, Sem V, Nowy folder
Metrologia 18, Politechnika Lubelska, Studia, semestr 5, Sem V, Nowy folder
Metrologia 16, Politechnika Lubelska, Studia, semestr 5, Sem V, Nowy folder
Metrologia 16 protokół, Politechnika Lubelska, Studia, semestr 5, Sem V, Nowy folder
Metrologia 10(1), Politechnika Lubelska, Studia, semestr 5, Sem V, Nowy folder
Metrologia 25, Politechnika Lubelska, Studia, semestr 5, Sem V, Nowy folder
Metrologia 26 protokół, Politechnika Lubelska, Studia, semestr 5, Sem V, Nowy folder
Metrologia 10 protokół, Politechnika Lubelska, Studia, semestr 5, Sem V, Nowy folder
Metrologia 20 protokół, Politechnika Lubelska, Studia, semestr 5, Sem V, Nowy folder
Metrologia 4. protokół, Politechnika Lubelska, Studia, semestr 5, Sem V, Nowy folder
Metrologia 2 protokół, Politechnika Lubelska, Studia, semestr 5, Sem V, Nowy folder
Metrologia 11 protokół, Politechnika Lubelska, Studia, semestr 5, Sem V, Nowy folder
więcej podobnych podstron