transformacja

1. Transformacja pierwiastkowa - tę już wyżej objaśniliśmy. Kiedy się nią posłużyć? Jedna tylko uwaga techniczna, gdy w zbiorze danych występują wyniki mniejsze od 10, to wówczas posłużymy się nieco zmodyfikowanym wzorem:

Y'_k =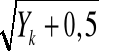
. Stosujemy ją, gdy rozkład Y jest rozkładem Poissona, jaki ma np. liczba błędów popełnianych przez osoby badane w trakcie rozwiązywania jakiegoś zadania. Stosujemy je także wtedy, gdy wariancje w grupach porównawczych są proporcjonalne do średnich grupowych - gdy między s²_i i Y_i zachodzi, rzecz jasna, że w przybliżeniu, zależność liniowa.

2. Transformacja logarytmiczna:

Y'_k = log Y_k , a gdy wśród danych występują wyniki zerowe lub bardzo małe, to: Y'_k = log (Y_k + 1). Jest ona szczególnie przydatna, gdy wynikami są czasy reakcji (dość chętnie przez psychologów mierzone) i gdy ich rozkład jest wyraźnie dodatnio skośny. Posłużymy się nią, gdy wariancje są proporcjonalne do kwadratów średnich grupowych.

3. Transformacja ilorazowa:

Y'_k = 1/Y'_k , a gdy wśród danych występują wyniki zerowe, to stosujemy wzór:

Y'_k= 1/(Y_k + 1).

Znajduje ona zastosowanie, gdy zmienną zależną jest czas reakcji czy czas rozwiązywania problemów. Stosujemy przekształcenie ilorazowe, gdy odchylenia standardowe są proporcjonalne do kwadratów średnich.

D. Transformacja arcsin: Y' = 2arcsin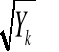
, gdzie Y wyrażony jest pod postacią proporcji.

W miejsce 0 i 1 wstawiamy, odpowiednio,

„1/4n” i „1 - 1/4n”

(n - liczba obserwacji).

Ta transformacja jest zalecana, gdy wyniki wyrażone są pod postacią proporcji, np. proporcja poprawnych odpowiedzi w jakimś teście.

2