LAB 1
1. Szereg statystyczny - otrzymujemy wówczas, kiedy dane statystyczne zostaną sklasyfikowane wg jakiegoś kryterium.
Szereg szczegółowy - najczęściej stosowany jest w przypadku, gdy liczba jednostek objętych badaniem jest na tyle mała, że czytelnym i rozsądnym jest uporządkować je kolejno.
Szereg rozdzielczy punktowy - buduje się zwykle gdy liczba wariantów danej cechy jest niewielka a każdy z tych wariantów występuje kilka razy.
Szereg rozdzielczy przedziałowy - powstaje w wyniku podziału zbiorowości na klasy i podanie liczebności klas.
2. Liczebność - określa ilość danych w danym zbiorze
Częstość - stosunek liczby obserwacji posiadających pewną właściwość do liczebności całej próby statystycznej.
B. Liczebność skumulowana, częstość skumulowana
Częstość skumulowana - nazywamy sumę częstości tej klasy i częstości klas poprzednich.
Suma liczebności przedziałów poprzedzających przedział mediany, czyli liczebność skumulowana.
Skumulowany wskaźnik struktury (inaczej: częstość skumulowana)
gdzie nisk oznacza liczbę jednostek, których cechy odpowiadają wartościom nie większym niż xi.
3. Przedstawić sposób obliczania średniej arytmetycznej, eksperymentalnej wariancji (estymator nieobciążony) i odchylenia standardowego na podstawie n niepogrupowanych danych x1, x2, xn.
Średnia arytmetyczna i eksperymentalne odchylenie standardowe:
xi- warianty cechy zmiennej,
n- liczebność zbioru.
Eksperymentalna wariancja:
xi- warianty cechy zmiennej (wyniki pomiarów)
n- liczebność zbiorowości,
u- wartość oczekiwana,
~x- średnia arytmetyczna.
4. Podać definicje mediany, modalnej, kwartyli (pierwszy i trzeci)
Mediana (zwana też wartością środkową lub drugim kwartylem) to w statystyce wartość cechy w szeregu uporządkowanym, powyżej i poniżej której znajduje się jednakowa liczba obserwacji. Mediana jest kwantylem rzędu 1/2, czyli drugim kwartylem
Dominanta (wartość modalna, moda, wartość najczęstsza) jedna z miar tendencji centralnej, statystyka dla zmiennych o rozkładzie dyskretnym, wskazująca na wartość o największym prawdopodobieństwie wystąpienia, lub wartość najczęściej występująca w próbie.
Kwartyl - kwantyl rzędu 1/4 (pierwszy kwartyl, dolny kwartyl), 1/2 (mediana) lub 3/4 (trzeci kwartyl, górny kwartyl).
Mediana - kwartyl drugi - dzieli zbiorowość na dwie równe części; połowa jednostek ma
wartości cechy mniejsze lub równe medianie, a połowa wartości cechy równe lub większe od Me; stąd nazwa wartość środkowa
Modalna - jest to wartość cechy statystycznej, która w danym rozdziale empirycznym występuje najczęściej.
Kwartyle - definiuje się jako wartości cechy badanej zbiorowości, przedstawionej w postaci
szeregu statystycznego, które dzielą zbiorowość na określone części pod względem liczby
jednostek, części te pozostają do siebie w określonych proporcjach.
Kwartyl pierwszy Q1 - dzieli zbiorowość na dwie części w ten sposób, że 25% jednostek
zbiorowości ma wartości cechy niższe bądź równe kwartylowi pierwszemu Q1, a 75% równe bądź wyższe od tego kwartyla.
Kwartyl trzeci Q3 - dzieli zbiorowość na dwie części w ten sposób, że 75% jednostek zbiorowości ma wartości cechy niższe bądź równe kwartylowi pierwszemu Q3, a 25% równe bądź wyższe od tego kwartyla.
5. Jak określić modalną i medianę, dysponując danymi uporządkowanymi?
6. Jak oblicza się średnią arytmetyczną z szeregu rozdzielczego punktowego ?
xi- warianty cechy zmiennej,
ni (i=1,2,k)- liczebność cząstkowa (waga) danej cechy,
n- liczebność zbioru.
7. W jaki sposób można określić medianę na podstawie wykresu liczebności skumulowanej?
8. Wyjaśnić, kiedy należy stosować średnią harmoniczną i jak ją obliczać.
Średnią harmoniczną stosuje się w przypadku gdy wartości zmiennej podane są w jednostkach względnych (np. m/s, cm/osoba), natomiast wagi są w jednostkach liczników tych jednostek względnych (np. m, cm).
Średnią harmoniczną n liczb dodatnich
nazywamy liczbę:
9. Jak oblicza się odchylenie standardowe średniej?
10. W jaki sposób określa się niepewność standardową obliczaną metodą typu A dla pojedynczego wyniku pomiaru i dla średniej?
W metrologii odchylenie standardowe nazywane jest niepewnością standardową pojedynczego wyniki obliczaną metodą typu A i oznacza się jako uA(X):
uA(X) = s.
Gdy obliczana jest wartość średnia z wyników, to niepewność standardowa średniej obliczana metodą typu A jest równa odchyleniu standardowemu średniej S~x:
LAB 2
1. Wyjaśnić różnice pomiędzy zmienną losową ciągłą a dyskretną.
Jeżeli wartości zmiennej (cechy) są określone przez przypadek to mówimy, że zmienna ta jest
zmienną losową.
Zmienne losowe dzielimy na:
-ciągłe- zmienna przyjmuje dowolne wartości z określonego
przedziału (w szczególności cały zbiór liczb rzeczywistych)
zbiór wartości, które może przyjmować zmienna jest nieprzeliczalny.
-skokowe (dyskretne)- zmienna przyjmuje dowolne
wartości ze zbioru przeliczalnego lub skończonego (np. zbiór liczb całkowitych
z określonego przedziału)
Zmienną losową nazywamy skokową, jeżeli zbiór wartości, które może przyjmować zmienna jest skończony lub przeliczalny. Zmienną losową nazywamy ciągłą, jeżeli zbiór wartości, które może przyjmować zmienna jest nieprzeliczalny.
2. Omówić sposób wyznaczania histogramu na podstawie n wartości niepogrupowanych danych x1,x2,xn.
3. Jak określa się liczbę klas przy tworzeniu histogramu?
Obliczanie liczby klas histogramu ze wzoru Sturgesa:
k ≈ 1 + 3,322 log(n)
n - liczebność zbioru. Jest to wzór empiryczny stosowany dla dużej liczby wyników.
4. Wyjaśnić różnicę pomiędzy rozkładem gęstości prawdopodobieństwa a histogramem.
Funkcja gęstości prawdopodobieństwa ciągłej zmiennej losowej X to pewna funkcja f przyjmująca wartości wyłącznie nieujemne i taka, że
Histogram to jeden z graficznych sposobów przedstawiania rozkładu cechy. Składa się z szeregu prostokątów umieszczonych na osi współrzędnych.
Prostokąty te są z jednej strony wyznaczone przez przedziały klasowe (patrz: Szereg rozdzielczy) wartości cechy, natomiast ich wysokość jest określona przez liczebności (lub częstości) elementów wpadających do określonego przedziału klasowego.
5. Narysować funkcje prawdopodobieństwa i dystrybuantę zmiennej losowej, określonej na zbiorze zdarzeń elementarnych odpowiadających wynikom rzutu kostką.
6. Jakie parametry charakteryzują rozkład normalny i w jaki sposób wpływają one na przebieg funkcji gęstości prawdopodobieństwa oraz dystrybuantę tego rozkładu?
W przypadku rozkładu normalnego o funkcji gęstości danej wzorem:
Dla podanych niżej przedziałów wartości procentowe liczby wyników są następujące:
Dla μ±σ jest 68,27% co odpowiada Pr(σ<= μ<= σ)=0,6827,
dla μ±2σ jest 95,45% co odpowiada Pr(2σ<= μ<=2 σ)=0,9545,
Dla μ±3σ jest 99,73% co odpowiada Pr(3σ<= μ<= 3σ)=0,9973.
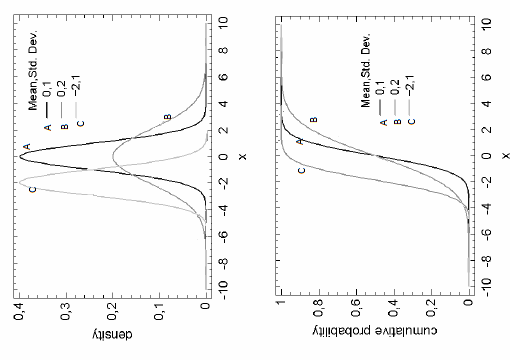
7. Narysować funkcje gęstości prawdopodobieństwa dla zmiennych losowych o rozkładach normalnych N(0,1), N(0,2), N(-2,1).
8. Narysować rozkład częstości (wielokąt częstości) i dystrybuantę empiryczną dla podanego w tabeli rozkładu punktów uzyskanych na egz. Określić, jaki procent studentów uzyskał co najmniej 20, ale mniej niż 40 punktów.
10. Podać sposób obliczania średniej arytmetycznej, wariancji i odchylenia standardowego populacji dla danych pogrupowanych w szereg rozdzielczy punktowy.
xi- warianty cechy zmiennej,
ni- liczebność cząstkowa danej cechy (klasy),
n- liczebność zbiorowości, k- liczba klas.
1
Wyszukiwarka
Podobne podstrony:
sciaga zarz dzanie zaliczenie www.przeklej.pl, Studia, Semestr 1, Zarządzanie
marketingowy system informacji www przeklej pl
phmetria www przeklej pl
inventor modelowanie zespolow www przeklej pl
prob wki www.przeklej.pl, Ratownictwo Medyczne
rozw j teorii literatury wyk zag do egz www przeklej pl
pytania www przeklej pl
hih wyniki kolokwium 21012010 www przeklej pl
referaty na materia oznawstwo www.przeklej.pl, Rok II, laborki z termy
micros atmel www przeklej pl
klucz do skutecznej komunikacji www przeklej pl
ex 2009 2 www przeklej pl
notatka utk www.przeklej.pl, ściągi
hdd www.przeklej.pl, ściągi
pg egz www przeklej pl
ergonomia www przeklej pl
pbigp moje www przeklej pl
więcej podobnych podstron