Podstawy Informatyki - 2. semestr studiów inżynierskich Energetyka

Program zajęć z podstaw programowania przy użyciu pakietu MATLAB

MATERIAŁY DLA STUDENTÓW

Prowadzący zajęcia: dr inż. Rafał Szłapczyński

Dane kontaktowe:

• Pok. 513

• Tel.: [phone]

• Email: [e-mail]

• Godziny konsultacji: 13.00-14.00.

Cel zajęć:

• Nabycie umiejętności projektowania algorytm*w

• Nauczenie się tworzenia oprogramowania oraz jego uruchamiania

• Nauczenie się prowadzenia podstawowych analiz przy pomocy utworzonych modeli

• Opanowanie podstaw pakietu MATLAB

Założenia:

• Program zajęć jest realizowany w ciągu 10 laboratoriów (3-godzinnych)

• Podstawą jest praca własna studenta nad problemami z podanego zestawu przykładowych zadań

• Opracowany zostanie projekt (do pokazania i przedyskutowania na ostatnim laboratorium)

Sposób prowadzenia zajęć

1. Studenci przygotowują się do laboratoriów samodzielnie, wg podanego zakresu zajęć:

1. Zobowiązani są do kompletnego rozwiązania samodzielnie zadań specjalnie wyszczególnionych przez prowadzącego.

2. Przygotowują algorytmy rozwiązań wszystkich przykładowych zadań z podanego wykazu zada* dla konkretnego laboratorium, co polega na posiadaniu pisemnych notatek zawierających algorytm i kod (bądź jego szkic).

2. W trakcie zajęć realizowane są zadania wybrane z podanego wykazu i studenci są oceniani za:

1. Gotowe rozwiązania zadań wyszczególnionych wcześniej przez prowadzącego

2. Realizowane na zajęciach pozostałe zadania z podanego wykazu

3. W trakcie zajęć przeprowadzone będą przynajmniej 3 sprawdziany, na zajęciach wyszczególnionych w planie.

Warunki zaliczenia

• Obecność i aktywna praca na laboratoriach. Pozytywne oceny z każdych zajęć.

• Pozytywne oceny ze sprawdzianów aplikowanych w trakcie zajęć

Uwagi dodatkowe dotyczące zaliczenia

• Ocena z MATLABA jest oceną składową oceny z przedmiotu.

• Studenci zobowiązani są do punktualności i dyscypliny na zajęciach.

• Każdy student zobowiązany jest do przynoszenia na zajęcia nośnika (dyskietka, pen-drive), w celu zarchiwizowania wyników swej pracy.

• Pytania i problemy studentów powinny być adresowane do prowadzącego, a nie do kolegów i koleżanek - głośne porozumiewanie się podczas zajęć utrudnia ich prowadzenie.

• Nieusprawiedliwione nieobecności skutkują obniżeniem oceny z przedmiotu.

• Trzy nieusprawiedliwione nieobecności automatycznie wykluczają zaliczenie i powodują skreślenie studenta z grupy laboratoryjnej

• W przypadku usprawiedliwionej nieobecności student jest zobowiązany do odrobienia jej lub samodzielnego nadrobienia zaległości i przygotowania się do następnych zajęć.

Absolutnie niezbędne wiadomości i umiejętności, które każdy student musi opanować:

• Podstawowe typy obiektów

• Operatory relacyjne, logiczne i arytmetyczne oraz ich stosowanie

• Instrukcja przypisania (podstawienia)

• Instrukcja if i else

• Instrukcja for

• Instrukcja while

• Instrukcja switch

• Tworzenie skryptów, ich nazewnictwo i uruchamianie

• Konstrukcja funkcji, jej parametry wejściowe i wyjściowe

• Stosowanie funkcji w skrypcie i środowisku interaktywnym MATLABA: wołanie z odpowiednimi parametrami i podstawianie wyniku do odpowiedniej zmiennej

Tematy realizowane w trakcie poszczególnych zajęć

LAB	Temat zajęć	Zakres
1	Podstawowe obiekty i operacje MATLAB-a. Skrypty - wstęp.	Poruszanie się w środowisku MATLAB: help, type, lookfor, path, cd, pwd, dir. Liczby. Łańcuchy. Skalary. Wektory. Macierze. Definiowanie tych obiekt*w. Operatory arytmetyczne. Operatory logiczne. Skrypty - wstęp
2-3	Skrypty. Podstawy konstrukcji algorytmu. Funkcje - podstawy	Użycie skrypt*w (m-plik*w skryptowych) dla wykonania sekwencji komend. Elementy języka: if, for, while i ich podstawowe użycie dla realizacji algorytmu. Konstrukcja funkcji. Parametry wejściowe i wyjściowe.
4	Sprawdzian 1. Podstawowe wykresy (1) - 2D	Sprawdzian 1. (LAB 1. i LAB 2.-3.) Funkcje wspomagające konstruowanie macierzy. Wykresy wizualizujące wektory i macierze. Plot. Subplot. Axis. Opis wykresu. Hold. Grid.
5	Macierze i ich przetwarzanie	Tworzenie macierzy: wyliczanie, generowanie element*w, budowanie z innych macierzy. Adresowanie element*w: pojedynczych, podmacierzy. Wektory zerojedynkowe i ich zastosowanie do wyboru element*w macierzy. Rozmiary macierzy. Operatory macierzowe: suma, różnica; mnożenie macierzy; transpozycja macierzy. Operacje odwracania macierzy. Dzielenie prawo, lewostronne, pseudoinverse. Potęgowanie macierzy. Rozwiązywanie układów równań liniowych.
6-7	Sprawdzian 2. Skrypty i Funkcje	Sprawdzian 2. (LAB 4. i LAB 5.) Wczytywanie danych z klawiatury. Konstrukcja złożonych algorytmów.
8	Wykresy (2) Użycie funkcji	Nierównomierne osie. Porównanie działanie różnych funkcji bibliotecznych służących do sporządzania wykresów. Histogram. Rose. Stem. Comet. Polar. Compass. Patch. Fill. Fplot.
9	Sprawdzian 3. Operacje I/O. Grafika 2D	Sprawdzian 3. (LAB 6., LAB 7., LAB 8) Zapis i odczyt zmiennych MATLABA. Kontrolowany zapis i odczyt plik*w. Interakcyjne wprowadzanie i wyprowadzanie danych (input, disp - w rozszerzonym zakresie - reakcje na błędy). Funkcje: Line i Fill
10	Grafika 3D. Powtórka i podsumowanie.	Sprawdzian 4. (LAB 1. - LAB 9., szczególnie LAB 8.) Przygotowanie danych dla formy wymaganej przez procedury grafiki 3D. Podstawowe typy wykres*w: kontury, siatki, powierzchnie. Modyfikacja podstawowych typów wykres*w: oświetlenie, mapy kolor*w. Ukryte linie i powierzchnie. Wizualizacja: view, viewmtx. Odbieranie prac domowych. Zaległe zaliczenia sprawdzianów. Podsumowanie. Wystawienie ocen.

Przykładowe zadania do zajęć z każdego z powyższych temat*w

Część podanych zadań zawiera wielkości, które powinny być zdefiniowane samodzielnie i przyjęte przez studenta wykonującego zadanie (np., wielkości parametrów liczbowych).

Na każdym z laboratoriów Lab.1-10 będą realizowane wybrane zadania (lub ich fragmenty) z podanego niżej zestawu.

Uwaga:

Należy zawsze naszkicować sobie algorytm rozwiązania zadania. Służy on do samokontroli poprawności planowanego rozwiązania oraz jest podstawą do generacji kodu programu MATLABa.

Szkic taki powinien zawierać - z różnym stopniem szczegółowości - następujące elementy:

1. schemat przepływu informacji i sterowania w programie

2. listę i postać danych wejściowych

3. listę i postać danych wyjściowych oraz skutków ubocznych programu

4. pseudokod programu (lista operacji, dane dla każdej z operacji, wyniki każdej z operacji)

5. listę funkcji i operatorów planowanych do użycia w programie,

Materiały pomocnicze

1. A. Zalewski, R. Cegieła: “MATLAB - obliczenia numeryczne i ich zastosowania”

2. J. Brz*zka, L. Dorobczyński: “Programowanie w MATLAB”

3. “The Student Edition of MATLAB-The Language of Technical Computing-Ver. 5.3”

Pozycje (1-3) dostępne są w czytelni WOiO oraz w Zakładzie Technik Informatycznych.

LAB 1. Podstawowe obiekty i operacje MATLAB-a. Skrypty (m-pliki skryptowe) - wstęp

0. Po konfiguracji systemu MATLAB, użyj poleceń:

a) help; help sin;

b) type sin; type humps;

c) pwd, cd

d) path, path( path, `f:\matlab')

Każde z poleceń wpisuj w linii komendy po zachęcie EDU>>, np.

EDU>> help [enter]

EDU>> help sin [enter]

Obserwuj skutki ich wykonania. Użyj też okna pomocy systemu MATLAB.

Dla zachowania przebiegu sesji (wykonania poniższych zadań) użyj polecenia:

EDU>> diary nazwa_pliku

Zapisze to przebieg sesji w pliku o nazwie nazwa_pliku.

1. Oblicz warto*ci wyrażeń (wpisywanych w linii poleceń; MATLAB jest tutaj używany jako kalkulator; zwracane wartości są przechowywane w wewnętrznej zmiennej ans):

a) 1 + 2*3 - 4/5

b) 2² + 3^1/3

c) [(2 + 3j)*(2 - 3j)]² / (2 + 3j); j jest jednostką urojoną (j = sqrt(-1))

d) ln(2^1/3_­ + 3^1/4 - 1)

e) e^ln(2+j) * e^pi

Przykład e) - na zajęciach, reszta - w domu.

2. Nadaj wartości podanych wyrażeń zmiennym {x, X, s, S} i sprawdź - wpisując nazwę zmiennej w linii poleceń, czy te wartości zostały rzeczywiście przypisane tym zmiennym.

a) x: (3² + 4²)^-1/2

b) X: 1/3 + 1/(3*5) + 1/(5*7)

c) s: `MATLAB'

Przykład c) - na zajęciach, reszta - w domu.

3. Zbuduj następujące zmienne wektorowe:

a) V1 = [ 1 2 3 4 5 ]; V11 = [ -1 -3 -5 ]

b) V2 = [ 6 7 8 9 10 ]; V22 = [ -11 -15 ]

Użyj następujących technik:

- przez wyliczenie wszystkich element*w wektora

- przez wygenerowanie element*w wektora przy pomocy wyrażenia:

nazwa_wektora = wartość_startowa : krok : wartość_końcowa

lub

nazwa_wektora = wartość_startowa : wartość_końcowa

4. Zbuduj zadane macierze (separatory: „ , ” , ” ; ”). Zadanie zrealizuj za pomoca skryptu.

Uwaga: wszystkie skrypty (m-pliki skryptowe) pisane w tym laboratorium powinny być umieszczone w roboczych katalogach studenta (np., w F:\matlab\lab2). W związku z tym należy umieścić te katalogi w ścieżce przeszukiwania MATLAB-a (polecenie path()). Warto również zmienić katalog do pożądanego katalogu roboczego (polecenia cd i pwd). Wszystkie te polecenia można umieścić w skrypcie startup.m znajdującym się w katalogu roboczym studenta, z którego uruchamiany jest MATLAB (zazwyczaj F:\matlab).

Skrypt (m-plik skryptowy) zawiera ciąg poleceń MATLAB-a. Po edycji skryptu przy pomocy edytora tekstu wbudowanego w system MATLAB można zachować ten skrypt na dysku (nazwa pliku powinna koniecznie mieć rozszerzenie .m, np. xxxx.m ). Wykonanie zapisanego w nim ciągu poleceń dokonuje się poprzez wpisanie nazwy skryptu w linii poleceń MATLAB-a ( EDU>> xxxx.m [enter] ).

a)

b)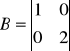
,

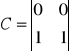
c)

d) macierz o wierszach będących łańcuchami:

`WOiO', `Grupa 1', Grupa 2', `ETI', `PG', `Gdynia' (możesz wyliczyć elementy lub użyć funkcji str2mat())

5. Sprawdź wyniki działania operator*w relacyjnych (<, <=, >, >=, ==, ~=) i logicznych (& - koniunkcja, | - alternatywa, ~ - negacja, xor() - różnica symetryczna) dla następujących obiekt*w (skalar*w, wektor*w i macierzy):

a) liczb 3 i 7

b) dla zmiennych skalarnych x = 0 i y = 2,1;

c) dla wektor*w X = [1 2 0] i Y = [1 0 3];

d) dla macierzy A = [0 1; 1 0] i B = [0 2; 0 1];

e) dla łańcuchów s1 = `abc' i s2 = `aBC';

6. Napisz skrypt (m-plik skryptowy), generujący następujące macierze:

a) macierz jednostkową A­_5x5 , używając funkcji eye()

b) macierz B_5x5 o wszystkich elementach równych 5, używając funkcji ones()

c) macierz C_5x2 wypełnioną zerami, używając funkcji zeros()

d) macierz D_10x10 wypełnioną liczbami losowymi, używając funkcji rand() lub randn()

e) przekształć macierz A w macierz E poleceniami rot90(), fliplr(), flipud()

Obejrzyj strukturę każdej z powyższych macierzy, używając funkcji spy(). Aby zatrzymać przewijanie ekranu wynik*w, użyj w skrypcie polecenia pause.

LAB 2.-3. Elementy języka (instrukcje: if, switch, for, while). Podstawy konstrukcji algorytmów. Wstęp do funkcji.

1. Napisz skrypt znajdujący największy element wektora liczb.

2. Napisz skrypt zamieniający miejscami dwa elementy wektora o zadanych indeksach.

3. Napisz skrypt sortujący zadany wektor liczb.

4. Napisz skrypt sprawdzający, czy dana liczba jest liczbą pierwszą.

5. Napisz skrypt obliczający największy wspólny dzielnik dwóch liczb naturalnych.

6. Napisz skrypt obliczający najmniejszą wspólną wielokrotność dwóch liczb naturalnych.

7. Zamień napisane skrypty na funkcje o odpowiednich parametrach

LAB 4. Sprawdzian 1. Podstawowe wykresy (1) - 2D.

1. Napisz skrypt (m-plik skryptowy) wykreślający 3 następujące funkcje:

1. y = sin(x),

2. y = cos(x),

3. y = sin(2*x),

dla x z przedziału <-2*π,2*π>.

Musisz wygenerować wektor x (start:krok:koniec) oraz wektory odpowiadających mu wartości y(x) poszczególnych funkcji. Całe okno graficzne podziel na oddzielne wykresy (po jednym dla każdej z funkcji).

Sporządź wykres przy użyciu funkcji plot(), stem(), stairs() i bar()

Użyj funkcji subplot() do podzialu okna graficznego.

Opisz wykresy: wstaw tytuły oraz opisy osi (funkcje title(), xlabel(), ylabel() )

Przykład c) - na zajęciach, reszta - w domu.

2. Napisz skrypt wyszukujący elementy macierzy spełniające zadane kryterium i pokazujący lokalizację tych element*w.

a) utw*rz macierz A_20x20 o elementach będących liczbami pseudolosowymi o rozkładzie normalnym N(0,1) - użyj funkcji randn();

b) znajdź elementy macierzy A większe od zera (zastosuj operator relacyjny > ; wyniki wpisz do macierzy B) i pokaż ich lokalizację przy pomocy funkcji spy()

c) powt*rz tę operację (punkty a i b) - czy wykres wygląda inaczej ?

d) zmień warunek logiczny - szukaj element*w macierzy A większych kolejno od 1, od 2, od 3; pokaż lokalizację tych element*w

4. Napisz skrypt rysujący na jednym wykresie 3 następujące funkcje:

y = atan(x), y = humps(x), y = sin²(x)

Określ przedział, w którym maj* by* obliczane i rysowane powyższe funkcje. Utwórz wektor x oraz wektory y(x) wartości funkcji odpowiadających zmiennej x. Narysuj wykresy, dodaj*c do tego samego rysunku kolejne funkcje (musisz użyć polecenia hold ).

Lab 5. Macierze i ich przetwarzanie

1. Dane są macierze:

,

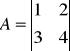
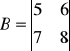
a) Utw*rz z podmacierzy A i B macierz C o strukturze

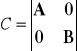
, sprawdź wynik przy pomocy funkcji spy()

2. Dopisz do macierzy C wiersz i kolumnę jedynek;

2. Nadaj elementom leżącym na gł*wnej przekątnej wartość 1 (uwaga: potraktuj macierz C jako wektor kolumnowy; skonstruuj wektor indeks*w dla wyboru element*w leżących na głównej przekątnej; wybierz przy jego pomocy te elementy i nadaj im wszystkim - jedną operacją - wartość 1);

3. Przestaw wszystkie kolumny macierzy C tak, by ostatnia kolumna była pierwszą (lustrzane odbicie lewo-prawo macierzy wejściowej); powt*rz to samo z wierszami (lustrzane odbicie g*ra-d*ł macierzy wejściowej); użyj do tego wektor*w indeks*w r; chodzi o operację typu: x = y( n:-1:1 ; : ) ;

4. Usuń z macierzy C ostatni wiersz i ostatnią kolumnę (użyj macierzy pustej [] i odpowiedniego indeksowania)

2. Używając funkcji diag() i ones(), utw*rz macierz trójdiagonalną D_5x5, kt*ra na gł*wnej przekątnej ma elementy r*wne 4, zaś na przekątnych ponad oraz poniżej gł*wnej przekątnej ma elementy równe 1.

1. Zastąp wszystkie elementy r*wne (1) elementami r*wnymi (-1). Użyj do tego funkcji find(), size() i ones().

2. Wybierz z D podmacierz E_3x4 .

3. Wybierz z D podmacierz F_3x5, która składa się z 1,3 i 5 wiersza macierzy D

3. Stabelaryzuj poniższe funkcje (wygeneruj wektor zmiennej niezależnej x oraz odpowiadający mu wektor warto*ci funkcji y(x)). Dobierz samodzielnie zakres zmiennej x oraz krok tabelaryzacji.

1. 
   

2. 
   

4. Utwórz wektory A = [1 2 3 4] oraz B = [5 6 7 8].

1. dodaj A i B; od A odejmij B;

2. do A dodaj -1; pomnóż B przez 2;

3. pomnóż skalarnie A*B

4. pomnóż macierzowo A i B

5. pomnóż każdy element A przez odpowiadający mu element B

6. utwórz produkt tensorowy wektor*w A' i B, używając funkcji kron() (powinieneś otrzymać macierz K_4x4)

Uwaga: będziesz musiał użyć czasem operatora transpozycji `; dla sprawdzenia, czy operacje są dozwolone użyj funkcji size() (zwracającą wymiary macierzy)

5. Wygeneruj dwie prostokątne macierze A i B.

1. Pomnóż przez siebie macierze A i B (A*B)

2. Czy możliwa jest operacja B*A ?

3. Je*li b) jest możliwa, to czy A*B=B*A ?

6. Utw*rz dwie macierze kwadratowe C i D o tych samych wymiarach. Sprawdź, że:

1. det(C*D) = det(C)*det(D)

2. (C*D)^T = D^T*C^T

3. I*C = C*I; I jest macierzą jednostkową

Użyj funkcji eye() i det().

7. Rozwiąż następujący układ równań:

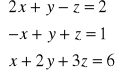
Napisz powyższy układ w dwóch postaciach macierzowych. Napisz rozwiązania symboliczne dla każdej z tych postaci.

Następnie rozwiąż numerycznie powyższy układ równań:

1. użyj do rozwiązania funkcji inv()

2. użyj operatora lewostronnego \ lub prawostronnego / dzielenia

Sprawdź otrzymane rozwiązania, wykonując odpowiednie mnożenia macierzowe.

8. Z pomiarów zarejestrowano zależność funkcyjną z = f(x,y). Dysponując tabelą trójek (x,y,z)_i określ współczynniki a,b,c liniowej funkcji Z = ax+by+c, przybliżającej zmierzone dane z=f(x,y).

X	1	2	3	4	5	6
Y	1	1	2	3	4	5
Z	4	6	9	12	15	20

Uwaga: sformułuj macierzowy układ równań; będzie to nadokreślony układ równań (więcej równań niż niewiadomych). Jeśli równania nie są zależne (czyli, gdy nie można odrzucić “nadmiarowych” równań, nie wnoszących nowej informacji), to nie możemy rozwiązać takiego układu “dokładnie”, natomiast można znaleźć jego rozwiązanie przybliżone, np. w sensie najmniejszych kwadrat*w. Operatory prawo- (/) i lewostronnego (\) dzielenia znajdują rozwiązania układ*w równań liniowych również w sensie najmniejszych kwadrat*w (czy najmniejszej normy). Znajdź współczynniki a,b,c. Oblicz wektor różnic r wartości funkcji z i jej przybliżenia Z: r = z - Z. Narysuj ten wektor różnic r.

Lab 6.-7. Sprawdzian 2. Skrypty i Funkcje. Wykresy(2).

1. Zaprogramuj zadane funkcje y(x) (napisz odpowiednie m-pliki funkcyjne), stablicuj te funkcje i sporządź wykresy tych funkcji. Dobierz samodzielnie kilka wartości parametru a funkcji y(x) oraz zakresy zmienności zmiennej niezależnej x.

a)

b)

Uwaga: wejściowy parametr funkcji (x) może być wektorem, więc programowane funkcje muszą używać wyrażeń uwzględniających ten fakt. M-pliki funkcyjne, definiujące funkcje y(x), nie powinny rysować wykres*w funkcji - powinny jedynie oblicza* wartości funkcji dla określonego zbioru warto*ci x i parametru a. Definiowanie parametr*w a, wektor*w x, tablicowanie warto*ci funkcji y(x), sporządzanie wykres*w powinno być dokonywane albo w oddzielnej funkcji, albo w skrypcie.

2. Zaprogramuj funkcję y(x) (napisz m-plik funkcyjny), określoną wzorem danym dla skalarnej warto*ci x:

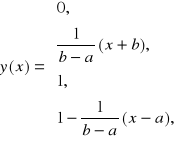
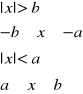
Podczas wywoływania (użycia) funkcji y(x) wartość x może być skalarem lub wektorem, więc funkcja powinna zwracać y(x) będące odpowiednio skalarem albo wektorem

Narysuj wykres tej funkcji w wybranym przez siebie przedziale zmiennej x. Uwaga: m-plik funkcyjny, definiujący y(x) nie może rysować wykresu tej funkcji (bo spowoduje to rekursję i w rezultacie błąd ochrony systemu WINDOWS).

3. Dane pomiarowe umieszczone są w kolumnach prostokątnej macierzy A_wxk. Dane dla jednego kanału pomiarowego są zapisane w j-tej kolumnie macierzy A (w danych), zaś dane dla pojedynczego pomiaru na wszystkich kanałach są zapisane w i-tym wierszu macierzy A (k danych).

1. wygeneruj testową macierz A_200x5, zawierającą dane testowe (dobrane samodzielnie);

2. oblicz średnią i wariancję danych dla każdego kanału pomiarowego;

3. wykreśl dane pomiarowe dla wybranych kanał*w; zaznacz średnią i odchylenie standardowe dla każdego kanału pomiarowego;

4. powtórz to wszystko dla macierzy B_500x3

Należy napisać odpowiednie funkcje (m-pliki funkcyjne), realizujące każdą z powyższych operacji. Cały program - czyli wszystkie operacje - może być skryptem.

4. Wygeneruj elementy a­_n ci*g*w liczbowych, których indeksy n (warto*ci zmiennej niezależnej n) dane są w wektorze inx (np, inx = [2 7 8] oznacza, że mamy wygenerować elementy a₂, a₇ i a₈). Narysuj wykresy wygenerowanych ciąg*w, czyli funkcji a_n(inx).

Wyrazy a_n rozważanych ciąg*w dane są następującymi wzorami:

a) a_n = a₁ + (n-1)r

b) a_n = a₁q^n-1

c) a_n = 2ⁿ/(n+2)!

d) a_n = (n+4)²/[2n⁴ + (n+4)²]

5. Napisz programy (m-pliki skryptowe lub m-pliki funkcyjne), obliczające całki oznaczone poniższych funkcji f w zadanych przedziałach. Użyj funkcji quad() oraz quad8(). Użyj opcji śledzenia obliczania funkcji podcałkowej (parametr TRACE ~= 0), by zobaczyć na wykresach, ile wartości funkcji podcałkowej f wymaga każda z tych procedur ca*kowania dla obliczenia zadanych całek oznaczonych.

1. f ≡ sin(x); x ∈< 0, π> (funkcja wewnętrzna MATLAB-a)

2. f ≡ humps(x); x ∈<0, π> (funkcja biblioteczna MATLAB-a)

3. f ≡ 1/(1+x²); x ∈<-10,10> (należy napisać tę funkcję jako m-plik funkcyjny)

Uwaga: nazwę konkretnej funkcji podcałkowej f należy przekazywać do funkcji quad() lub quad8() w postaci łańcucha (stałej łańcuchowej) lub zmiennej łańcuchowej.

6. Napisz program, który pozwala wykreślić funkcję jednej zmiennej, wpisaną przez użytkownika z klawiatury (w składni MATLAB-a). Przedział, w kt*rym funkcja ma być wykreślona, ma być też wpisany przez użytkownika z klawiatury. Będziesz musiał użyć następujących funkcji: input(), disp(), eval() i plot().

Np., użytkownik chciałby wpisać fragmenty dw*ch poniższych wierszy:

Przedział: 10:0.1:20

Funkcja f(t): sin(t).*exp(-t/5)

zaś napisany program powinien wykonać niezbędne obliczenia i wykreślić funkcję f(t) w przedziale zadanym przez użytkownika

7. Napisz program, kt*ry oblicza sumę S_k kolejnych k wyraz*w ciągu a_n . Sumowanie ulega zakończeniu, gdy |a_k+1| < e, gdzie e jest zadawane przez użytkownika. Powinna być zwrócona wartość S_k oraz ilość wyraz*w ciągu k, kt*re weszły w skład sumy S_k. Będziesz musiał użyć funkcji feval(). Oblicz sumy S_k dla podanych ciągów liczbowych i przy różnych wartościach e.

1. a_n = 0.8ⁿ;

2. a_n = 2ⁿ/(n+2)!; uwaga: musisz samodzielnie napisać funkcję silnia(n) lub skorzystać z zależności: silnia(n) = gamma(n+1) lub silnia(n) = exp(lngamma(n+1))

3. a_n = n!/(2^n!)

4. a_n = (-1)^(n-1) * x^(2n-1)/(2n-1)! ; x jest ustalone (np., 1); s* to kolejne wyrazy rozwinięcia w szereg Taylora funkcji sin(x)

8. Wykreśl krzywe całkowe poniższych funkcji F(x), będących funkcjami górnej granicy całkowania. Sprawdź przy pomocy wykres*w zależność każdej z tych funkcji od parametr*w odpowiednich funkcji podcałkowych f(x). Zadanie to może być rozwiązane za pomocą funkcji quad(). Funkcja górnej granicy całkowania F(x) dana jest wyrażeniem:

1. f(x) = e^-ax * sin(bx); x ∈<0, 2*π>; a,b > 0

2. f(x) = a/(1 + bx²); x ∈<0, 10>; a,b > 0

3. f(x) = a*e^-b*t*t; x ∈<0, 5>; a,b > 0

9. Napisz program obliczający numerycznie całkę oznaczoną funkcji wprowadzonej przez użytkownika z klawiatury dla przedziału również podanego z klawiatury. Zadanie należy rozwiązać bez korzystania z funkcji bibliotecznych quad() i ode23().

Lab 8. Wykresy (3) - użycie funkcji

1. Dane eksperymentalne podane s* w postaci par liczb (x,y)_i. Przedstaw te dane na wykresach o osiach różnego typu (logarytmicznych, równomiernych), tak, aby można było odgadnąć charakter funkcji y(x). Możesz użyć wykres*w semilogx(), semilogy(), loglog(), plot(). W oparciu o te wykresy przekształć wektory x i y tak, by przy użyciu funkcji plot() można było znaleźć parametry zależności funkcyjnej y(x).

a)

x	1	2	3	4	5	6	7	8	9	10
y	1.0000	2.3863	3.1972	3.7726	4.2189	4.5835	4.8918	5.1589	5.3944	5.6052

b)

x	1	2	3	4	5	6	7	8	9	10
y	2.7456	2.7732	2.8011	2.8292	2.8577	2.8864	2.9154	2.9447	2.9743	3.0042

c)

x	1	2	3	4	5	6	7	8	9	10
y	2	16	54	128	250	432	686	1024	1458	2000

2. Narysuj histogramy rozkład*w różnych zmiennych losowych X. Użyj funkcji hist() lub bar(). Po normalizacji histogramu (podzieleniu liczby warto*ci n_k występujących w poszczególnych podprzedziałach Δx_k zbioru warto*ci X przez iloczyn całkowitej liczby N losowanych wartości zmiennej losowych i długości podprzedziału Δx_k) otrzyma się przybliżenie funkcji gęstości prawdopodobieństwa p(X∈ Δx_k) = n_k./ (N*Δx_k). Sumując wartości przybliżonych prawdopodobieństw p(X∈ Δx_k) w kolejnych podprzedziałach histogramu uzyska się przybliżoną dystrybuantę rozkładu (całkę z funkcji gęstości prawdopodobieństwa), tj. wartość prawdopodobieństwa F zdarzenia, że X ma warto** mniejszą od x_k , [F(X < x_k)]. Narysuj na tym samym wykresie przybliżone funkcje gęstości rozkładu prawdopodobieństwa p oraz ich przybliżone dystrybuanty F.

1. zmienna losowa X o rozkładzie jednostajnym w przedziale <0,1> (funkcja rand())

2. zmienna losowa X o rozkładzie normalnym N(0,1) o średniej 0 i wariancji 1 (funkcja randn())

3. zmienna losowa X o rozkładzie jednostajnym w przedziale <a,b>; użyj wzoru:

gdzie R jest zmienną losową o rozkładzie jednostajnym w przedziale <0,1>

d) zmienna losowa X o rozkładzie normalnym N(m, var), tj. o średniej m i wariancji var; użyj wzoru:

gdzie N(0,1) jest zmienną losową o rozkładzie normalnym ze średnią 0 i wariancją 1

e) zmienna losowa X o rozkładzie wykładniczym o parametrze λ; użyj wzoru:

gdzie R jest zmienną losową o rozkładzie jednostajnym w przedziale <0,1>

3. Wykreśl przebieg wielomianu y(x) = x⁵ -3x³ + 1. Znajdź rzeczywiste miejsca zerowe tego wielomianu używając funkcji fzero(). Znajdź wszystkie pierwiastki wielomianu (rzeczywiste i zespolone) używając funkcji roots(). Sprawdź, czy są to naprawdę pierwiastki podanego wielomianu (oblicz wartości wielomianu w tych punktach przy pomocy funkcji polyval()). Wykreśl położenie pierwiastków na płaszczyźnie zespolonej używając funkcji compass() i plot().

4. Porównaj funkcje graficzne plot() i fplot(), używane do rysowania wykres*w funkcji. Dla porównania tych funkcji graficznych użyj następujących funkcji y(x):

1. 
   

2. 
   

Uwaga: wykresy sporządzone każdą z funkcji graficznych umieść w oddzielnym oknie (funkcja subplot()).

Lab 9. Sprawdzian 3. Operacje I/O

1. Napisz skrypt (m-plik skryptowy), kt*ry pozwoli sprawdzi* działanie operacji save i load.

1. utwórz kilka zmiennych; sprawdź ich istnienie poleceniem whos;

2. zapisz obszar roboczy (workspace) do pliku matlab.mat operacją save

3. usuń zmienne z obszaru roboczego operacją clear

4. sprawdź, czy zmienne istnieją nadal w przestrzeni roboczej poleceniem whos

5. załaduj zmienne z pliku matlab.mat do przestrzeni roboczej poleceniem load; sprawdź czy po tej operacji zmienne istniej* w przestrzeni roboczej

6. zapisz każdą ze zmiennych do oddzielnego pliku sekwencją poleceń save: w postaci binarnej i w postaci znakowej (ASCII); spróbuj obejrzeć zawartość tych plik*w przy pomocy polecenia VIEW (F3) w NortonCommander (nc)

7. usuń zmienne z obszaru roboczego; załaduj zmienne z oddzielnych plik*w; sprawdź, czy zmienne istnieją w przestrzeni roboczej;

2. W pliku znakowym (ASCII) zapisz dane o wielomianie: jego rząd i współczynniki. Napisz program, który:

1. oblicza wszystkie pierwiastki wielomianu i zapisuje raport o takich obliczeniach do pliku znakowego (powinny się tam znaleźć dane wejściowe oraz wyliczone pierwiastki);

2. tabelaryzuje wielomian w zadanym przedziale z zadanym krokiem tabeli, i zapisuje wyniki tych oblicze* do pliku znakowego (przedział tabelaryzacji i krok tabeli mogą znaleźć się w pliku danych lub mogą być podawane z klawiatury); przyjmij dane tak, by mieć nie więcej niż 30 punkt*w danych;

3. zagęszcza przedział zmiennej niezależnej tabeli (uzyskuj*c nowy wektor rzędnych xi) i interpoluje dane w tabeli, aby uzyskać interpolowane wartości wielomianu yi(xi); użyj funkcji interp1() i jej wszystkich trzech metod interpolacji; wyniki zapisz do pliku;

4. odczytaj pliki ze stabelaryzowaną funkcją (wielomianem) oraz z wynikami interpolacji; wykreśl te dane na jednym wykresie;

Uwaga: powinieneś użyć funkcji do formatowanego zapisu i odczytu plik*w (fopen(), fclose(), fscanf(), fprintf()).

3. W kryptografii często bada się częstość występowania poszczególnych znak*w w tekście. Napisz program, który:

1. czyta dowolny plik tekstowy - nazwę tego pliku podaje się z klawiatury (obsłuż ewentualne błędy);

2. określa częstości występowania poszczególnych znak*w w tekście;

3. rysuje wykres częstości występowania znak*w w przeczytanym tekście;

4. zapisuje raport o przeprowadzonej analizie do pliku;

Uwaga: prawdopodobnie będziesz musiał użyć* funkcji fgetl().

Uruchom swój program dla plik*w napisanych po polsku, po angielsku i dla plik*w z danymi numerycznymi.

4. Rozwinięcie programów z poprzednich laboratoriów o pobieranie danych z pliku i zapis wyników do pliku.

Lab. 10. Grafika 3D

1. Napisz programy, które przy pomocy funkcji comet3() i plot3() wizualizują następujące funkcje:

a)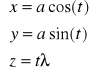
,
Przekazywane jako parametry użytkownika

b)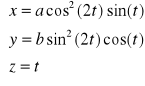
, a >0

2. Potencjał pola hydromechanicznego, które opisuje przepływ płaski wytwarzany przez źr*dło (upust) znajdujące się w punkcie (x_o,y_o), dany jest następującym wzorem:

, gdzie Q jest wydatkiem źródła (upustu)

Napisz program, który w zadanym obszarze prostokątnym przedstawia rozkład potencja*u φ wywołanego:

1. pojedynczym źródłem (upustem) o wydatku Q (-Q), umieszczonym w wybranym punkcie analizowanego obszaru płaszczyzny (x_o ,y_o);

2. źródłem i upustem o wydatkach Q i -Q, umieszczonych w różnych punktach (x_o1 ,y_o1) i (x_o2 , y_o2) analizowanego obszaru płaszczyzny (x,y); przeanalizować sytuację, gdy źr*dło i upust zbliżają się do siebie; wykorzystać addytywność potencjału, tj. Φ(X, (Q,P₁), (-Q,P₂)) = φ(X, Q, P₁) + φ(X, -Q, P₂)

Uwaga. Należy użyć następujących funkcji: meshgrid(), contour(), contour3(), mesh(), meshc(), surf(), surfc(). Jak wyglądają linie stałego potencja*u dla każdego z przypadków ?

3. Przeanalizować rozkład potencjału i gradientu potencjału (gradient potencjału to lokalna prędkość cieczy dla potencjału opisującego przepływ płynu) dla par potencjał*w opisujących przepływ płaski i przepływ przestrzenny. Analiza prowadzona jest na płaszczyźnie z=0. Użyj funkcji gradient() i funkcji graficznych wymienionych w zadaniu 2. Potencjały dane są następującymi wyrażeniami:

a) źr*dło:
, r² =(x-x_o)² + (y-y_o)²;
, r² =(x-x_o)² + (y-y_o)² + (z-z_o)²;

b) dipol umieszczony w początku układu współrzędnych:

, α jest kątem pomiędzy osią Ox a osią dipola

,

4. Napisz programy generujące bryły obrotowe. Wygeneruj wektory normalne do powierzchni tych brył. Zwizualizuj otrzymane powierzchnie i pola wektor*w normalnych.

1. hiperboloidę obrotową, o tworzącej generowanej równaniami
   

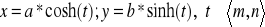
2. paraboloidę obrotową, o tworzącej opisanej w układzie biegunowym równaniem:
   

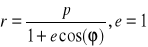
5. Napisz program pozwalający przeanalizować sposób, w jaki działają przekształcenia perspektywiczne. Przekształcenia perspektywiczne pozwalają przedstawić obiekty trójwymiarowe na dwuwymiarowym (płaskim) ekranie czy rysunku. Przekształcenie perspektywiczne realizowane jest przy pomocy funkcji viewmtx(), która zwraca 4x4 macierz transformacji (przekształcenia) T. Punkty obiektu są opisane poprzez zbiór współrzędnych uogólnionych (4 współrzędne dla jednego punktu) A. Stosując przekształcenie T do współrzędnych obiektu A uzyskujemy współrzędne po transformacji Y: Y = T*A. Pierwsze dwie kolumny (wiersze) macierzy Y są współrzędnymi x i y punktów w perspektywie, gotowymi do wykreślenia na płaszczyźnie ekranu.

Zdefiniuj jednostkowy sześcian. Przekształć sześcian używając transformacji perspektywicznych (viewmtx()). Wyniki przedstaw używając funkcji plot(). Porównaj z rysunkami uzyskanymi funkcją plot3().

6. Napisz program umożliwiający zbadanie różnego typu wykres*w trójwymiarowych (3D). Jako przykładowej funkcji dwóch zmiennych (x,y) użyj funkcji bibliotecznej peaks(). Prześledź efekt różnych funkcji (surf, surfl, mesh), różnych typ*w cieniowania (shading), różnego sposobu odbicia światła, różnych map kolor*w. Wykreśl paski kolor*w dla użytej mapy kolor*w, opisujących wartości funkcji peaks() przy pomocy różnych barw.

7. Napisz program, rysujący wszystkie standardowe mapy kolor*w MATLAB-a. Dołącz paski kolor*w, odwzorowujących zakres kolor*w na mapę kolor*w. Następnie, zmień zakres kolor*w (przy pomocy polecenia caxis()) i zobacz, jak wygląda mapa kolorów w przypadku rozszerzenia i zawężenia zakresu kolor*w. Zbuduj własną mapę kolor*w poprzez złożenie standardowych map kolor*w.

8. Napisz program, który ilustruje użycie standardowego, rozszerzonego i zawężonego zakresu kolor*w dla wizualizacji funkcji dwóch zmiennych. Jako przykładowej funkcji 2 zmiennych F(x,y) możesz użyć funkcji peaks() lub abs(peaks()). Narysuj wykresy 3D z paskami kolor*w oraz wykresy 2D z paskami kolor*w. Jako wykresy 2D proponuje się połączenie wykres*w uzyskanych przy pomocy funkcji pcolor() oraz contour(). (W domu)

Podstawy Informatyki - 2. semestr studi*w inżynierskich ENERGETYKA (2008): MATLAB

-Strona 1-

---