1

WYDZIAŁ TRANSPORTU PW Zakład Sterowania Ruchem

LABORATORIUM PODSTAW AUTOMATYKI III

Rok akad.

2015/2016

Data wykonania ćwiczenia

2015r.

Uzyskane

punkty

za:

Specjalizacja

Imiona i Nazwiska studentów

przygotowanie

i realizację

zaliczenie

poprawę

zaliczenia

. . . . . . . . . .

1.

Zespół

2.

3.

4.

5.

Ćwiczenie nr 1

Temat ćwiczenia: Badanie obiektów dynamicznych z zastosowaniem programu MATLAB

1

Cel ćwiczenia

Ćwiczenie ma na celu zapoznanie studentów z rozwiązywaniem problemów z zakresu automatyki z
użyciem programu MATLAB oraz Matlab Simulink.
Matlab to

program komputerowy będący interaktywnym środowiskiem do wykonywania

obliczeń naukowych i inżynierskich, oraz do tworzenia symulacji komputerowych.

Simulink jest częścią pakietu numerycznego MATLAB firmy The MathWorks i służy do
przeprowadzania symulacji komputerowych. Simulink pozwala budować modele symulacyjne przy
pomocy interfejsu graficznego i tzw. bloków. Przy pomocy Simulinka można przeprowadzać
zarówno symulacje z czasem dyskretnym jak i ciągłym. Simulink znajduje głównie zastosowanie
(poprzez to, że umożliwia symulacje w czasie ciągłym) w cyfrowym przetwarzaniu sygnałów,
analizie obwodów elektrycznych i teorii sterowania.

2

Niezbędny zakres tematyczny obowiązujący do przygotowania się do zajęć

Pojęcia: obiekt dynamiczny ciągły i liniowy, moduł transmitancji, kąt przesunięcia fazowego,
obserwowalność, sterowalność, stabilność (oraz kryteria i wyznaczanie obserwowalności,
sterowalności i stabilności – Nyquista, Bodego), układu dynamicznego i układu regulacji, równanie
charakterystyczne i wielomian charakterystyczny, stała czasowa w podstawowych członach
dynamicznych,
Charakterystyki układów dynamicznych – charakterystyki skokowe i częstotliwościowe,
interpretacja charakterystyk, sposoby wyznaczania charakterystyk, obliczanie modułu transmitancji
i przesunięcia fazowego.
Wyznaczanie zapasu stabilności.
Układy regulacji i parametry oceny regulacji.
Równania wektorowo-macierzowe układu dynamicznego. Macierze: stanu, wejścia i wyjścia.

3

Zasady współpracy z programem MATLAB

Wykonanie ćwiczenia należy rozpocząć od uruchomienia programu matlab - skrót na pulpicie.

Następnie za pomocą paska narzędzi wybrać File/Open/cw_automatyka.m, a następnie

zainicjowanie go przyciskiem run

. Po zainicjowaniu programu wyświetlone zostanie okno

dialogowe 'Matlab editor'. Należy wybrać opcję 'Change Folder'. Następnie uruchomiony zostanie
programu simulink, oraz okno nawigacyjne wykonane w interfejsie graficznym.

2

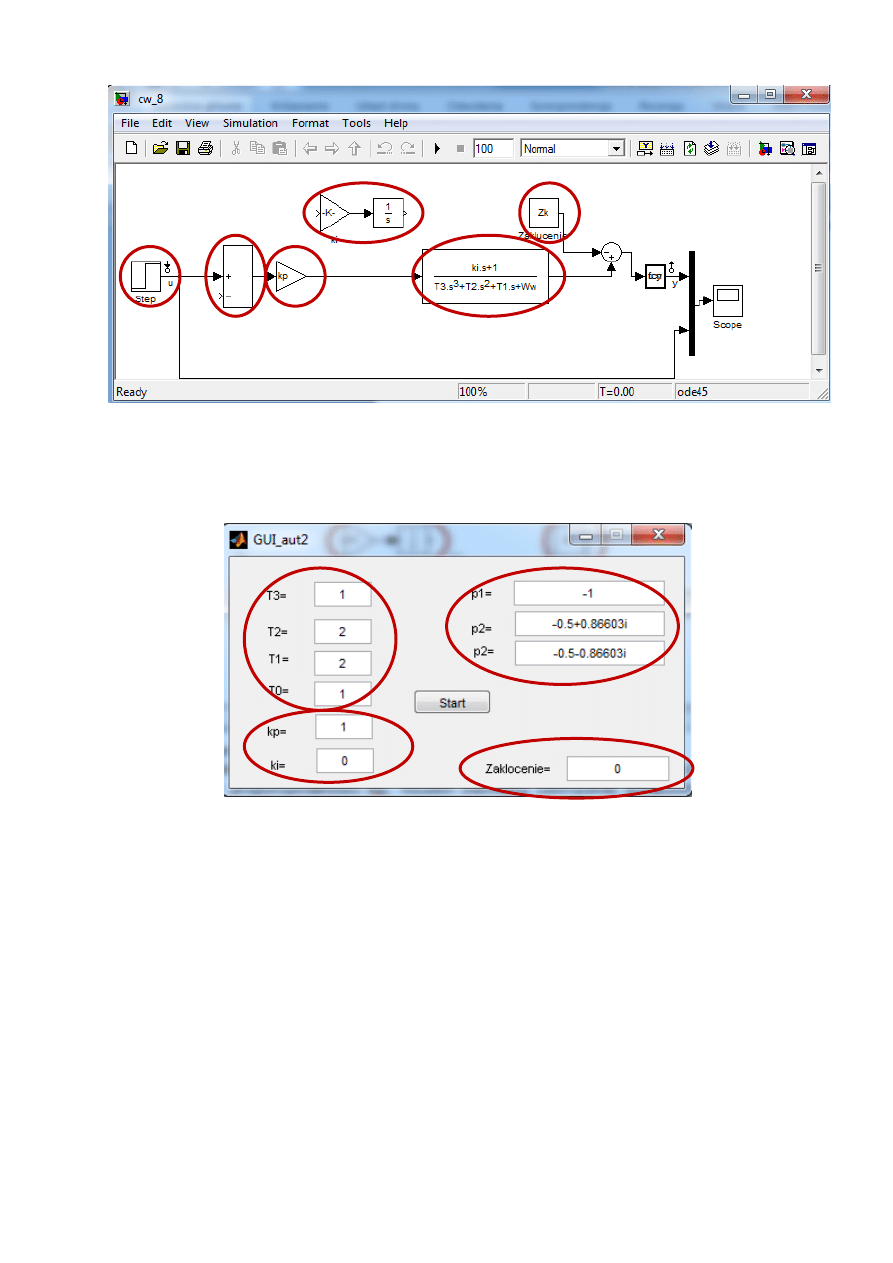
Rysunek 1Okno programu simulink
1)wymuszenie - skok jednostkowy, 2)węzeł sumujący (domyślnie bez sprzężenia zwrotnego),
3)współczynnik proporcjonalności kp, 4)człon inercyjny (domyślnie wyłączony), 5)obiekt n-tego
rządu (pierwszego, drugiego lub trzeciego), 6)zakłócenie

Rysunek 2 Okno interfejsu użytkownika
1) współczynniki wielomianu charakterystycznego, 2)współczynnik członu proporcjonalnego (kp) i
całkującego (ki), 3) pierwiastki wielomianu charakterystycznego, 4)zakłócenie (domyślnie zerowe)

4

Wykonanie ćwiczenia

4.1 Wyznaczenie charakterystyk skokowych.

Korzystając z interfejsu użytkownika wygenerować odpowiedź na skok jednostkowy obiektów

pierwszego, drugiego i trzeciego rzędu w otwartym układzie sterowania. Zidentyfikować wpływ
stałych czasowych oraz współczynnika proporcjonalności (kp). Zarejestrować przykładowe
charakterystyki, potrzebne do uzasadnienia działania współczynników.

1)

2)

3)

4)

5)

6)

1)

2)

3)

4)

3

4.2 Wyznaczenie charakterystyk amplitudowo-fazowych, kryterium Nyquista

Kryterium Nyquista pozwala na badanie stabilności jednowymiarowego układu zamkniętego na
podstawie przebiegu wykresu funkcji G ( jω) o układu otwartego na płaszczyźnie zmiennej
zespolonej.
Sformułowane przez Nyquista kryterium stabilności przedstawia się następująco:
1. Układ zamknięty jest stabilny asymptotycznie, przy założeniu, że równanie charakterystyczne
układu otwartego ma k pierwiastków w prawej półpłaszczyźnie i n-k pierwiastków w lewej
półpłaszczyźnie, wtedy i tylko wtedy, gdy charakterystyka amplitudowo-fazowa układu otwartego
przy zmianie pulsacji ω od -∞ do ∞ obejmuje w kierunku dodatnim k razy punkt (-1,j0)
2. Układ zamknięty jest stabilny asymptotycznie, przy założeniu, że równanie charakterystyczne
układu otwartego nie ma pierwiastków w prawej półpłaszczyźnie zmiennej zespolonej, wtedy i tylko
wtedy, gdy charakterystyka amplitudowo-fazowa układu otwartego przy zmianie pulsacji ω od -∞
do ∞ nie obejmuje punktu (-1,j0).
3. Na płaszczyźnie zmiennej zespolonej punkt (-1,j0) nazywamy punktem Nyquista.
W pewnych przypadkach wygodniej jest posługiwać tzw. regułą lewej strony, która mówi, że układ
zamknięty jest stabilny, jeżeli przy wzroście ω od 0 do ∞ , punkt (-1,j0) znajduje się w obszarze po
lewej stronie wykresu Go(jw).
W praktycznych zastosowaniach kryterium Nyquista jest szczególnie przydatne w przypadku, gdy
układ otwarty jest stabilny. Można wtedy korzystać z przebiegu charakterystyki G ( jω) o układu
otwartego zdjętej doświadczalnie, co pozwala na badanie stabilności także układu,
którego opis matematyczny nie jest znany.


Przyjmując wartości stałych czasowych zadanych przez prowadzącego zbadać stabilność obiektu
dynamicznego, korzystając z kryterium Nyquista.
Następnie sprawdzić odpowiedź obiektu dynamicznego w układzie zamkniętym.
Czy odpowiedź układu w układzie zamkniętym jest zgodna z oczekiwaniami?
Zarejestrować odpowiedź na skok jednostkowy, charakterystyki częstotliwościowe oraz pierwiastki
równania charakterystycznego układu otwartego i zamkniętego.

T0 T1

T2 T3

kp

ki

p1

p2

p3

Kryterium
stabilności
spełnione
(TAK/NIE)

0

0

0

4

4.3 Wyznaczenie zapasu stabilności

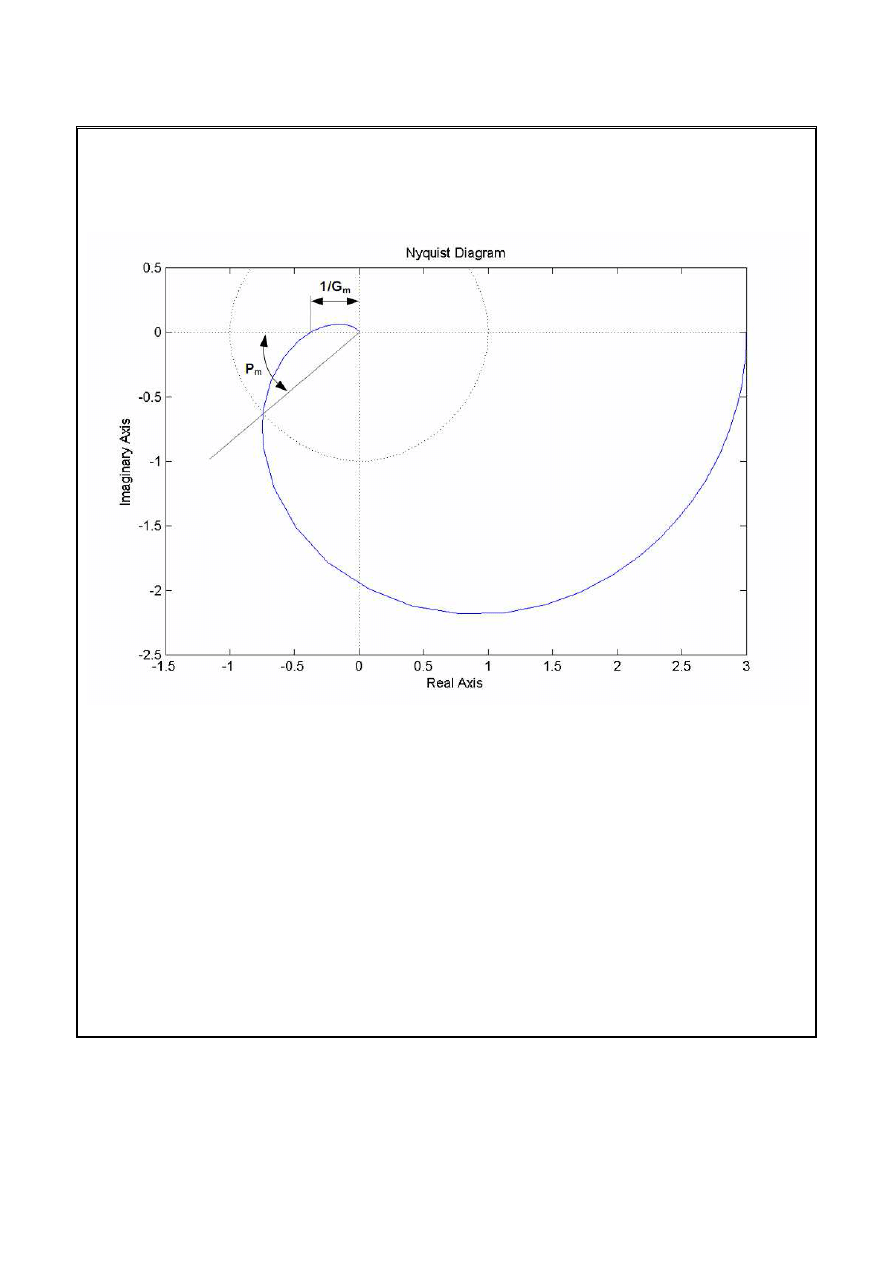
Zapas stabilności – Nyguist
Zapas wzmocnienia Gm – odwrotność długości odcinka wyznaczonego przez początek układu
współrzędnych oraz punkt przecięcia wykresu Nyquista z ujemną półosią Re(G(jω)).
Zapas fazy Pm – kąt między półprostą wychodzącą z początku układu współrzędnych i
przechodzącą przez punkt przecięcia wykresu Nyquista z kołem jednostkowym.

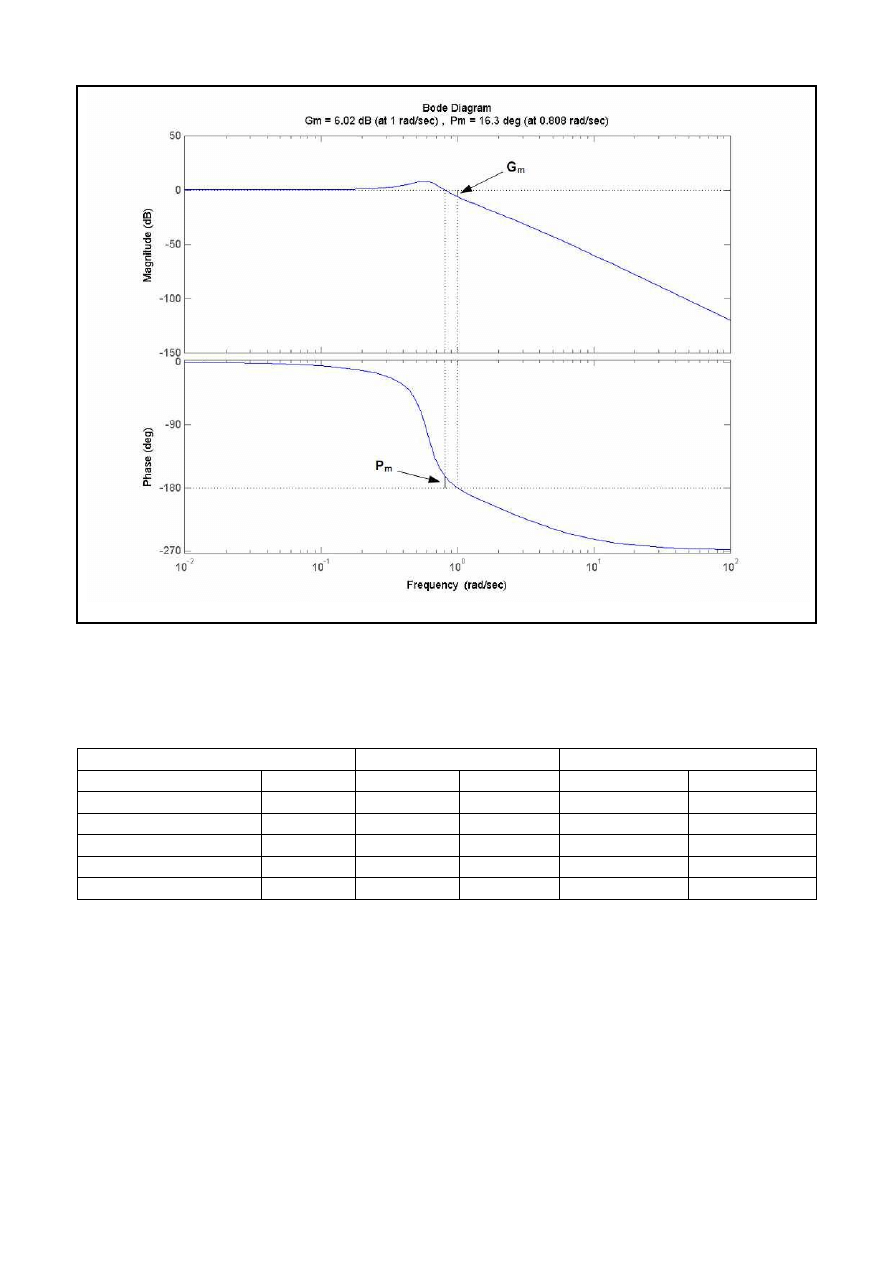
Wyznaczenie zapasu wzmocnienia i zapasu fazy na podstawie wykresów Bodego
Zapas wzmocnienia Gm (ang. gain margin) – wartość wzmocnienia, dla którego faza osiąga -
180°. Jego wartość oznacza o ile można zwiększyć wzmocnienie zanim stracimy stabilność.
Zapas fazy Pm (ang. phase margin) – wartość fazy dla częstotliwości, przy której wzmocnienie
wynosi 1 (0 dB). Jego wartość oznacza o ile można zmniejszyć przesunięcie fazowe zanim
stracimy stabilność.
W celu wyznaczenia zapasu fazy należy wyznaczyć tzw. pulsację odcięcia, tj. pulsacje ,która
spełnia warunek 20lg M(ωo)=0 a następnie określić fazę Φ(ωo). Zapasem fazy określa się
sumę _f= 180 - Φ(ωo) [deg] Jeśli jest ona dodatnia układ jest stabilny z zapasem fazy _f,
który mówi o tym, o ile można zwiększyć fazę układu otwartego bez zmiany jego
wzmocnienia, aby układ pozostawał jeszcze stabilnym . Zapas modułu można wyznaczyć
określając ω dla której Φ(ω -Π) = -180 deg a następnie pomierzyć dla tej samej pulsacji
moduł Lm(ω -Π) . Jest on równy zapasowi modułu, gdyż właśnie o tyle można zwiększyć
moduł w układzie, aby przy niezmiennej fazie pozostawał on stabilny. Aby wyznaczyć, o ile
można zwiększyć wzmocnienie układu otwartego, należy skorzystać z zależności: Lm=20lgK

5

4.3.1 Wyznaczenie zapasu stabilności w układzie zamkniętym z regulatorem proporcjonalnym
Wartości stałych czasowych przyjąć podane przez prowadzącego. Wartość współczynnika kp
dobrać tak aby układ był: stabilny, niestabilny, na granicy stabilności. Wyznaczyć zapas stabilności
korzystając z kryteriów Nyquista i Bodego. Zarejestrować otrzymane charakterystyki.
T0=...., T1=...., T2=..., T3=.....

Nyquist

Bode

kp

Gm

Pm

Gm

Pm

układ stabilny

układ stabilny

układ stabilny

układ niestabilny

układ na granicy stab.

Jaki jest wpływ współczynnika kp na zapas stabilności?
................................................................................................................................................................
................................................................................................................................................................
................................................................................................................................................................
................................................................................................................................................................
................................................................................................................................................................
...............................................................................................................................................................
................................................................................................................................................................

6

4.3.2 Wyznaczenie zapasu stabilności w układzie zamkniętym z regulatorem całkującym
Włączyć w układ szeregowo człon całkujący. Wartość kp ustawić na 1. Wartości stałych czasowych
przyjąć jak w poprzednim punkcie.
Wartość współczynnika ki dobrać tak aby układ był: stabilny, niestabilny, na granicy stabilności.
Wyznaczyć zapas stabilności korzystając z kryteriów Nyquista i Bodego.
Zarejestrować otrzymane charakterystyki.
T0=...., T1=...., T2=..., T3=.....

Nyquist

Bode

ki

Gm

Pm

Gm

Pm

układ stabilny

układ stabilny

układ stabilny

układ niestabilny

układ na granicy stab.

Jaki jest wpływ współczynnika kp na zapas stabilności?
................................................................................................................................................................
................................................................................................................................................................
................................................................................................................................................................
................................................................................................................................................................
................................................................................................................................................................
...............................................................................................................................................................
................................................................................................................................................................
4.3.3 Wyznaczenie zapasu stabilności w układzie zamkniętym z regulatorem proporcjonalnym
i całkującym
Wartości stałych czasowych przyjąć jak w poprzednim punkcie.
Wartość współczynników kp oraz ki dobrać tak aby układ był: stabilny, niestabilny, na granicy
stabilności. Wyznaczyć zapas stabilności korzystając z kryteriów Nyquista i Bodego.
Zarejestrować otrzymane charakterystyki.
T0=...., T1=...., T2=..., T3=.....

Nyquist

Bode

kp

ki

Gm

Pm

Gm

Pm

układ stabilny

układ stabilny

układ stabilny

układ niestabilny

układ na granicy
stab.

Jaki jest wpływ współczynników ki oraz kp na zapas stabilności?
................................................................................................................................................................
................................................................................................................................................................
................................................................................................................................................................
................................................................................................................................................................
................................................................................................................................................................
...............................................................................................................................................................
................................................................................................................................................................

7

4.4 Regulacja układu członem proporcjonalnym

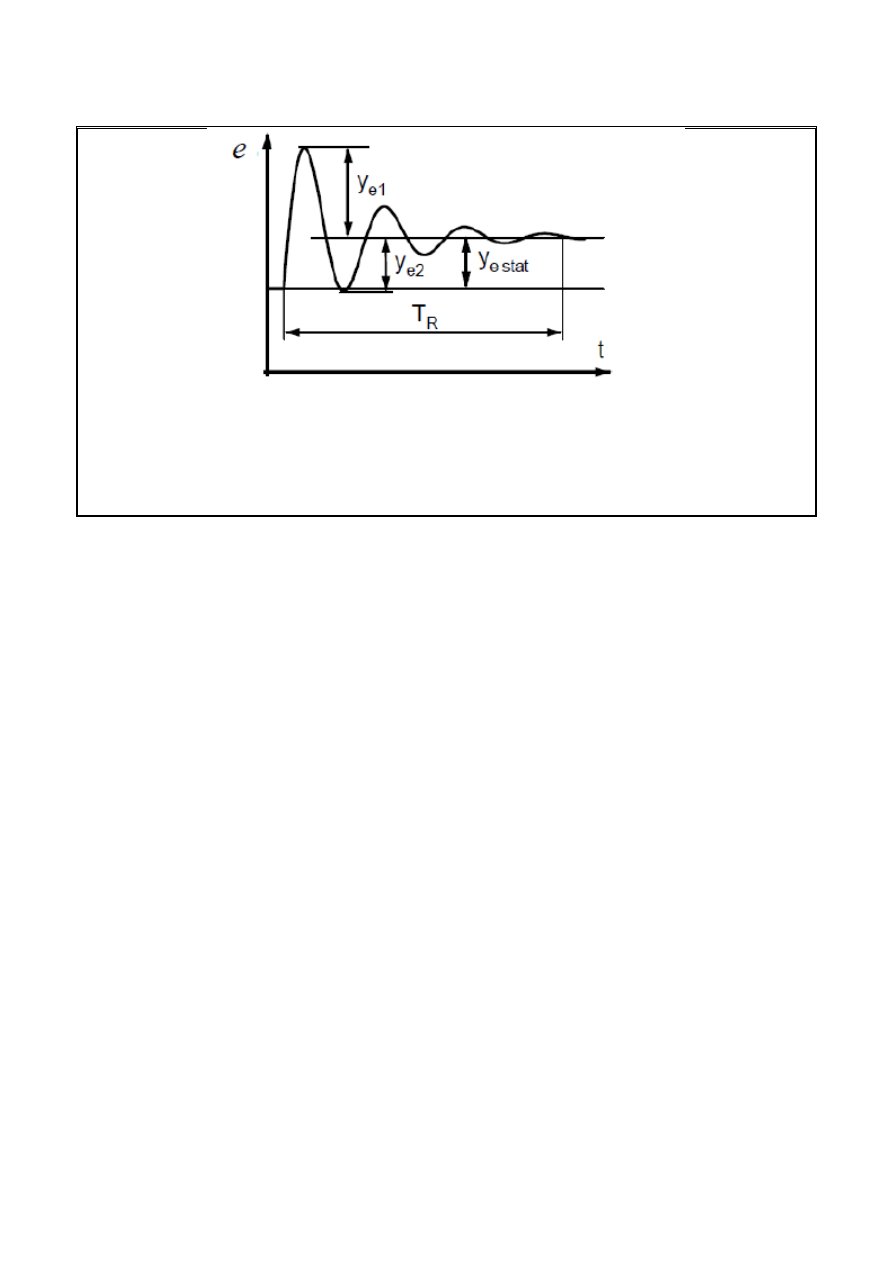
uchyb statyczny (ustalony)- w układzie regulacji jest to różnica między wartością zadaną sygnału
oraz wartością sygnału wyjściowego w stanie ustalonym.
czas regulacji - czas od chwili - czas o chwili pobudzenia do chwili gdy uchyb przejściowy zmaleje
trwale poniżej 5% wartości maksymalnej
przeregulowanie - jest stosunkiem początkowej maksymalnej wartości uchybu przejściowego do
największej wartości uchybu o znaku przeciwnym (y

e2

/y

e1

*100%)

Z układu wyłączyć człon całkujący. Wartość ki ustawić na 0.
W polu 'zakłócenia' wprowadzić wartość 0.2. Zniwelować uchyb, korzystając ze współczynnika kp.
Czy możliwe jest zniwelowania uchybu statycznego? (wartość zadana =1)
Czy możliwe byłoby w układzie otwartym?
Zarejestrować odpowiedzi na skok jednostkowy.
Następnie zmienić wartość zakłócenia na 'rand(1)' i ponownie wykonać regulację.
Czy możliwe jest zniwelowania uchybu statycznego?

4.5 Regulacja układu członem całkującym
Włączyć do układu człon całkujący, powtórzyć regulację korzystając ze współczynnika ki.
W polu 'zakłócenia' wprowadzić wartość 0.2. Zniwelować uchyb, korzystając ze współczynnika ki.
Czy możliwe jest zniwelowania uchybu statycznego? (wartość zadana =1)
Czy możliwe byłoby w układzie otwartym?
Zarejestrować odpowiedzi na skok jednostkowy.
Następnie zmienić wartość zakłócenia na 'rand(1)' i ponownie wykonać regulację.
Czy możliwe jest zniwelowanie uchybu statycznego?

4.6 Badanie jakości regulacji
W układzie zamkniętym z członami proporcjonalnym oraz całkującym, i stałym zakłóceniem
wykreślić co najmniej 4 odpowiedzi na skok jednostkowy. Dla zarejestrowanych przebiegów
wyznaczyć: uchyb statyczny (ustalony), czas regulacji oraz przeregulowanie.

8

5 Zakres sprawozdania

Sprawozdanie powinno zawierać następujące nagłówki i odpowiedzi na poniższe pytania:
1. Sterowanie w układzie otwartym
- jaki jest wpływ poszczególnych stałych czasowych oraz współczynnika wzmocnienia na
odpowiedź obiektów n-tego rzędu na skok jednostkowy?
2. Kryterium Nyquista
- należy zamieścić równanie transmitancji badanego układu otwartego oraz zamkniętego. Dla
obydwu układów zamieścić charakterystyki: odpowiedź na skok jednostkowy oraz charakterystyki
częstotliwościowe.
- należy przestawić nanieść pierwiastki wielomianu charakterystycznego na płaszczyznę zespoloną.
Co można powiedzieć o stabilności układu na podstawie położenia tych pierwiastków?
3. Wyznaczenie zapasu stabilności w układzie zamkniętym z regulatorem proporcjonalnym
- co to jest zapas stabilności i jak się go wyznacza? jaki jest wpływ współczynnika kp na zapas
stabilności? czy przy zastosowaniu różnych metod wyznaczania zapasu stabilności otrzymano
jednakowe wyniki? Jeśli nie dlaczego?
4. Wyznaczenie zapasu stabilności w układzie zamkniętym z regulatorem całkującym
-jaki jest wpływ współczynnika ki na zapas stabilności? czy przy zastosowaniu różnych metod
wyznaczania zapasu stabilności otrzymano jednakowe wyniki? Jeśli nie dlaczego?
5. Regulacja układu członem proporcjonalnym
Jakie jest regulacyjne członu proporcjonalnego? Czy możliwe jest zniwelowania uchybu
statycznego?
W układzie zamkniętym lub otwartym?
6. Regulacja układu członem całkującym
Jakie jest regulacyjne członu całkującego? Czy możliwe jest zniwelowania uchybu statycznego?
W układzie zamkniętym lub otwartym?
7. Badanie jakości regulacji
Jaki jest wpływ współczynników kp i ki na uchyb statyczny (ustalony) czas regulacji oraz
przeregulowanie? Jaka jest zależność między przeregulowaniem a zapasem stabilności?
8. Badanie sterowalności, obserwowalności i stabilności
Dla układu wyrażonego poniższą transmitancją wyznaczyć stabilność, sterowalności i
obserwowalność:

0

1

2

2

3

3

)

(

T

s

T

s

T

s

T

kp

s

G









Wartości współczynników przyjąć jak na laboratorium.
Czy układ jest sterowalny, obserwowalny i stabilny dla dowolnego kp?

9

6 Literatura pomocna do wykonania ćwiczenia, przygotowania sprawozdania i przygotowania
się do zaliczenia:

1. Brzózka J., Ćwiczenia z automatyki w MATLABIE i SIMULINKU, Mikom, Warszawa, 1997.
2. Dębowski A.: Automatyka. Podstawy teorii, WNT, Warszawa 2008.
3. Frelek B. i inni, Laboratorium podstaw automatyki, W PW, 1984.
4. Mrozek B+Z, Matlab 5.x i Simulink 2.x, Wydawnictwo PLJ, Warszawa 1998.
5. Nowacki P., Szklarski L., Górecki H.: Podstawy teorii układu regulacji autonomicznej. Tom I,

PWN, Warszawa 1970.

6. Pełczewski W., Teoria sterowania, WNT, Warszawa 1980.
7. Żelazny M., Podstawy automatyki, PWN, Warszawa 1976.
8. Badania obiektów dynamicznych (z zastosowaniem programu MATLAB) - Przykłady

programów do wykonania w czasie zajęć laboratoryjnych. Opracowanie WTPW, Warszawa
2002.