Pasmowy model ciała stałego to teoria opierająca objaśnienie własności ciał stałych na założeniu, że energie elektronów wchodzących w ich skład nie są dowolne, lecz należą do ściśle określonych zakresów, zwanych dozwolonymi pasmami energetycznymi. Pasma te są rozdzielone wzbronionymi pasmami energetycznymi tzn. Zakresami wartości energii, których nie może mieć żaden elektron znajdujący się w ciele stałym. Pasmowy model ciała stałego opiera się na następujących podstawowych założeniach:

• ciało stałe stanowi kryształ idealnie periodyczny

• położenia atomów w węzłach sieci krystalicznej są praktycznie niezmienne, a ich ruchy polegają na nieznacznych drganiach

• ruch ogromnej liczby cząstek i ich wzajemne oddziaływanie są równoważne ruchowi jednej cząstki w uśrednionym polu wszystkich pozostałych

W ćwiczeniu mamy do czynienia ze złączem prostującym, czyli złączem wykazującym nieliniową, asymetryczną względem napięcia charakterystykę prądowo napięciową. Warunkiem koniecznym, aby kontakt miał własności prostujące, jest istnienie pomiędzy dwoma stykającymi się materiałami warstwy zaporowej. Warstwa taka powstaje przy kontakcie metalu z półprzewodnikiem oraz przy złączeniu dwóch półprzewodników o różnym typie przewodnictwa, dając wówczas złącze n-p. W przypadku styku metalu z półprzewodnikiem typu n, w chwili zetknięcia elektrony z półprzewodnika przechodzą do metalu. Poziomy Fermiego w metalu i półprzewodniku wyrównują się. Zjonizowane donory utrzymują elektrony w metalu w pobliżu styku, co uniemożliwia dopływ elektronów z wnętrza półprzewodnika w pobliże styku. Powstaje w ten sposób warstwa kontaktowa prawie pozbawiona elektronów, czyli warstwa zaporowa o pewnej wysokości i szerokości bariery potencjału. Przyłożenie napięcia dodatniego do metalu powoduje obniżenie bariery, a co za tym idzie łatwiejszy przepływ elektronów i opór warstwy zaporowej maleje. Przy takiej polaryzacji kontaktu mamy kierunek dobrego przewodzenia. Polaryzacja odwrotna podwyższa barierę, utrudniając przepływ elektronów i opór warstwy rośnie. Przy takiej polaryzacji mamy kierunek zaporowy. Mechanizm powstawania warstwy zaporowej na złączy n-p jest analogiczny jak w przypadku złącza metal półprzewodnik.

Charakterystyka prądowo napięciowa prostownika.

Idealny prostownik Rzeczywisty prostownik

Prostownik napięcia to układ elektryczny służący do zamiany napięcia zmiennego na napięcie stałe. Wykorzystuje się do tego celu własność jednokierunkowego przewodzenia prądu przez diode próżniową lub diodę półprzewodnikową. Jeśli dioda zostanie dołączona do obwodu prądu zmiennego to prąd w obwodzie będzie przepływał tylko w ciągu tych półokresów, dla których anoda w diodzie próżniowej lub złącze p. diody półprzewodnikowej będzie miała potencjał dodatni względem katody lub złącza n. Dlatego prąd w obwodzie nie będzie już zmienny lecz pulsujący. W celu wykorzystania obu półokresów prądu zmiennego stosuje się układy prostowania dwupołówkowego. Na schematach przedstawiono odpowiednio prostownik napięcia jednopołówkowy, dwupołówkowy i Graetza.

Schemat układu pomiarowego.

Tabela odczytów.

	Kierunek przewodzenia		Kierunek zaporowy
	U	I	U	I
Klasa miernika
Zakres pomiarowy
Wartość najmniejszej działki
Niepewność pomiarowa

Tabela pomiarowa.

Prostownik selenowy.
Kierunek przewodzenia		Kierunek zaporowy
U [V]	I [mA]	U [V]	I [mA]

Obliczanie oporu z prawa Ohma dla napięcia 1V.

	Kierunek przewodzenia	Kierunek zaporowy
ΔR
δR

	Kierunek przewodzenia		Kierunek zaporowy
	U	I	U	I
Klasa miernika	0,5	1	0,5	1
Zakres pomiarowy	3 V	60 mA	3 V	0,06 mA
Wartość najmniejszej działki	0,1 V	0,5 mA	0,1 V	0,0005 mA
Niepewność pomiarowa	0,065[V]	0,85[mA]	0,065[V]	0,00085[mA]

Tabela pomiarowa.

Prostownik selenowy.
Kierunek przewodzenia		Kierunek zaporowy
U [V]	I [mA]	U [V]	I [mA]
0	0	0	0
0,1	0	0,2	0,0005
0,2	0	0,4	0,001
0,3	0,5	0,6	0,0015
0,4	1,5	0,8	0,002
0,5	3,5	1,0	0,003
0,6	7,	1,2	0,004
0,7	10	1,4	0,0045
0,8	14	1,6	0,0055
0,9	18	1,8	0,007
1,0	22	2,0	0,008
1,1	27	2,2	0,0095
1,2	31	2,4	0,011

Obliczanie oporu z prawa Ohma dla napięcia 1V.

	Kierunek przewodzenia	Kierunek zaporowy
ΔR	4,7 Ω	116,1 kΩ
δR	10,3 %	34,8 %

Obliczenia dla kierunku przewodzenia:

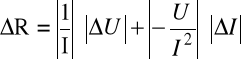
Obliczenia dla kierunku zaporowego:

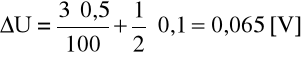
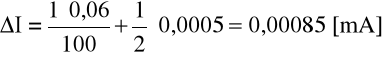
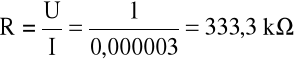
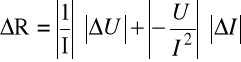
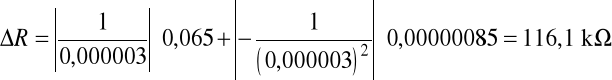
Wnioski:

Celem ćwiczenia jest wyznaczenie charakterystyki prostownika selenowego. W tym celu badaniu poddana zastała dioda przez którą przepływał prąd w kierunku przewodzenia i w kierunku zaporowym. Z otrzymanych wyników widać, że w kierunku przewodzenia wraz ze wzrostem napięcia przyrost prądy jest znaczny, więc element wykazyje małą rezystywność w kierunku przewodzenia. Jeśli chodzi o kierunek zaporowy, to należy powiedzieć, iż badany element wykazuje dużą rezystancję, gdyż pomimo wzrostu napięcia przyrost prądu jest znikomy. .

Korzystając z prawa Ohma, została w ćwiczeniu wyliczona rezystancja przy napięciu 1 V dla kierunku przewodzenia i dla kierunku zaporowego. Różnica pomiędzy nimi była bardzo dużą, gdyż dla kierunku przewodzenia rezystancja wynosiła 45,45 Ω, a dla kierunku zaporowego aż 333,3 kΩ. Błędy pomiarowe spowodowane są błędem podczas pomiaru napięcia. Woltomierz użyty do pomiarów miał zakres 3 V, a błąd wyznaczenia oporu ΔR obliczony został dla wartości napięcia 1V czyli dla wartości znajdującej się poniżej połowy skali. Z wykresu I=f(U) widać również, że badany element nie jest elementem liniowym.

---