1. Definicja układu regulacji automatycznej - schemat blokowy, wyjaśnienie podstawowych pojęć (rysunek).

Schematy blokowe - układy sterowania mogą składać się z pewnej liczby podzespołów. Schemat blokowy układu jest graficznym opisem funkcji wykonywanych przez każdy element i przepływające sygnału.
a) blok funkcjonalny

x₁(s) x₂(s)

G(s)

x₂(s) = G(s)x₁(s)

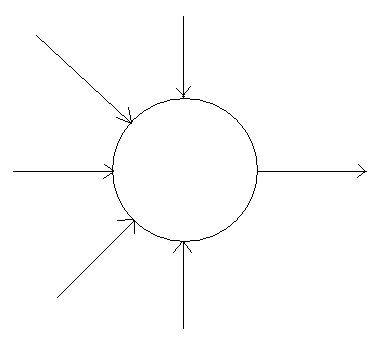
b) węzeł sumacyjny

x₁(s)
x₂(s)
+
-


x₃(s) + x₀(s)



-
x₄(s)
+
x₅(s)





c) węzeł zaczepowy

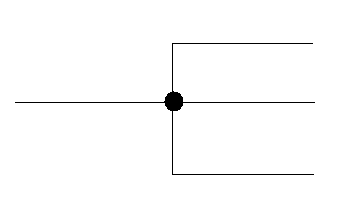
x(s)







2. Podział układu regulacji ze względu na sposób opisu matematycznego.

- ciągłe, dyskretne, logiczne
- liniowe, nieliniowe
- stacjonarne, niestacjonarne
- o parametrach skupionych i rozłożonych

3. Podział układu regulacji ze względu na zadania układu.

- układy stabilizacji (ω ≠ const.)
- układy śledzące (ω = ω(x))
- układy optymalne
- układy przełączające

4. Transmitancja.

Transmitancja jest to stosunek obrazu funkcji wyjściowej do obrazu funkcji wejściowej.

G(s) = y(s) / a(s)

f(t) F(s) = L[f(t)] = ʃ₀^∞ f(t)e^-stdt

s = a + jiω

5. Układ sterowania zamknięty i otwarty.

a) otwarty układ sterowania

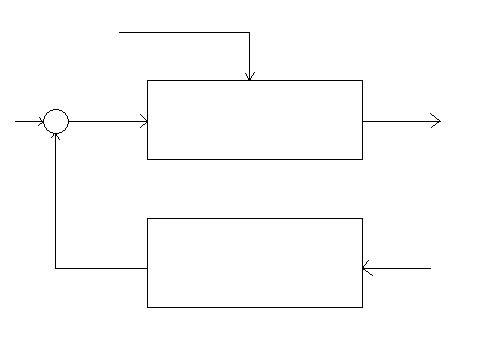
z_i




z obiekt y
sterowania
+ -


u

urządzenie
sterujące w

b) zamknięty układ sterowania

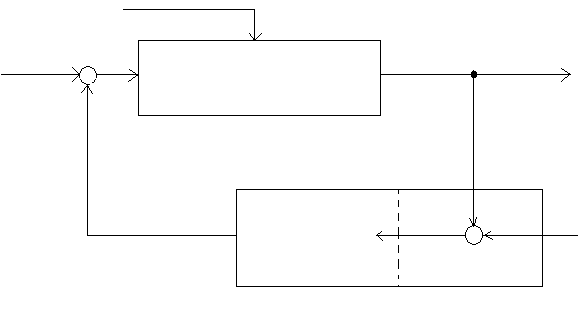
z_i



z obiekt sterowania y

+ -



u
-
e + w
regulator

6. Metody opisu właściwości dynamicznych.

1. równanie różniczkowe

2. równanie różnicowe

3. przestrzeń stanu

4. transmitancja

5. metody graficzne
   - skokowe
   - impulsowe
   - sinusoidalne
   * charakterystyka amplitudowo-fazowa
   * charakterystyka amplitudowa i fazowa we współrzędnych logarytmicznych

6. algebra Boole'a

7. Przekształcenie Laplace'a.

a) δ(t) 1

b) skok jednostkowy 1(t) 1/s

c) t^n-1 / (n-1)! (n=1,2,3,…) 1/sⁿ

d) t^n-1e^-at/(n-1)! 1/(s+a)ⁿ

e) sinωt ω/s²+ω²

f) cosωt s/s²+ω²

g) e^-atsinωt ω/(s+a)²+ω²

h) e^-atcosωt s+a/(s+a)²+ω²

8. Przekształcenia formy sygnału.

9. Ogólne równanie ruchu.

dopływ - odpływ = akumulacja

d^my/dt^m + a₁(d^m-1y/dt^m-1) + … + a_m-1*dy/dt + a_my = b₀(d^ry/dt^r) + b₁(d^r-1u/dt^r-1) + … + b_r-1(dy/dt) + b_ru

10. Człon statyczny 0. rzędu (proporcjonalny) i całkujący (równanie, współczynnik wzmocnienia, transmitancja, wykres odpowiedzi skokowej, przykład)

y = b₀u - równanie

k = b₀ - współczynnik wzmocnienia

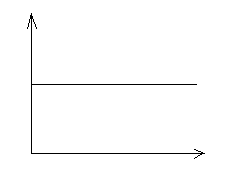
y(t)

k

G(s) = k

t


m n

Δy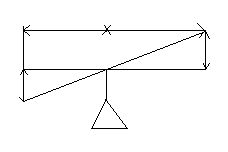

Δu

k = n/m

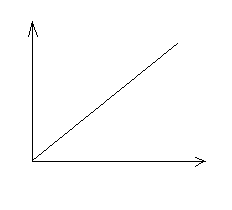
y(t)

G(s) = k/sT₁

t

11. Człon statyczny pierwszego rzędu („inercyjny”) i opóźniający

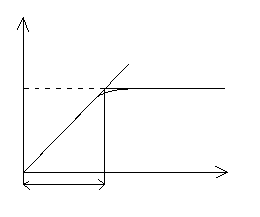
y(t)

G(s) = k/T_s+1

k G(s) = y(s)/M(s) = b₀/s+a₁ = (b₀/a₁)/(1/a₁s+1)

= k/(T_s+1)

np. Zbiornik ze swobodnym przepływem

T t

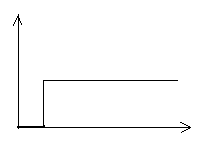
y(t)
G(s) = k*e^-sT0

równanie nieliniowe : y(t)={1 t≥τ ; 0 t<τ

k G(s) = e^-τs

np. rurociąg

T₀ t

12. Człon rzeczywisty i idealny (…)

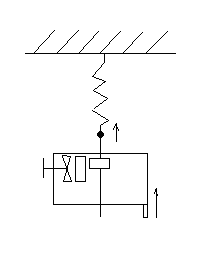
C

dy/dt +e₁y = b₀ du/dt

k = 0

y G(s) = T_bS/T_s+1

r

x

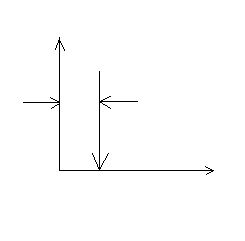
y

Δ0 y = b₀ du/dt + 0_n

k = 0

G(s) = T_dS dla T_d = b₀

y(t) = δ(t)

t

13. Człon 2. rzędu oscylacyjny (bez równania przebiegu odpowiedzi - analiza przebiegów), człon opóźniający.

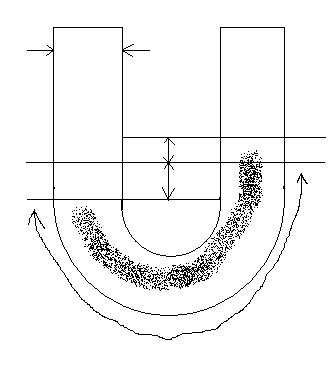
P₁x P₂x

d

d²y/dt² + a₁*(dy/dt) + a₂y = b₀u

G(s) = 1/T²S²+2εT_s+1
y
Δ<0 wpada w drganie
y








l

---