Liczby zespolone - liczby będące elementami rozszerzenia ciała liczb rzeczywistych o jednostkę urojoną i. Każda liczba zespolona z może być zapisana w postaci z = a + bi, gdzie a,b są pewnymi liczbami rzeczywistymi, nazywanymi odpowiednio częścią rzeczywistą oraz częścią urojoną liczby z. Działania: 1)dodawanie z1+z2=(x1,y1)+(x2,y2)=(x1+x2,y1+y2) 2)mnożenie z1*z2=(x1,y1)*(x2,y2)=(x1x2-y1y2,x1y2+x2y1) Postać algebraiczna(kanoniczna)- z=a+bi Rez=a(część rzeczywista; Imz=b(częśc urojona) Postać trygonometryczna- z=a+bi=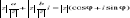 Wzór Moivrea-jest wzorem na n-tą potęgę liczby zespolonej zapisanej w postaci trygonometrycznej 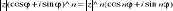Macierz-funkcja, która uporządkowanym parom (i,j) przyporządkowuje odpowiednią liczbę rzeczywistą lub zespoloną Twierdzenie Laplacea- dowolny wyznacznik jest równy sumie iloczynów elementów dowolnego wiersza (dowolnej kolumny) i ich dopełnień algebraicznych 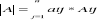i- jest ustalone i określa wiersz macierzy, wzgl którego następuje rozwinięcie aij- element macierzy w j-tym wierszu i j-tej kolumnie Aij- dopełnienie algebraiczne elementu aij. Twierdzenie Laplace'a pozwala obliczyć wyznacznik macierzy unikając korzystania z bardzo czasochłonnej metody opartej na definicji wyznacznika. Twierdzenie Cramera- układ Cramera ma dokładnie jedno rozwiązanie. Jest ono dane wzorem: 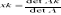k=1,2,3,…,n Ak-powstaje z macierzy A przez zastąpienie k-tej kolumny kolumną wyrazów wolnych Twierdzenie Kroneckera-Capellego-układ równań liniowych o macierzy głównej A i macierzy rozszerzonej U ma rozwiązanie wtedy i tylko wtedy gdy rz(A)=rz(U) gdzie rz(A),rz(U) oznaczają odpowiednio rzędy macierzy A oraz U Iloczyn skalarny-operator na przestrzeni liniowej przypisujący dwóm argumentom (wektorom) tej przestrzeni rzeczywistą wartość skalarną. Iloczyn skalrny wektorów a i b można wyliczyc znając długości wektorów ai boraz kąt alfa między wektorami a°b=a*b*cos alfa Cosinusy kierunkowe- liczby opisujące kierunek wektora w przestrzeni Kąt między wektorami cos alfa= a°b/⊥*b Iloczyn wektorowy- axb wektorów a,b nazywamy wektor w spełniający warunki: w⊥a, w⊥b; w=ab*sin kąta(a,b); orientacja trójki wektoru a,b,w jest zgodna z orientacją współrzędnych Iloczyn mieszany-iloczynem m. uporządkowanej trójki wektorów a,b,c nazywamy liczbę określoną wzorem: (a x b)°c. Własności: (a x b)°c=(b x c)°a; (a x b)°c= -(b x a)°c; (alfa a x b)°c= alfa(a x b)°c; wektory leżą w tej samej płaszczyźnie gdy (a x b)°c=0

Warunek równoległości dwóch płaszczyzn- dane są płaszczyzny 1:A1x+B1y+C1z+D1=0 i 2:A2x+B2y+C2z+D2=0 -> 12 <-> n1n2 <-> A1/A2=B1/B2=C1/C2=k≠0 n1=[A1,B1,C1] n2=[A2,B2,C2] Warunek prostopadłości 2 płaszczn- n1⊥n2<-> n1°n2=0<-> A1A2+B1B2+C1C2=0 Warunek prostopadłości 2 wektorów- a⊥b<-> cos alfa (a,b)=0<-> a°b=0 Warunek równoległości 2 wektorów- ab<-> istnieje taka liczba rzeczywista t (t R, t≠0) że a=t°b tzn ax/bx=ay/by=Az/bz=t Równanie prostej parametryczne- [x,y,z]=[xo+ta,yo+Tb, zo+Tc] t należy R Równanie pr. Kierunkowej- t=x-xo/a=y-yo/b=z-zo/c Równanie prostej krawędziowej- układ równań A1x+B1y+C1z+D1=0 i A2x+B2y+C2z+D2=0 Warunek równoległości prostej- l1l2<-> u1u2<-> a1/a2=b1/b2=c1/c2=k k nal. R k≠0 Warunek prostopadłości prostej- l1⊥l2<-> u1⊥u2<-> a1a2+b1b2+c1c2=0 Ciąg liczbowy- ciągiem l. nazywamy funkcję określoną na zbiorze liczb naturalnych (tzn. że dziedzina to l. naturalne) o wartościach w zbiorze liczb rzeczywistych lub zespolonych an: N-> R( C ) N={1,2,3,4,…} Def ciągu rosnącego- dla każdego n naturalnego: an+1-an>0 Def ciągu malejącego- dla każdego n naturalnego: an+1-an<0 Ciąg ograniczony- to ciąg którego wszystkie wyrazy należą do pewnego przedziału skończonego. Ograniczony z góry- jeżeli jego wszystkie wyrazy są mniejsze od pewnej ustalonej liczby. Ograniczony z dołu-większe od ostalonej liczby Asymptoty poziome- istnieją wtedy gdy granica funkcji ±∞ jest właściwa(jest konkretną liczbą g należy R). As.poz. Mają równanie: y=g; g=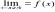 Asymptoty pionowe- istnieją w punktach nie należących do dziedziny funkcji, w których granice są niewłaściwe (±∞). Asymt.pion. Mają równania: x=xo, x=x1, x=x2 itd.. Asymptoty ukośne- mają równanie: y=ax+b (jeżeli funkcja ma asympt.poz. To nie może już mieć asympt.ukośnej i odwrotnie) Różniczka funkcji- f w punkcie xo nazywamy funkcję df zmiennej Δx=x-xo określoną wzorem df(Δx):=f'(xo)*Δx

Zastosowanie różniczki- jeśli funkcja f ma pochodną właściwą w punkcie xo, to f(xo+Δx)≈f(xo)+f'(xo)Δx Twierdzenie Lagrange'a- jedno z kilku twierdzeń o wartości średniej w rachunku różniczkowym. Tw: jeśli dana funkcja f:R->R jest: ciągła w przedziale [a,b]; różniczkowalna w przedziale (a,b), to istnieje taki punkt c należący (a,b) że: f(b)-f(a)/b-a=f'( c) Twierdzenie Rolle'a- funkcja różniczkowalna która przyjmuje równe wartości w 2 punktach musi mieć punkt gdzie nachylenie prostej stycznej do wykresu funkcji jest równe zeru f'(c )=0 Twierdzenie Cauchy'ego- jest uogólnieniem twierdzenia Lagrange'a. Tw: jeżeli dane funkcje f i g są: ciągłe w przedziale domkniętym [a,b]; różniczkowalne w przedziale (a,b), to istnieje punkt c należący do przedziału (a,c) taki że: g'(c )*[f(b)-f(a)]=f'(c )* [g(b)-g(a)] Twierdzenie Taylora- niech Y będzie przestrzenią unormowaną. Załóżmy, że f:[a,b]->Y jest (n+1) razy różniczkowalna na [a,b] w sposób ciągły. Wówczas dla każdego x należącego do (a,b) Rn(x,a) spełnia warunek lim (x->a) Rn(x,a)/(x-a)^n=0 Rn(x,a)-nazywamy resztą Peano we wzorze Taylora

---