Metody i algorytmy sterowania cyfrowego |
||
Wydział Elektryczny Semestr V |
||
Piotr Gajewski 170755
|
Ćwiczenie : Filtry NOI i SOI
|
Termin zajęć: Czwartek N 9-11 |
|
|
Ocena: |
22.11.2010r. |
|
|
1. Filtry cyfrowe są tworzone jako urządzenia spełniające pewną matematyczną funkcję na sygnale wejściowym x(n) dając na wyjściu sygnał y(n). Filtry analogowe i cyfrowe charakteryzuje kilka własności z których najważniejsze to:
- dynamika czyli jak dobrze tłumi nasz filtr w paśmie zaporowym
- częstotliwość graniczna lub dwie częstotliwości graniczne gdy mamy do czynienia z filtrem pasmowym.
- szerokość zbocza (krawędź) czyli jak "szybko" filtr tłumi
Ze względu na pasmo przenoszenia rozróżniamy filtry:
- górnoprzepustowy
- dolnoprzepustowy
- środkowoprzepustowy
- środkowozaporowy
Celem laboratorium było zaprojektowanie filtru SOI i NOI dolnoprzepustowego.
Rys1.1 Charakterystyka amplitudowa filtru dolnoprzepustowego
1.1. Filtry SOI- Filtr o skończonej odpowiedzi impulsowej to rodzaj filtru cyfrowego, który charakteryzuje się tym, że jego odpowiedź na dany ciąg wejściowych próbek ma skończoną długość. Odpowiedź impulsowa filtru SOI i jego współczynniki są takie same. Układy te są zawsze stabilne i charakteryzują się liniowymi charakterystykami fazowymi.
1.2 Filtry NOI- filtry rekursywne o nieskończonej odpowiedzi impulsowej. Znaczy to tyle, że reakcja na pobudzenie o skończonym czasie trwania jest teoretycznie nieskończenie długa. Jest to efektem występowania pętli sprzężenia zwrotnego
1.3 Metoda przekształcenia bilingowego
![]()
![]()
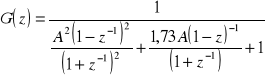
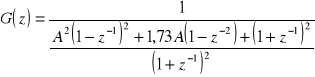
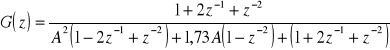
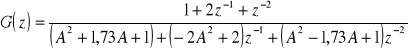
2. Synteza i analiza filtru rekursywnego NOI dolnoprzepustowego.
Kod programu w Matlabie ( Dane są przeliczone w zależności od grupy . gr4 )
a) Charakterystyka amplitudowa filtru dolnoprzepustowego Rys 2.1
%Kod Programu
fp=1400
fgc=240
wgc=2*pi*fgc
Tp=1/fp
wga=0.7874
A=wga*(1/tan(wgc*Tp/2))
L=[1]
M=[1 1.73 1]
[H,W]=freqs(L,M)
plot(W, abs(H)); grid on
Rys 2.1
b) Charakterystyka fazowa filtru dolnoprzepustowego Rys 2.2
%kod programu
fp=1400
fgc=240
wgc=2*pi*fgc
Tp=1/fp
wga=0.7874
A=wga*(1/tan(wgc*Tp/2))
L2=[1 2 1]
M2=[A^2+A*1.73+1 -2*A^2+2 A^2-A*1.73+1]
[H,F]=freqz(L2,M2,512,fp)
plot(F,abs(H)); grid on
Rys 2.2
c) Opóźnienie fazowe filtru dolnoprzepustowego Rys 2.3
%kod Programu
fp=1400
fgc=240
wgc=2*pi*fgc
Tp=1/fp
wga=0.7874
A=wga*(1/tan(wgc*Tp/2))
L2=[1 2 1]
M2=[A^2+A*1.73+1 -2*A^2+2 A^2-A*1.73+1]
phasedelay(L2,M2,512,fp)
Rys 2.3
d) Charakterystyka fazowa Rys 2.4
figure(3)
P=angle(H)*180/pi %charakterystyka fazowa
plot(W,P)
grid on
Rys 2.4
e) Odpowiedź na skok jednostkowy Rys 2.5
%kod programu
fp=1400
fgc=240
wgc=2*pi*fgc
Tp=1/fp
wga=0.7874
A=wga*(1/tan(wgc*Tp/2))
L2=[1 2 1]
M2=[A^2+A*1.73+1 -2*A^2+2 A^2-A*1.73+1]
[o,ts]=stepz(L,M);
plot(ts,o)
grid on
Rys 2.5
3. Synteza i analiza cyfrowych filtra nierekursywnego SOI dolnoprzepustowego
Parametry filtru
częstotliwość próbkowania
![]()
![]()
Częstotliwość odcięcia musi być wieloktortnoscią 50 Hz wiec przyjąłem
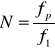
długość okna filtru
a) Działka dyskretnych sekwencji filtru dolnoprzepustowego Rys 3.1
%kod programu
fp=1400;
fodc=250;
f1=50;
N=fp/f1
deltaf=fp/N
H=[exp(-i*(0:5)*pi*(N-1)/N),zeros(1,17),exp(i*((N-(22:27))*pi*(N-1)/N))]
figure(1)
stem(0:N-1,abs(H))
Rys 3.1
b) Charakterystyka odpowiedzi impulsowej filtru dolnoprzepustowego Rys 3.2
fp=1400;
fodc=250;
f1=50;
N=fp/f1
deltaf=fp/N
H=[exp(-i*(0:5)*pi*(N-1)/N),zeros(1,17),exp(i*((N-(23:27))*pi*(N-1)/N))]
L=ifft(H)
impz(L,1)
Rys 3.2
b')
fp=1400;
fodc=250;
f1=50;
N=fp/f1
deltaf=fp/N
H=[exp(-i*(0:5)*pi*(N-1)/N),zeros(1,17),exp(i*((N-(23:27))*pi*(N-1)/N))]
stem(0:N-1,L)
c) Opóźnienie fazy Rys 3.3
figure(4)
phasedelay(L,M,512,fp);
Rys 3.3
freqz(L,1,512,fp);
phasedelay(H,L)
d) Charakterystyka widmowa filtru dolnoprzepustowego Rys 3.4
%kod programu
fp=1400;
fodc=250;
f1=50;
N=fp/f1
deltaf=fp/N
H=[exp(-i*(0:5)*pi*(N-1)/N),zeros(1,17),exp(i*((N-(23:27))*pi*(N-1)/N))]
[H,F]=freqz(L,1,512,fp);
plot(F,abs(H))
Rys 3,4
e) Charakterystyka widmowa filtru dolnoprzepustowego po dodaniu okna wygładzającego Rys 3.5
%kod programu
fp=1400;
fodc=250;
f1=50;
N=fp/f1
deltaf=fp/N
H=[exp(-i*(0:5)*pi*(N-1)/N),zeros(1,17),exp(i*((N-(23:27))*pi*(N-1)/N))]
Lw=L.*hamming(N)';
[H,F]=freqz(Lw,1,512,fp);
plot(F,abs(H))
Rys 3.5
f) charakterystyka częstotliwościowa Rys 3.6
%kod programu
fp=1400;
fodc=250;
f1=50;
N=fp/f1
deltaf=fp/N
H=[exp(-i*(0:5)*pi*(N-1)/N),zeros(1,17),exp(i*((N-(23:27))*pi*(N-1)/N))]
Lw=L.*hamming(N)';
[H,F]=freqz(Lw,1,512,fp);
plot(F,abs(H))
figure(6)
P=angle(H)*180/pi;
plot(F,P);
grid on
Rys 3.6
filtracja sygnału zaszumianego filtrem NOI oraz SOI
Sygnał zaszumiany
a)
%kod programu
fp=1400;
fodc=250;
f1=50;
N=fp/f1
deltaf=fp/N
t=(0:(1/fp):0.16);
signal=5*sin(100*pi*t)+2.5*sin(2*pi*(fodc+150)*t);
plot(t,signal)
grid on;
b)
%kod programu
fp=1400;
fodc=250;
f1=50;
N=fp/f1
deltaf=fp/N
t=(0:(1/fp):0.16);
signal=5*sin(100*pi*t)+2.5*sin(2*pi*(fodc+150)*t);
Le = length(t)-1;
signal1 = abs(fft(signal))/(Le/2);
ff = 0:(fp./Le):fp;
figure(7);
plot(ff,signal1)
grid on;
Filtrowanie NOI
a)
%kod programu
fp=1400
fgc=240
wgc=2*pi*fgc
Tp=1/fp
wga=0.7874
A=wga*(1/tan(wgc*Tp/2))
L2=[1 2 1]
M2=[A^2+A*1.73+1 -2*A^2+2 A^2-A*1.73+1]
fp=1400;
fodc=250;
f1=50;
N=fp/f1
deltaf=fp/N
t=(0:(1/fp):0.16);
signal=5*sin(100*pi*t)+2.5*sin(2*pi*(fodc+150)*t);
signal1_f = filter(L,M,signal);
plot(t,signal1_f)
grid on;
b)
%kod programu
fp=1400
fgc=240
wgc=2*pi*fgc
Tp=1/fp
wga=0.7874
A=wga*(1/tan(wgc*Tp/2))
L2=[1 2 1]
M2=[A^2+A*1.73+1 -2*A^2+2 A^2-A*1.73+1]
fp=1400;
fodc=250;
f1=50;
N=fp/f1
deltaf=fp/N
t=(0:(1/fp):0.16);
signal=5*sin(100*pi*t)+2.5*sin(2*pi*(fodc+150)*t);
signal1_fw = abs(fft(signal1_f))/(Le/2);
plot(ff,signal1_fw)
grid on;
Filtrowanie SOI
fp=1400;
fodc=250;
f1=50;
N=fp/f1
deltaf=fp/N
H=[exp(-i*(0:5)*pi*(N-1)/N),zeros(1,17),exp(i*((N-(23:27))*pi*(N-1)/N))]
L=ifft(H);
signal1_f = filter(L,H,signal);
plot(t,signal1_f)
grid on;
To bzduuuuraa ? !!!!!
Wyszukiwarka
Podobne podstrony:
sprawko algorytmy last
nieodporny sprawozdanie, Pwr, Metody i algorytmy sterowania cyfrowego, sprawka
sprawozdanie filtr Noi, Pwr, Metody i algorytmy sterowania cyfrowego, sprawka
moje sprawka, Metody sprawko 3, LABORATORIUM METOD I ALGORYTMÓW STEROWANIA CYFROWEGO
sprawko cw 2, Pwr, Metody i algorytmy sterowania cyfrowego, sprawka
nieodporny sprawozdanie, Pwr, Metody i algorytmy sterowania cyfrowego, sprawka
Układy Napędowe oraz algorytmy sterowania w bioprotezach
5 Algorytmy
5 Algorytmy wyznaczania dyskretnej transformaty Fouriera (CPS)
Tętniak aorty brzusznej algorytm
Algorytmy rastrowe
Algorytmy genetyczne
Teorie algorytmow genetycznych prezentacja
Algorytmy tekstowe
Algorytmy i struktury danych Wykład 1 Reprezentacja informacji w komputerze
ALGORYTM EUKLIDESA
więcej podobnych podstron