Zestawienie wyników:
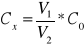
Stężenie obliczone z wzoru:Ocena statystyczna wartości skręcalności optycznej:
Odrzucam wyniki niepewne testem Q Dixona
R=Xn-X1=53,339-46,255=7,084
Q1= X2-X1/R=(47,915-46,255)/ 7,084=0,234
Qn= Xn-Xn-1/R=(53,339-51,766)/7,084=0,222
Qtab(P=95%,n=10)=0,412
Średnia arytmetyczna: X = ΣX/n = 498,386/10 = 49,8386
Wariancja: S2= Σ(X-X)2/n-1 = 39,50732/9 = 4,389702
Ochylenie standardowe próby: S√ S2= 2,0952
Odchylenie standardowe śr.arytmetycznej S=S/√n= 0,666
Obliczamy współczynnik regresji ze wzoru
Obliczamy wyraz wolny ze wzoru
Równanie regresji liniowej
Obliczamy odchylenie standardowe regresji
Nr. Próby |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
V roztworu |
7 |
14 |
21 |
28 |
35 |
42 |
49 |
56 |
63 |
70 |
C Roztworu |
0,007 |
0,014 |
0,021 |
0,028 |
0,035 |
0,042 |
0,049 |
0,056 |
0,063 |
0,07 |
f |
1,75 |
3,63 |
5,55 |
8,08 |
9,25 |
11,15 |
13,2 |
15,68 |
17,63 |
19,23 |
f*0,342 |
0,5985 |
1,24146 |
1,8981 |
2,7634 |
3,1635 |
3,8133 |
4,5144 |
5,3626 |
6,0295 |
6,5767 |
Skręcalność właściwa |
46,255 |
47,915 |
48,855 |
53,339 |
48,86 |
49,073 |
49,796 |
51,766 |
51,734 |
50,788 |
C11 |
0,007 |
C12 |
0,014 |
C13 |
0,021 |
C14 |
0,028 |
C15 |
0,035 |
C16 |
0,042 |
C17 |
0,049 |
C18 |
0,056 |
C19 |
0,063 |
C110 |
0,07 |
![]()
2.2 Skręcalność właściwa obliczona ze wzoru:
|
46,255 |
|
47,915 |
|
48,855 |
|
53,339 |
|
48,865 |
|
49,073 |
|
49,796 |
|
51,766 |
|
51,734 |
|
50,788 |
Z={46,255; 47,915; 48,855; 48,865; 49,073; 49,796; 50,788; 51,734; 51,766; 53,339}
Wnioski: Qn, Q1< Qtab z prawdopodobieństwem P=95% wszystkie wyniki skręcalności właściwej należą do zbioru Z
2,2 Obliczamy średnią arytmetyczną i wariancję:
nr |
X |
X-X |
(X-X)2 |
1 |
46,255 |
-3,5836 |
12,84219 |
2 |
47,915 |
-1,9236 |
3,700237 |
3 |
48,855 |
-0,9836 |
0,967469 |
4 |
48,865 |
-0,9736 |
0,947897 |
5 |
49,073 |
-0,7656 |
0,586143 |
6 |
49,796 |
-0,0426 |
0,001815 |
7 |
50,788 |
0,9494 |
0,90136 |
8 |
51,734 |
1,8954 |
3,592541 |
9 |
51,766 |
1,9274 |
3,714871 |
10 |
53,339 |
3,5004 |
12,2528 |
SUMA |
498,386 |
|
39,50732 |
2,3 Obliczamy przedział ufności zmiennej X, oceniamy na podstawie istotności α=0,05
X-S*tα,n-1<μx< X+S*tα,n-1
tα,n-1=t0,05,8=2,31
S*tα,n-1 = 0,666*2,31=1,53846
49,8386-1,53846<μx<49,8386+1,53846
48,30014<μx<51,37706
= 49,8386 1,53846
3.obliczamy wartość skręcalności molowej ze wzoru : Φ= *M/100, gdzie MC6H12O6 = 180g/mol
Φ=49,8386*180/100=89,70948
3,1 Obliczamy stężenie roztworu Cx otrzymanego do analizy ze wzoru:
Cx= φx/ *l gdzie φx = 1,97
Cx= 1,97/49,8386*1,85=0,0214
4 Wyznaczamy równanie regresji liniowej dla zależności kąta skręcania płaszczyzny polaryzacji światła od stężenia roztworu substancjii optycznie czynnej.
nr |
C=x |
y |
x-x |
(x-x)2 |
y-y |
(y-y)2 |
(x-x)(y-y) |
1 |
0,007 |
0,5985 |
-0,0315 |
0,00099225 |
-2,997646 |
8,985882 |
0,094426 |
2 |
0,014 |
1,24146 |
-0,0245 |
0,00060025 |
-2,354686 |
5,544546 |
0,05769 |
3 |
0,021 |
1,8981 |
-0,0175 |
0,00030625 |
-1,698046 |
2,88336 |
0,029716 |
4 |
0,028 |
2,7634 |
-0,0105 |
0,00011025 |
-0,832746 |
0,693466 |
0,008744 |
5 |
0,035 |
3,1635 |
-0,0035 |
0,00001225 |
-0,432646 |
0,187183 |
0,001514 |
6 |
0,042 |
3,8133 |
0,0035 |
0,00001225 |
0,217154 |
0,047156 |
0,00076 |
7 |
0,049 |
4,5144 |
0,0105 |
0,00011025 |
0,918254 |
0,84319 |
0,009642 |
8 |
0,056 |
5,3626 |
0,0175 |
0,00030625 |
1,766454 |
3,12036 |
0,030913 |
9 |
0,063 |
6,0295 |
0,0245 |
0,00060025 |
2,433354 |
5,921212 |
0,059617 |
10 |
0,07 |
6,5767 |
0,0315 |
0,00099225 |
2,980554 |
8,883702 |
0,093887 |
SUMA |
0,385 |
35,96146 |
|
0,0040425 |
|
37,11006 |
0,386909 |
X=0,0385Y=3,596146
a= Σ(x-x)(y-y)/ Σ(x-x)2 = 0,386909/0,0040425=95,710328
b= y-ax = 3,596146-95,710328*0,0385=-0,089
y=ax+b = 95,710328X-0,104255
Sxy = [Σ (y-y)2 -a2 Σ(x-x)2 /(n-2)]0,5 = [37,11006-(95,710328)2*0,0040425/8]0,5 = 0,099292881
5 Sprawdzamy hipotezę H0:b=0 na poziomie istotności α=0,05
5,1 odchylenie standardowe wyrazu wolnego
Sb=[1/n+x2 / Σ(x-x)2 ]0,5 *Sxy
Sb=[1/8-(0,0385)2/0,0040425]0,5 *0,099292881= 0,069623
5,2 obliczamy wielkość texp=|b|/Sb
texp=0,089/0,069623=1,27831
ttab(α=0,05;k=n-2=8)=2,31
Wnioski : texp=<ttab przyjmujemy hipotezę H0:b=0
6 Przedział ufności wartości CX
6,1 Stężenie roztworu obliczamy z przekształcenia wzoru X=y-b/a gdzie y=φX=1,97
X= CX = 1,97+0,089/95,710328=0,02153
6.2 obliczamy odchylenie standardowe SX
SX = Sxy /a [1+1/n+Σ (y-y)2 / a2 Σ(x-x)2 ]0,5 =0,099292881/95,710328 [1+1/10+37,11006 / (95,710328)2*0,0040425]0,5 =0,001037431*1,449872373=0,001504
6,3 Wartość t-Studenta dla α=0,05 i k=n-2=8
t=2,31
Sx*t=0,001504*2,31=0,003474
Analiza
X- Sx*t=0,02153-0,003474=0,018056
X+ Sx*t=0,02153+0,003474=0,025004
0,018056<μx< 0,025004
ZESTAWIENIE KOŃCOWE
|
C |
Sx |
X-S*t <μx< X+S*t |
1,97 |
0,02153 |
0,001504 |
0,018056<μx< 0,025004 |
![]()
![]()
Wyszukiwarka
Podobne podstrony:
15 Adsorpcja, 15.krzychu, Wydział
15 Adsorpcja, Ćwiczenie 15 ADSORPCJA, Ćwiczenie 15 ADSORPCJA
wyklad badania mediow 15 i 16
15 ROE
15 Sieć Następnej Generacjiid 16074 ppt
wyklad 15 chemiczne zanieczyszczenia wod 2
Wykład 1 15
15 Uklady PLL i t s
Ćwiczenia i seminarium 1 IV rok 2014 15 druk
15 Fizjologiczne funkcje nerek
więcej podobnych podstron