Macierze

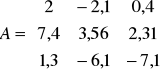
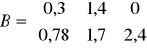
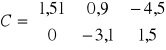
Na powyższych macierzach wykonaj następujące działania:

1. Dodawanie, tzn. A+B, A+C, B+C. Zastanów się które z tych działań są niemożliwe do wykonania i dlaczego? Sprawdź czy dodawanie macierzy jest przemienne?

2. Odejmowanie: A-B, A-C, B-C. Zastanów się które z tych działań są niemożliwe do wykonania i dlaczego? Sprawdź czy odejmowanie macierzy jest przemienne?

3. Mnożenie macierzy: A*B, A*C, B*C. Które z działań są niemożliwe do wykonania? Jakiego rodzaju przekształcenia np. macierzy „C” należałoby dokonać aby możliwe było wykonanie działania C*B? Wprowadź wektor „D” o takich wymiarach aby możliwe było wykonanie działania A*D. Wprowadź macierz jednostkową „I” o wymiarach 3 x 3 i pomnóż ją przez macierz „A”. W jakich przypadkach mnożenie macierzy jest przemienne?

4. Mnożenie macierzy przez liczbę. Pomnóż każdą z macierzy przez 1, 0, -1 oraz dowolnie wybraną wartość. Który z wyników można określić jako macierz przeciwną macierzy A? Która z macierzy wynikowych jest macierzą osobliwą?

5. Wprowadź taką macierz „E” aby prawdziwe było wyrażenie E = B.

6. Na których z powyższych macierzy możliwe jest wykonanie takich działań jak transponowanie i odwracanie? Wprowadź macierz symetryczną .

7. Z wykorzystaniem rachunku macierzowego rozwiąż poniższy układ równań i znajdź niewiadome x, y, z:

2x + 3,5y - z = 7

1,7x - 0,6y + 2z = 2

2,1x + 5z = 24

Schemat obliczeń:

Ułóż macierz S - wartości „stojących” przy niewiadomych oraz wektor W - wartości „wolnych”.

Wektor X jest poszukiwanym wektorem niewiadomych.

S*X = W

X = S ^-1*W

Obliczenia w programie MATLAB:

• Po uruchomieniu programu pojawi się okno z oznaczeniem:

<>

Przy tym znaczku należy wpisywać wszystkie macierze i działania na nich.

• Wprowadzanie macierzy, np. macierzy A

<>a=<2 -2.1 0.4;

7.4 3.56 2.31;

1.3 -6.1 -7.1> nacisnąć enter i pojawi się wprowadzona macierz

• Aby wykonywać działania na określonych macierzach można posługiwać się ich nazwami, tzn.:

<>a+b enter

<>a-b enter

<>a*b enter

<>a/b enter

• Jeśli macierz wynikowa ma mieć konkretną nazwę (nie dłuższą niż 4 znaki) należy ją wpisać przed działaniem:

<>e=a+b enter

<>f=a-b enter

<>g=a*b enter

<>h=a/b enter

• Aby przywołać określoną macierz wystarczy wpisać jej nazwę i nacisnąć enter. Przy nadawaniu nazw macierzom trzeba pamiętać aby nazwy się nie powtarzały, gdyż program bez ostrzeżenia zapamiętuje ostatnią nazwę.

• obliczanie wyznacznika macierzy A:

<> wma=det (a) enter

• odwracanie macierzy A:

<>moa=inv(a) enter

• transponowanie macierzy A:

<>mta=a'

Te same działania można wykonać w programie MsExcell:

Np. odwracanie macierzy:

• wpisujemy macierz (np. A):

• zaznaczamy obszar docelowy macierzy wynikowej,

• wchodzimy do funkcji (ikonka fx)i wybieramy „macierz.odw”

• w okienku „Tablica” zapisujemy zakres komórek, w którym mieszczą się wartości macierzy A,

• klikamy na pasku formuły i tam naciskamy jednocześnie klawisze „shift”, „ctrl” i „enter”

• w zaznaczonym obszarze (w tym przypadku w zakresie E2:G4) pojawi się wynik.

Analogicznie wykonywane są też inne działania na macierzach. Podstawą jest prawidłowe określenie zakresu komórek, w którym ma pojawić się wynik