Zadanie 48. (Całka oznaczona, definicje, własności, zastosowanie.)

DEFINICJA CAŁKI OZNACZONEJ

Wiemy (por. zadanie 47. o całce nieoznaczonej), że jeżeli F(x) jest funkcją pierwotną funkcji f(x) ciągłej w pewnym przedziale, to każda funkcja pierwotna funkcji f(x) w tym przedziale ma postać F(x) + C, gdzie C jest stałą. Wynika stąd, że różnica

F(x₂) - F(x₁)

w punktach x₂ i x₁ rozpatrywanego obszaru jest taka sama dla każdej funkcji pierwotnej F funkcji f. Różnicę tę nazywamy całką oznaczoną funkcji f od x₁ do x₂ i oznaczamy symbolem

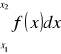
[A]

Mamy więc dla każdej funkcji f ciągłej w przedziale
:

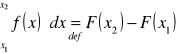
[B]

co zapisujemy także

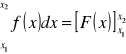
lub

i czytamy: całka oznaczona funkcji f(x) dx w granicach od x₁ do x₂ równa się F(x) z podstawieniem górnym x₂ i dolnym x_i.

Dokładna definicja całki oznaczonej jest bardziej rozbudowana:

Weźmy pod uwagę funkcję f(x), o której będziemy stale zakładali, że jest ograniczona w przedziale domkniętym
, tzn. dla
.

Dokonajmy różnych podziałów P₁, P₂,..., P_m­, ... przedziału
na części. Niech podział P_m będzie osiągnięty przy pomocy n_m - 1 liczb
, przy czym

,

gdzie dla ułatwienia oznaczyliśmy liczbę a jako
, a liczbę b jako
. Będziemy nazywali przedziały
, gdzie
, przedziałami cząstkowymi podziału
, a ich długości
oznaczali przez
. Niech
oznacza największą z liczb
, czyli długość najdłuższego przedziału cząstkowego podziału
. Ciąg podziałów
nazywamy normalnym ciągiem podziałów, jeżeli
.

Utwórzmy sumę
iloczynów wartości funkcji
w dowolnym punkcie
przedziału
przez długości
tych przedziałów przy podziale
:

[C]

Jeżeli ciąg
dla
jest zbieżny i do tej samej granicy przy każdym normalnym ciągu podziałów
niezależnie od wyboru punktów
, to funkcję
nazywamy funkcją całkowalną w przedziale
, a granicę ciągu [C] nazywamy całką oznaczoną funkcji
w granicach od a do b i oznaczamy symbolem

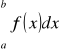
[D]

Można wykazać, że jeżeli przy jakimś ciągu normalnym podziałów ciąg
ma granicę niezależną od wyboru punktów
, to funkcja
jest całkowalna.

Jednym z prostych sposobów tworzenia ciągu normalnego podziałów jest kolejne przepoławianie przedziałów cząstkowych; wówczas

,
.

Można również wykazać, że funkcja ciągła w przedziale domkniętym jest całkowalna, a nawet ogólniej, że funkcja ograniczona w przedziale domkniętym oraz ciągła w nim z wyjątkiem co najwyżej skończonej liczby punktów jest całkowalna.

INTERPRETACJA GEOMETRYCZNA CAŁKI OZNACZONEJ

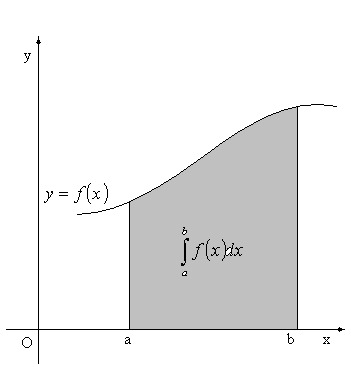
Jeżeli w przedziale
jest
, to pole obszaru ograniczonego łukiem krzywej
, odcinkiem osi Ox oraz prostymi x = a i
x = b równa się całce oznaczonej

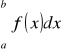
Jeżeli zaś w przedziale
jest
, to analogiczne pole równa się

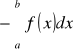
Zawsze więc pole wyżej określonego obszaru można wyrazić całką oznaczoną

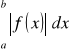
Przez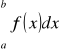
, gdzie a > b, rozumiemy całkę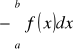
.

Przyjmujemy również, że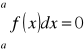

WŁASNOŚCI CAŁKI OZNACZONEJ

1. Addytywność całek oznaczonych względem przedziału całkowania.

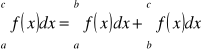
[E]

2. Stały czynnik można wyłączyć przed znak całki oznaczonej.

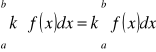
[F]

W szczególności, gdy k = -1

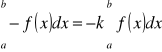
3. Całka sumy równa się sumie całek.

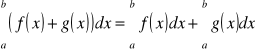
[G]

Jest to tzw. addytywność całki względem funkcji podcałkowej.

Całka oznaczona posiada więc własność tzw. liniowości ( własność 2. i 3.). Wzory powyższe należy rozumieć w ten sposób, że z istnienia całek po prawej stronie wynika istnienie całki po lewej stronie oraz podana równość.

4. Prawdziwy jest wzór:

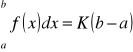
[H]

gdzie K jest pewną liczbą, spełniającą nierówność
, przy czym m oznacza kres dolny, a M kres górny funkcji f(x) w przedziale
.

Na podstawie własności Darboux mówiącej, że funkcja ciągła przybiera wszystkie wartości pośrednie między swymi kresami górnym i dolnym, wzór ten może przyjąć postać

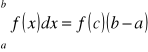
[I]

gdzie c jest pewną liczbą, spełniającą nierówność
, jeżeli funkcja podcałkowa f(x) jest ciągła w przedziale
.

5. Całka jako funkcja górnej granicy.

Jeżeli funkcja f(t) jest ciągła w przedziale
, to funkcja

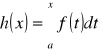
[J]

jest ciągła i różniczkowalna względem zmiennej x w przedziale
i w każdym punkcie tego przedziału zachodzi związek

[K]

6. Związek między całką oznaczoną a nieoznaczoną.

Jeżeli przez F(x) oznaczymy funkcję pierwotną funkcji f(x), ciągłej w przedziale
, tzn. jeżeli
, to ma miejsce wzór

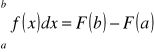
, [L]

przy czym oczywiście różnica
nie zależy od stałej całkowania C.
Wzór [L] nazywamy wzorem Leibniza-Newtona.

Uwaga. Prawą stronę powyższego wzoru oznacza się symbolem

lub
[M]

7. Całkowanie przez części dla całek oznaczonych.

Jeżeli u, v są funkcjami zmiennej x mającymi ciągłą pochodną, to

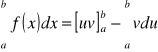
[N]

Jest to wzór na całkowanie przez części dla całek oznaczonych.

8. Całkowanie przez podstawienie dla całek oznaczonych.

Jeżeli g'(x) jest funkcją ciągłą, g(x) funkcją rosnącą w przedziale
, a f(u) funkcją ciągłą w przedziale
, to zachodzi następujący wzór:

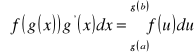
[O]

Jest to wzór na całkowanie przez podstawienie dla całek oznaczonych.

9. Jeżeli funkcja g różni się od funkcji h, całkowalnej na odcinku
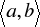
   , tylko dla skończenie wielu argumentów z tego przedziału, to funkcja g również jest całkowalna i

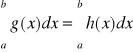
[P]

Wnioski:

1°. Funkcja nieciągła tylko dla skończenie wielu punktów przedziału
i ograniczona w tym przedziale jest na nim całkowalna.

2°. Dla całkowalności funkcji ograniczonej w przedziale nie są istotne ani jej wartości, ani nawet określoność w końcach tego przedziału.

3°. Funkcja nieograniczona nie jest całkowalna (uwaga ta nie dotyczy tzw. całki niewłaściwej).

10. Znajdowanie długości łuku krzywej
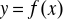
    w przedziale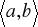
    .

długość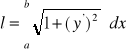
gdzie
[R]

Dla krzywej danej w postaci parametrycznej x = x(t), y = y(t),
mamy:

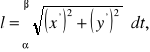
gdzie

[S]

Interpretacja fizyczna:

1°. Wiemy, że prędkość v(t) punktu P poruszającego się po osi OS jest pochodną drogi s(t) względem czasu t.

Droga S(t) jest więc funkcją pierwotną prędkości; stąd

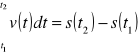
2°. Praca jako całka siły. Niech f(s) oznacza miarę na osi OS wektora siły działającej na masę umieszczoną w punkcie o współrzędnej s. Praca wykonana przez tę siłę na przesunięcie masy z położenia
w położenie
, równa jest całce funkcji f(s) od
do
.

praca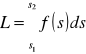

Przykład 1.

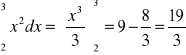
Odp.
.

Przykład 2.

Obliczyć pole ograniczone łukiem cosinusoidy y = cos x od
do
i osią Ox.

pole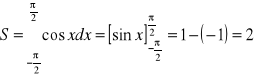

Odp. 2.

Przykład 3.

Obliczyć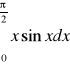
.

Rozwiązanie: Stosujemy wzór [N] na całkowanie przez części i otrzymujemy

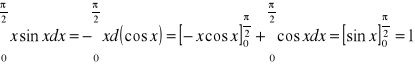
Odp. 1.

Przykład 4.

Obliczyć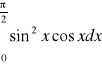
.

Rozwiązanie: Stosując wzór [O] na całkowanie przez podstawienie i przyjmując sin x = u

otrzymujemy

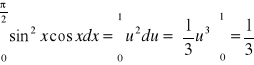
Odp.
.

Uwaga: Przykłady 3 i 4 można też rozwiązać obliczając najpierw całki nieoznaczone, a następnie skorzystać ze związku [L].

Przykład 5.

Obliczyć pole ograniczone liniami:

oraz y = x

Rozwiązanie: Sporządzamy rysunek

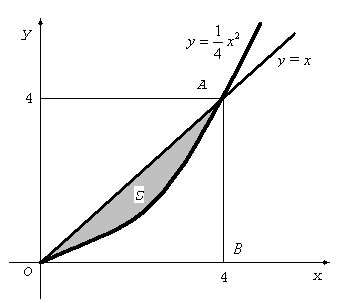
Szukane pole S jest różnicą 2 pól: trójkąta OAB i figury ograniczonej osią Ox, prostą x = 4 i krzywą
. Stąd

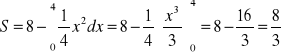
Odp.
.

Przykład 6.

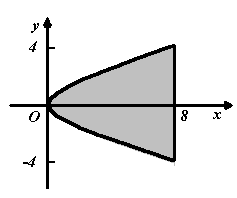
Obliczyć pole ograniczone łukiem paraboli
oraz prostą x = 8.

Rozwiązanie: Ze względu na symetrię paraboli
względem osi Ox wystarczy obliczyć pole ograniczone osią Ox, prostą x = 8 i łukiem paraboli w pierwszej ćwiartce i otrzymany wynik podwoić.

Obliczamy całkę oznaczoną

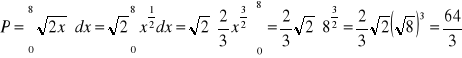
Odp.: Poszukiwane pole wynosi
.

Opracował: Jakub Marszałkiewicz IVa.

8

---