KATEDRA PODSTAW KONSTRUKCJI MASZYN

PRACA KONTROLNA Nr1

Kozłowski Krzysztof

MD 103.6b

Wałek (szkic) wykonany ze stali 45 o szlifowanej powierzchni przenosi moment zginający Mg = 650 Nm o współczynniku stałości obciążenia κg = 0,5

i jednocześnie moment skręcający Ms = 150 Nm, dla którego współczynnik stałości obciążenia κs = 0.

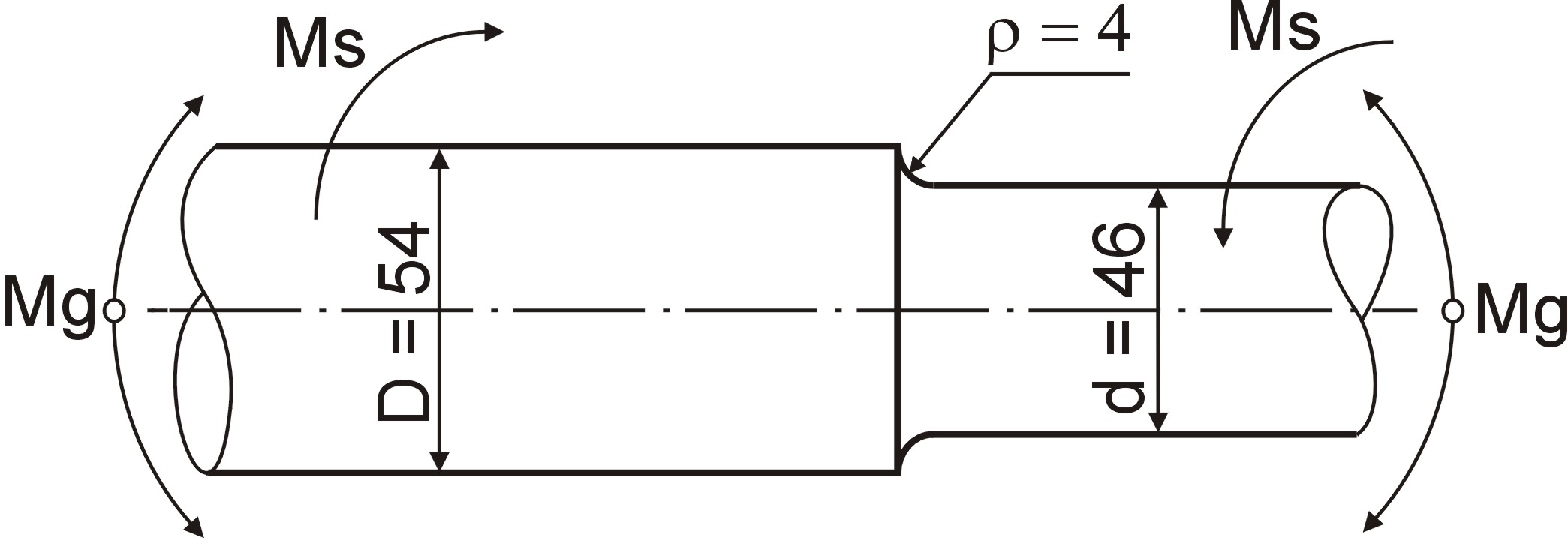
Obliczyć rzeczywisty współczynnik bezpieczeństwa δ.

1. Dane.

Moment zginający:

Mg = 650 Nm

Współczynnik stałości obciążenia κ:

κg = 0,5.

Moment skręcający:

Ms = 150 Nm

Współczynnik stałości obciążenia κ:

κs = 0.

Materiał wałka:

Stal 45.

stal	Własności wytrzymałościowe [N/mm^2]
		Rm		Re	Zrj	Zgj	Zsj	Zrc	Zgo	Zso
		min	max
45	660	800	410	410	555	365	230	310	183

2. Obliczenia.

1. Rzeczywisty współczynnik bezpieczeństwa δ dla jednoczesnego zginania i skręcania wyliczam ze wzoru:

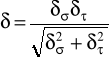
gdzie:

δ_τ - rzeczywisty współczynnik bezpieczeństwa dla skręcania

δ_σ- rzeczywisty współczynnik bezpieczeństwa dla zginania

• Wyliczam rzeczywisty współczynnik bezpieczeństwa dla zginania w cyklu dwustronnym δ_σ:

gdzie:

Z_go - wytrzymałość na zginanie obustronne,

β - współczynnik spiętrzenia naprężeń,

σ_na - nominalna amplituda naprężeń zginających,

σ_m - naprężenia średnie,

ψ - współczynnik wrażliwości materiału na asymetrię cyklu,

- współczynnik wielkości przedmiotu.

• Wytrzymałość na zginanie obustronne - Z_go

Z_go = 310

• Obliczam współczynnik spiętrzenia naprężeń zginających - β:

β = β_k + β_p - 1

gdzie:

β_k - współczynnik działania karbu,

β_p - współczynnik stanu powierzchni.

Aby odczytać z wykresu wartość β_k muszę znać wartość

współczynnika kształtu α_k, R_m materiału i ρ.

α_k wyznacza się z wykresu znając wartości stosunków
i
.

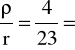
0,1739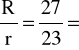
1,1739

współczynnik kształtu α_k = 1,67

(wg wykresu II - 10)

ρ = 4

R_m = 750

współczynnik działania karbu β_k = 1,59

(wg wykresu II - 19)

współczynnik wrażliwości na działanie karbu η_k = 0,88

(wg wykresu II - 19)

Aby odczytać z wykresu wartość β_p muszę znać wartość R_m i rodzaj obróbki materiału.

dla R_m = 750
i powierzchni szlifowanej:

β_p = 1,1

(wg wykresu II - 21)

Współczynnik spiętrzenia naprężeń - β:

β = β_k + β_p - 1

β = 1,59 + 1,1 - 1

β = 1,69

• Obliczam σ_na - nominalną amplitudę naprężeń zginających,

oraz σ_m - naprężenia średnie.

Naprężenia średnie σ_m są równe:

Nominalna amplituda naprężeń zginających σ_na jest równa:

gdzie:

σ_max - naprężenia maksymalne,

σ_min - naprężenia minimalne.

Naprężenia maksymalne σ_max są równe:

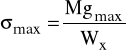
gdzie:

Mg_max - maksymalny moment gnący,

W_x - wskaźnik wytrzymałości przekroju na zginanie,

dla koła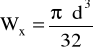

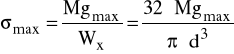
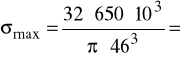
68,02

naprężenia maksymalne - σ_max = 68,02

Naprężenia minimalne σ_min są równe:

gdzie:

R - współczynnik amplitudy cyklu.

Współczynnik amplitudy cyklu - R jest równy:

gdzie:

κ - współczynnik asymetrii cyklu.

κ = 0,5

więc naprężenia minimalne σ_min są równe:

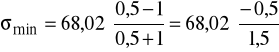
22,67

Naprężenia minimalne σ_min = -22,67
.

Naprężenia średnie σ_m są równe:

σ_m = 22,67
.

Nominalna amplituda naprężeń zginających σ_na jest równa:

σ_na = 45,35
.

• współczynnik wrażliwości materiału na asymetrię cyklu - ψ:

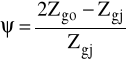
gdzie:

Z_go - wytrzymałość na skręcanie obustronne,

Z_gj - wytrzymałość na skręcanie jednostronne.

Wytrzymałość na skręcanie obustronne - Z_go:

Z_go= 310

Wytrzymałość na skręcanie jednostronne - Z_gj:

Z_gj = 555

ψ = 0,117

• Współczynnik wielkości przedmiotu - γ:

Wartość γ odczytuje się z wykresu z wykresu znając wartości Z_go,α_k i d

Z_go = 310

α_k = 1,67

d = 46 mm

Współczynnik wielkości przedmiotu - γ = 1,34.

(wg wykresu II - 23)

Rzeczywisty współczynnik bezpieczeństwa dla zginania w cyklu

dwustronnym δ_σ:

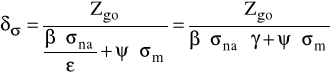
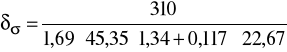
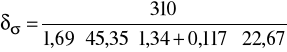
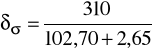
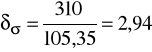
δ_σ = 2,94

• Wyliczam rzeczywisty współczynnik bezpieczeństwa dla skręcania w

cyklu wahadłowym δ_τ:

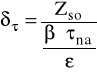
(wg Serensena)

gdzie:

τ_na - naprężenia skręcające amplitudowe,

β - współczynnik spiętrzenia naprężeń skręcających,

- współczynnik wielkości przedmiotu.

• Naprężenia skręcające amplitudowe - τ_na, są równe naprężeniom

maksymalnym - τ_max.

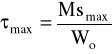
gdzie:

Mg _max - maksymalny moment skręcający,

W_o - wskaźnik wytrzymałości przekroju na skręcanie.

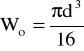
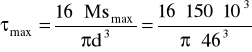
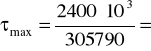
7,85

• Obliczam współczynnik spiętrzenia naprężeń skręcających - β:

β = β_k + β_p - 1

gdzie:

β_k - współczynnik działania karbu,

β_p - współczynnik stanu powierzchni.

Aby odczytać z wykresu wartość β_k muszę znać wartość

współczynnika kształtu α_k, R_m materiału i ρ.

α_k wyznacza się z wykresu znając wartości stosunków
i
.

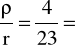
0,1739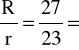
1,1739

współczynnik kształtu α_k = 1,40

(wg wykresu II - 14)

ρ = 4

R_m = 750

współczynnik działania karbu β_k = 1,35

(wg wykresu II - 19)

współczynnik wrażliwości na działanie karbu η_k = 0,88

(wg wykresu II - 19)

Aby odczytać z wykresu wartość β_p muszę znać wartość R_m i rodzaj

obróbki materiału:

dla R_m = 750
i powierzchni szlifowanej:

β_p = 1,1

(wg wykresu II - 21)

Współczynnik spiętrzenia naprężeń - β:

β = β_k + β_p - 1

β = 1,35 + 1,1 - 1

β = 1,45

• Współczynnik wielkości przedmiotu - γ.

Wartość γ odczytuje się z wykresu z wykresu znając wartości Z_go,

α_k i d

Z_go = 310

α_k = 1,40

d = 46 mm

Współczynnik wielkości przedmiotu - γ = 1,28.

(wg wykresu II - 23)

Wyliczam rzeczywisty współczynnik bezpieczeństwa dla skręcania w

cyklu odzerowo-tętniącym δ_τ:

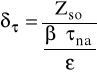
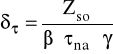
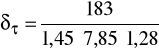
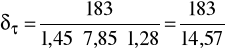
δ_τ = 12,56

Rzeczywisty współczynnik bezpieczeństwa δ dla jednoczesnego zginania

i skręcania wyliczam ze wzoru:

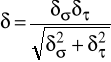
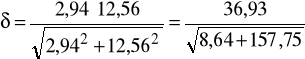
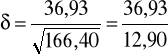
δ = 2,86

3. Wnioski.

Ustalona dzięki obliczeniom wartość rzeczywistego współczynnika bezpieczeństwa - δ = 2,86 jest zbyt duża, gdyż przekracza nawet wartość stosowaną w obliczeniach orientacyjnych - δ ∈(2,2 ÷ 2,5).

Dlatego wartość rzeczywistego współczynnika bezpieczeństwa można z powodzeniem obniżyć do poziomu wartości stosowanej najczęściej - δ ∈(1,5 ÷ 1,7), aby tego dokonać można:

• Zastosować gorszej jakości materiał,

• Zastosować gorszej jakości obróbkę,

• Zwiększyć obciążenia wałka.

4. Literatura.

1.Dietrych, Kocańda, Korewa - Podstawy konstrukcji maszyn, część I.

WNT. Warszawa 1974

2.Opracowanie zbiorowe - Przykłady obliczeń z podstaw konstrukcji

maszyn, część I. Wydawnictwa Uczelniane. Lublin 1997

---