2.2.1 Ściana wewnętrzna nośna

III kondygnacji :

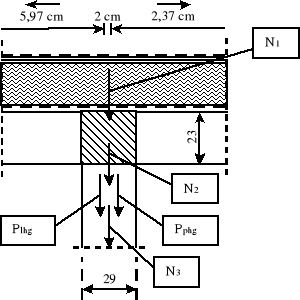
P_phg siła od reakcji ze stropodachu z prawej :

gdzie : N_vg -siła działająca do połowy wysokości ściany,

e_vg -mimośród siły N_vg,

P_l/phg -siła od stropodachu z lewej i prawej strony,

e_l/phg -mimośród siły P_l/phg z lewej i prawej strony.

gdzie : N_vd -siła działająca na całą wysokość ściany,

e_vd -mimośród siły N_vd,

gdzie : e_s -mimośród siły podłużnej otrzymanej z obliczeń statycznych,

e_g -mimośród siły podłużnej działającej z góry,

e_d -mimośród siły podłużnej działającej z dołu.

gdzie :

e_n -mimośród przypadkowy,

e₀ -mimośród początkowy.

Wysokość kondygnacji obliczamy wg wzoru :

gdzie :χ_v -wsp. wyrażający wpływ usztywnienia muru wzdłuż krawędzi pionowych,

χ_h -wsp. wyrażający wpływ usztywnienia muru wzdłuż krawędzi poziomych,

l_k -wysokość kondygnacji w świetle.

l₀ -wysokość obliczeniowa kondygnacji w świetle.

Sprawdzenie stosunku oraz w celu odczytania wartości współczynnika wyrażającego wpływ mimośrodu, smukłości i obciążeń długotrwałych na nośność elementu.

gdzie : l₀ -wysokość obliczeniowa kondygnacji w świetle,

e₀ -mimośród początkowy,

h -wysokość przekroju poprzecznego obliczanego

muru.

Na podstawie tablicy 5 odczytano wartość współczynnika ϕ=0,77

Obliczenie wytrzymałości muru niezbrojonego na ściskanie R_m które obliczamy wg wzoru :

gdzie :

R_mk -charakterystyczna wytrzymałość na ściskanie muru niezbrojonego zależna od wytrzymałości średniej pustaka na ściskanie i wytrzymałości zaprawy na ściskanie,

m_m -współczynnik korekcyjny,

γ_m1, γ_m -współczynniki materiałowe dla muru.

Przyjęto wytrzymałość pustaków na ściskanie równą 15MPa, oraz markę zaprawy 3, wtedy

R_mk=2,8 MPa oraz R_m. Na tej podstawie określono również cechę sprężystości muru α_m.=1000.

Nośność muru na ściskanie obliczamy wg wzoru :

gdzie :R_m -wytrzymałość obliczeniowa muru na ściskanie,

F_m -pole poprzeczne muru,

• -współczynnik korekcyjny.

NOŚNOŚĆ ZACHOWANA *

2.2.2. Ściana wewnętrzna nośna

II kondygnacji :

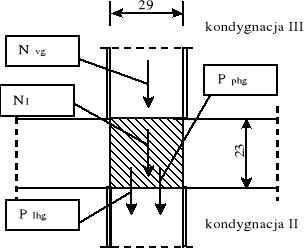
P_lhg -siła od reakcji ze stropu z lewej strony :

P_phg siła od reakcji ze stropu z prawej :

gdzie :

R− reakcja obliczeniowa od stropu,

a− rozstaw belek stropu Fert-40

gdzie : N*_vg -siła działająca do połowy wysokości ściany,

e_vg -mimośród siły N*_vg,

P_l/phg -siła od stropu z lewej i prawej strony,

e_l/phg -mimośród siły P_l/phg z lewej i prawej strony.

gdzie : N_vd -siła działająca na całą wysokość ściany,

e_vd -mimośród siły N_vd,

gdzie : e_s -mimośród siły podłużnej otrzymanej z obliczeń statycznych

e_g -mimośród siły podłużnej działającej z góry

e_d -mimośród siły podłużnej działającej z dołu

gdzie :

e_n -mimośród przypadkowy

e₀ -mimośród początkowy

Wysokość kondygnacji obliczamy wg wzoru :

gdzie :χ_v -wsp. wyrażający wpływ usztywnienia muru wzdłuż krawędzi pionowych,

χ_h -wsp. wyrażający wpływ usztywnienia muru wzdłuż krawędzi poziomych,

l_k -wysokość kondygnacji w świetle.

l₀ -wysokość obliczeniowa kondygnacji w świetle.

Sprawdzenie stosunku oraz w celu odczytania wartości współczynnika wyrażającego wpływ mimośrodu, smukłości i obciążeń długotrwałych na nośność elementu.

gdzie : l₀ -wysokość obliczeniowa kondygnacji w świetle,

e₀ -mimośród początkowy,

h -wysokość przekroju poprzecznego obliczanego

muru.

Na podstawie tablicy 5 odczytano wartość współczynnika ϕ=0,85

Obliczenie wytrzymałości muru niezbrojonego na ściskanie R_m które obliczamy wg wzoru :

gdzie :

R_mk -charakterystyczna wytrzymałość na ściskanie muru niezbrojonego zależna od wytrzymałości średniej pustaka na ściskanie i wytrzymałości zaprawy na ściskanie,

m_m -współczynnik korekcyjny,

γ_m1., γ_m -współczynniki materiałowe dla muru.

Przyjęto wytrzymałość pustaków na ściskanie równą 15MPa, oraz markę zaprawy 3, wtedy

R_mk=2,8 MPa oraz R_m. Na tej podstawie określono również cechę sprężystości muru α_m.=1000.

Nośność muru na ściskanie obliczamy wg wzoru :

gdzie :R_m -wytrzymałość obliczeniowa muru na ściskanie,

F_m -pole poprzeczne muru,

• -współczynnik korekcyjny.

NOŚNOŚĆ ZACHOWANA *

Ściana wewnętrzna nośna

I kondygnacji :

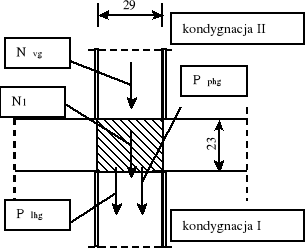
P_lhg -siła od reakcji ze stropu z lewej strony :

P_phg siła od reakcji ze stropu z prawej :

gdzie : R- reakcja obliczeniowa od stropu (poz.1.2.4)

a- rozstaw belek stropu Fert-40

gdzie : N**_vg -siła działająca do połowy wysokości ściany,

e_vg -mimośród siły N**_vg,

P_l/phg -siła od stropu z lewej i prawej strony,

e_l/phg -mimośród siły P_l/phg z lewej i prawej strony.

gdzie : N_vd -siła działająca na całą wysokość ściany,

e_vd -mimośród siły N_vd,

gdzie : e_s -mimośród siły podłużnej otrzymanej z obliczeń statycznych,

e_g -mimośród siły podłużnej działającej z góry,

e_d -mimośród siły podłużnej działającej z dołu.

gdzie :

e_n -mimośród przypadkowy,

e₀ -mimośród początkowy.

Wysokość kondygnacji obliczamy wg wzoru :

gdzie :χ_v -wsp. wyrażający wpływ usztywnienia muru wzdłuż krawędzi pionowych,

χ_h -wsp. wyrażający wpływ usztywnienia muru wzdłuż krawędzi poziomych,

l_k -wysokość kondygnacji w świetle,

l₀ -wysokość obliczeniowa kondygnacji w świetle.

Sprawdzenie stosunku oraz w celu odczytania wartości współczynnika wyrażającego wpływ mimośrodu, smukłości i obciążeń długotrwałych na nośność elementu.

gdzie : l₀ -wysokość obliczeniowa kondygnacji w świetle,

e₀ -mimośród początkowy,

h -wysokość przekroju poprzecznego obliczanego

muru.

Na podstawie tablicy 5 odczytano wartość współczynnika ϕ=0,82

Obliczenie wytrzymałości muru niezbrojonego na ściskanie R_m które obliczamy wg wzoru :

gdzie :

R_mk -charakterystyczna wytrzymałość na ściskanie muru niezbrojonego zależna od wytrzymałości średniej pustaka na ściskanie i wytrzymałości zaprawy na ściskanie,

m_m -współczynnik korekcyjny,

γ_m1., γ_m -współczynniki materiałowe dla muru.

Przyjęto wytrzymałość pustaków na ściskanie równą 15MPa, oraz markę zaprawy 3, wtedy

R_mk=2,8 MPa oraz R_m. Na tej podstawie określono również cechę sprężystości muru α_m.=1000.

Nośność muru na ściskanie obliczamy wg wzoru :

gdzie :R_m -wytrzymałość obliczeniowa muru na ściskanie,

F_m -pole poprzeczne muru,

• -współczynnik korekcyjny.

NOŚNOŚĆ ZACHOWANA *

2.2.4 Ściana wewnętrzna nośna

piwnicy :

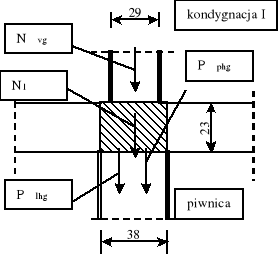
P_lhg -siła od reakcji ze stropu z lewej strony :

gdzie :

P_phg siła od reakcji ze stropu z prawej :

R− reakcja obliczeniowa od stropu,

a− rozstaw belek stropu Fert-40.

gdzie : N***_vg -siła działająca do połowy wysokości ściany,

e_vg -mimośród siły N***_vg,

P_l/phg -siła od stropu z lewej i prawej strony,

e_l/phg -mimośród siły P_l/phg z lewej i prawej strony.

gdzie : N_vd -siła działająca na całą wysokość ściany,

e_vd -mimośród siły N_vd,

gdzie : e_s -mimośród siły podłużnej otrzymanej z obliczeń statycznych,

e_g -mimośród siły podłużnej działającej z góry,

e_d -mimośród siły podłużnej działającej z dołu.

gdzie :

e_n -mimośród przypadkowy,

e₀ -mimośród początkowy.

Wysokość kondygnacji obliczamy wg wzoru :

gdzie :χ_v -wsp. wyrażający wpływ usztywnienia muru wzdłuż krawędzi pionowych,

χ_h -wsp. wyrażający wpływ usztywnienia muru wzdłuż krawędzi poziomych,

l_k -wysokość kondygnacji w świetle.

l₀ -wysokość obliczeniowa kondygnacji w świetle.

Sprawdzenie stosunku oraz w celu odczytania wartości współczynnika wyrażającego wpływ mimośrodu, smukłości i obciążeń długotrwałych na nośność elementu.

gdzie : l₀ -wysokość obliczeniowa kondygnacji w świetle,

e₀ -mimośród początkowy,

h -wysokość przekroju poprzecznego obliczanego

muru.

Na podstawie tablicy 5 odczytano wartość współczynnika ϕ=0,855

Obliczenie wytrzymałości muru niezbrojonego na ściskanie R_m które obliczamy wg wzoru :

gdzie :

R_mk -charakterystyczna wytrzymałość na ściskanie muru niezbrojonego zależna od wytrzymałości średniej pustaka na ściskanie i wytrzymałości zaprawy na ściskanie,

m_m -współczynnik korekcyjny,

γ_m1., γ_m -współczynniki materiałowe dla muru.

Przyjęto wytrzymałość pustaków na ściskanie równą 15MPa, oraz markę zaprawy 3, wtedy

R_mk=2,8 MPa oraz R_m. Na tej podstawie określono również cechę sprężystości muru α_m.=1000.

Nośność muru na ściskanie obliczamy wg wzoru :

gdzie :R_m -wytrzymałość obliczeniowa muru na ściskanie,

F_m -pole poprzeczne muru,

• -współczynnik korekcyjny.

NOŚNOŚĆ ZACHOWANA *

---