Współczesne układy sterowania

Tematy wykładów

1. Wstęp. Podstawowe pojęcia. Klasyfikacja układów sterowania. Regulatory liniowe i nieliniowe. Regulatory PID. Korektory wyprzedzająco-opóźniające. Projektowanie układów metodami klasycznymi.

2. Opis układu w przestrzeni stanów. Sterowalność, stabilizowalność. Projektowanie układu metodą sprzężenia od stanu.

3. Obserwowalność. Projektowanie obserwatora stanu. Projektowanie układu regulacji ze sprzężeniem od stanu obserwowanego. Zasada separowalności estymacji stanu i sterowania.

4. Obserwator rzędu zredukowanego.

5. Próbkowanie sygnału ciągłego. Równania różnicowe. Transmitancja dyskretna. Stabilność układów dyskretnych. Ekstrapolator rzędu zerowego. Regulacja cyfrowa.

6. Projektowanie układów sterowania optymalnego przy kwadratowym wskaźniku jakości. Równania stanu sprzężonego. Zasada maksimum. Równanie Riccatiego. Detektowalność systemu.

7. Projektowanie optymalnego obserwatora stanu − filtr Kalmana. Sterowanie optymalne systemu liniowego w przypadku zakłóceń gaussowskich.

Literatura

1. A. Niederliński. Systemy komputerowe automatyki przemysłowej. t. 2, WNT, 1985.

2. Ackerman. Regulacja impulsowa, WNT,1976.

3. Mańczak, Z. Nahorski. Komputerowa identyfikacja obiektów dynamicznych, PWN, 1983.

4. R. Yager, D. P. Filev. podstawy modelowania i sterowania rozmytego, WNT, 1995.

5. Osowski. Sieci neuronowe w ujęciu algorytmicznym, WNT, 1996.

6. Błachuta (red.). Laboratorium teorii sterowania i podstaw automatyki, Wyd. Pol. Śląskiej, 1998.

1. Wstęp

Podstawowe pojęcia

Klasyfikacja układów sterowania

Regulatory liniowe i nieliniowe. Regulatory PID

Korektory wyprzedzająco-opóŹniające

Projektowanie układów metodami klasycznymi

Klasyfikacja układów sterowania

Rys. 1. Otwarty układ sterowania

Rys. 2. Zamknięty układ sterowania − układ regulacji automatycznej

Rys. 3. Układ automatycznej kompensacjiRegulatory liniowe i nieliniowe

• regulatory nieliniowe: dwupołożeniowy, trójpołożeniowy,

• regulatory liniowe: PID, korektor wyprzedzająco-opóźniający.

Regulator PID − idealny

P I D

(1.1)

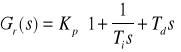
(1.2)

Dobór nastaw regulatora PID:

• metoda Zieglera-Nicholsa (metoda testu granicy stabilności)

, (1.3)

, (1.4)

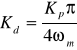
, (1.5)

− wzmocnienie krytyczne,

− pulsacja drgań nietłumionych.

• metoda testu odpowiedzi skokowej

Uproszczony model obiektu inercyjnego wysokiego rzędu

, (1.6)

− współczynnik wzmocnienia,

− czas martwy (opóźnienia),

− stała czasowa.

Nastawy regulatora oblicza się na podstawie parametrów modelu uproszczonego korzystając z tabel − (Poradnik inżyniera. Automatyka, str. 618-619).

Korektor wyprzedzająco-opóŹniający

(1.7)

- korektor wyprzedzający (ang. lead),

- korektor wyprzedzający (ang. lag).

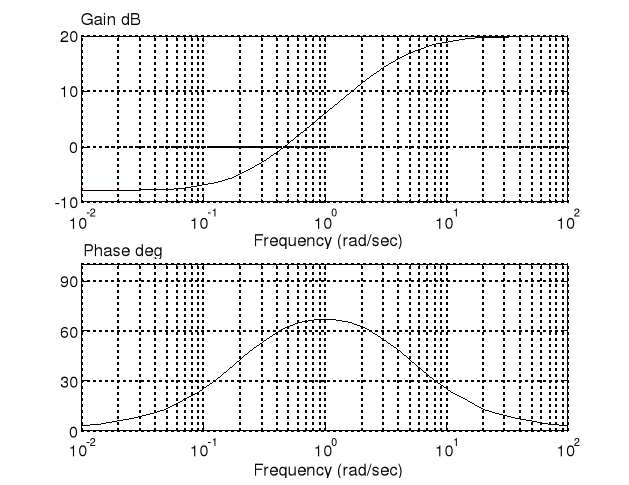
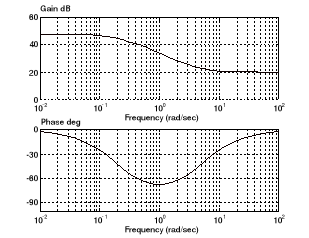
Rys. 4. Charakterystyki amplitudowo-fazowe korektora wyprzedzającego

Rys. 5. Charakterystyki amplitudowo-fazowe korektora opóźniającego

Maksymalne przesunięcie fazowe dla
.

Korektor wyprzedzający:

• zwiększa zapas stabilności układu zamkniętego,

• zwiększa uchyb statyczny,

• zmniejsza czas regulacji,

• zwiększa szerokość pasma przenoszenia (może być to niekorzystne ze względu na zwiększony wpływ szumów).

Korektor opóźniający:

• zmniejsza zapas stabilności układu zamkniętego (nie należy stosować dla obiektów niesta-bilnych lub o małym zapasie stabilności),

• zmniejsza uchyb statyczny,

• zwiększa czas regulacji,

• zmniejsza szerokość pasma przenoszenia (może być to korzystne ze względu na zmniej-szony wpływ szumów).

Projektowanie układów regulacji: metoda przemieszczania biegunów układu zamkniętego poprzez dodanie dodatkowych zer i biegunów do transmitancji układu otwartego - odpowiednie kształtowanie wykresu linii pierwiastkowych.

2. Projektowanie układów regulacji przy wykorzystaniu opisu w przestrzeni stanów

Idea metod: Przebiegi przejściowe w układach regulacji są zależne od położenia biegunów układu zamkniętego. Zadanie regulatora polega na takim przemieszczeniu biegunów, aby otrzymać pożądane właściwości układu zamkniętego.

Projektowanie układów regulacji metodą sprzężenia od stanu

Przykład 1. Dany jest niestabilny obiekt regulacji rzędu II opisany równaniami stanu

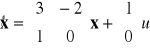
Bieguny układu otwartego można obliczyć rozwiązując równanie charakterystyczne układu

(2.1)

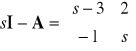
W układach ze sprzężeniem od stanu zakłada się, że sterowanie jest proporcjonalne do wektora stanu. Reguła sterowania ma następującą postać:

(2.2)

Zadanie polega na takim dobraniu wektora wzmocnień k, aby układ zamknięty był stabilny. Dla układu II-ego rzędu o jednym wejściu u

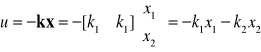
Równanie stanu układu zamkniętego

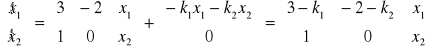
Równanie charakterystyczne układu zamkniętego

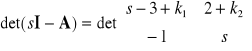
Załóżmy, że zadane jest położenie biegunów układu zamkniętego

Zadane równanie charakterystyczne układu zamkniętego ma postać:

Porównując zadane równanie charakterystyczne z równaniem charakterystycznym układu ze sprzężeniem od stanu otrzymujemy

Stąd wzmocnienia
i

Stosując powyższe zasady można przenosić bieguny układu w dowolne położenie w lewej półpłaszczyźnie zespolonej dobierając odpowiednio wartości wzmocnień
i
.

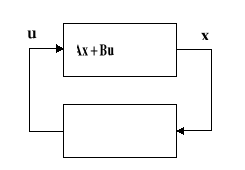
Rys. 6. Regulacja w układzie ze sprzężeniem od stanu

Metodę tą można stosować jedynie dla systemów, które spełniają warunek sterowalności.

Liniowy system dynamiczny jest sterowalny ⇔ jeżeli rząd macierzy sterowalności S jest równy rzędowi systemu n (wymiarowi wektora stanu).

(2.3)

Jeżeli system jest sterowalny, to stosując sprzężenie od stanu można ulokować bieguny w dowolnym miejscu na płaszczyźnie zespolonej.

W praktyce wystarcza spełnienie słabszego warunku stabilizowalności.

Liniowy system dynamiczny jest stabilizowalny, jeżeli jego niestabilne bieguny są sterowalne.

Przykład 2. Dany jest niestabilny system dynamiczny

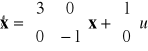
Równanie charakterystyczne systemu ma postać:

System ma jeden biegun niestabilny (+3). Macierz sterowalności:

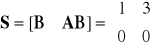
Rząd macierzy S jest równy 1. System ten nie jest więc sterowalny. Jednakże, niestabilny biegun systemu jest sterowalny, ponieważ za pomocą sprzężenia zwrotnego można zmienić jego położenie. Sygnał sterujący u określa zależność:

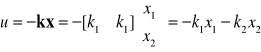
Stąd podstawiając sterowanie do równania stanu otrzymujemy równanie stanu dla układu zamkniętego:

Równanie charakterystyczne układu zamkniętego ma postać:

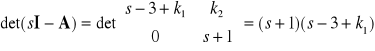
System zamknięty jest stabilny, jeżeli
.

Projektowanie układu sterowania ze sprzężeniem od stanu składa się z następujących kroków:

1. Na podstawie znajomości wymaganych wartości pierwiastków równania charakterystycznego układu zamkniętego wyznaczamy zadane równanie charakterystyczne.

2. Przyjmujemy
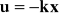
   i wyznaczamy równanie charakterystyczne układu zamkniętego.

3. Porównując zadane równanie charakterystyczne i równanie układu zamkniętego zapisujemy układ równań liniowych.

4. Rozwiązując układ równań obliczamy wzmocnienia
   .

Transmitancja równoważnego kompensatora

Transmitancja równoważnego kompensatora umożliwia porównanie otrzymanych wyników projektowania z wynikami otrzymanymi podczas projektowania metodami klasycznymi.

Równania systemu o jednym wejściu i jednym wyjściu:

, (2.4)

. (2.5)

Transformaty Laplace'a równania stanu ma postać:

(2.6)

Stąd

(2.7)

gdzie

. (2.8)

Transformata Laplace'a równania wyjścia

. (2.9)

Stąd transmitancja operatorowa systemu ma postać:

. (2.10)

Transformatę sygnału sterującego u określa wyrażenie

(2.11)

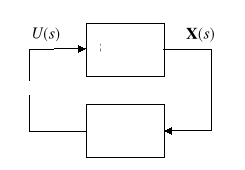
Rys. 7. Regulacja w układzie ze sprzężeniem od stanu

Transmitancja układu otwartego ma postać

(2.12)

Dla równoważnego układu projektowanego metodą klasyczną

, (2.13)

gdzie

− transmitancja kompensatora (regulatora),

− transmitancja systemu (obiektu).

Porównując (2.12) i (2.13) otrzymujemy

. (2.14)

Obliczając K(s) można wyznaczyć charakterystyki częstotliwościowe, zapas stabilności, pasmo przenoszenia, wykres linii pierwiastkowych.

3. Projektowanie obserwatora stanu

Wady układu regulacji ze sprzężeniem od stanu:

- wymagana znajomość wszystkich zmiennych stanu,

- wymagane są idealne czujniki pomiarowe o nieograniczonym paśmie,

- stosowanie wielu czujników pomiarowych może być technologicznie niemożliwe lub kosztowne,

- uszkodzenie nawet jednego czujnika może spowodować niestabilność układu regulacji.

W praktyce stosuje się kompensatory, które wykorzystują jedynie sygnały wejściowe i wyjściowe obiektu regulacji − układy ze sprzężeniem wyjściowym.

Idea obserwatora stanu polega na wykorzystaniu sygnałów wejściowych i wyjściowych systemu do estymacji zmiennych stanu (D. Luenberger).

Jeżeli znane są wszystkie parametry systemu (macierze A, B, C, D), to można go zasymulować analogowo lub cyfrowo. Można w ten sposób odtworzyć wszystkie stany symulowanego systemu.

Załóżmy, że znany jest opis systemu

(3.1)

a stan początkowy

(3.2)

jest nieznany.

Symulowany system (obserwator stanu) można przedstawić w postaci

(3.3)

(3.4)

gdzie
oznacza znany stan początkowy symulowanego systemu. Błąd odtworzenia stanu definiuje zależność

. (3.5)

Stąd uwzględniając (3.1) i (3.3) otrzymuje się następujące równanie błędu odtworzenia stanu

(3.6)

z warunkiem początkowym

(3.7)

Rozwiązanie równania (3.6) ma postać

(3.8)

Błąd
dąży do zera, jeżeli system jest stabilny (
, gdy
). Błąd jest równy zero, jeżeli warunek początkowy systemu jest taki sam jak warunek początkowy obserwatora. Warunek początkowy systemu jest jednak nieznany. W obserwatorze określonym zależnościami (3.3) i (3.4) nie jest wykorzystywana informacja dostarczana przez sygnał wyjściowy systemu.

Załóżmy, że równanie wyjścia ma postać

. (3.9)

Wprowadzając do równania obserwatora człon korekcyjny, który porównuje sygnał wyjściowy systemu i obserwatora otrzymuje się

(3.10)

(3.11)

Równanie stanu dla błędu przyjmuje wtedy postać

(3.12)

(3.13)

Jeżeli wybierzemy L w taki sposób, aby wartości własne macierzy A − LC były arbitralnie ulokowane na płaszczyźnie zespolonej, to problem będzie rozwiązany. Błąd obserwatora będzie dążył do zera przy dowolnych warunkach początkowych.

Ta właściwość układu jest nazywana obserwowalnością.

Obserwowalność oznacza, że dobierając odpowiednio macierz L można ulokować wartości własne macierzy A − LC w dowolnym miejscu na płaszczyźnie zespolonej.

Liniowy układ stacjonarny

, (3.14)

. (3.15)

jest całkowicie obserwowalny wtedy i tylko wtedy, gdy rząd macierzy obserwowalności

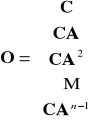
(3.16)

ma rząd równy n.

Funkcja Control System Toolbox
oblicza wartości macierzy L dla zadanych biegunów obserwatora OP macierzy A − LC.

• Bieguny obserwatora powinny być tak dobierane, aby zapewnić szybką zbieżność błędu estymacji
  

• Bieguny obserwatora powinny być większe (kilkakrotnie) od biegunów układu regulacji (macierzy A − Bk).

Równanie charakterystyczne obserwatora można zapisać w postaci

lub

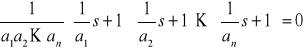
Decydujący wpływ na szybkość działania obserwatora ma największa stała czasowa
.

Bieguny obserwatora nie mogą się znajdować zbyt daleko w lewej półpłaszczyźnie ponieważ:

• wartości k i L będą duże i mogą spowodować wystąpienie nasycenia sygnałów a nawet niestabilność układu,

• nastąpi zwiększenie pasma przenoszenia, co utrudni tłumienie zakłóceń o wysokiej częstotliwości.

Zasada separacji estymacji stanu i sterowania

Projektowanie układu regulacji ze sprzężeniem od stanu i projektowanie obserwatora stanu są separowalne.

Oznacza to, że można zaprojektować układ regulacji przyjmując, że stan układu jest obserwowalny, a następnie zaprojektować obserwator stanu estymujący stan układu i wykorzystać oceny stanu zamiast stanu.

Równania stanu i obserwatora

Łącząc równania stanu obiektu i obserwatora otrzymuje się

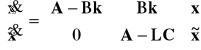
(3.17)

Ponieważ

,
,

Stąd

Analiza transmitancji

Równanie kompensatora szeregowego otrzymuje się jako połączenie równań opisujących sprzężenie od stanu i równań obserwatora

. (3.18)

Transformując (3.18) otrzymuje się równanie operatorowe

(3.19)

Transmitancja operatorowa korektora

. (3.20)

• Pomimo tego, że zarówno macierz regulatora
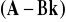
  jak macierz kompensatora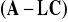
  będą stabilne, to macierz kompensatora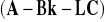
  może być niestabilna (może mieć bieguny w prawej półpłaszczyźnie zmiennej zespolonej).

• Regulatory zbudowane z zastosowaniem obserwatorów nie mają cechy odporności - wykazują dużą czułość na zakłócenia i zmiany parametrów)

• Regulatory zbudowane z zastosowaniem obserwatorów mają mniejszy zapas stabilności w porównaniu z regulatorami ze sprzężeniem od stanu

Układ zamknięty otrzymuje się łącząc szeregowo obiekt i kompensator.

Wielkość zadaną można uwzględnić przyjmując

N - wzmocnienie statyczne wejścia wielkości zadanej dobrane tak, aby błąd statyczny dla wymuszenia skokowego był równy zero.

Rys. 8. Regulacja w układzie ze sprzężeniem od stanu obserwowanego

1. obserwator RZĘDU ZREDUKOWANEGO

Obserwator rzędu pełnego ma rząd taki sam jak rząd systemu. Jeżeli rząd systemu jest równy n, a m zmiennych stanu jest dostępnych pomiarowo (mierzalnych), to odtwarzanie wszystkich zmiennych stanu nie jest konieczne. Można wtedy odtwarzać jedynie
nieznanych zmiennych stanu systemu. Obserwator taki został po raz pierwszy zaproponowany przez D. Luenbergera.

Aby wyprowadzić równanie obserwatora rzędu zredukowanego, definiuje się liniową transformację stanu

(4.1)

(4.2)

gdzie: z jest wektorem o wymiarze

T jest dowolną macierzą o wymiarach
która spełnia warunek, że macierz

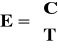
jest nieosobliwa.

Macierz
istnieje, jeżeli
. Łącząc wektory y i z otrzymujemy

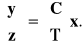
(4.3)

Stąd

.

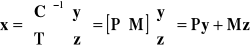
Załóżmy, że konstruujemy obserwator rzędu pełnego

(4.4)

gdzie
jest oceną z. Z (4.4) wynika, że aby estymować x, należy jedynie zaprojektować estymator z. W tym celu należy jedynie wyznaczyć równanie różniczkowe opisujące stan zredukowany z. Mnożąc lewostronnie równanie stanu przez E otrzymujemy

.

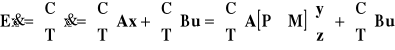
Z (4.3) otrzymujemy

.

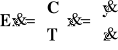
Stąd

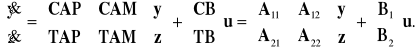
(4.5)

Z (4.5) wynika, że

(4.6)

Obserwator rzędu pełnego dla z

(4.7)

- sygnał wejściowy obserwatora,

- człon korekcyjny, którego zadaniem jest stabilizowanie błędu obserwatora.

Ponieważ
jest macierzą odwrotną E, to
i
.

.

Człon korekcyjny nie zapewnia więc żadnej korekcji, ponieważ zawsze jest równy 0. Dlatego w członie korekcyjnym wykorzystywana jest pochodna y zamiast y.

Z równania (4.5) mamy

(4.8)

Równanie obserwatora

(4.9)

Aby wykazać poprawność pracy obserwatora, należy udowodnić, że błędy estymacji są asymptotycznie zbieżne do zera. Inaczej można powiedzieć że, układ równań różniczkowych opisujących błąd powinien być asymptotycznie stabilny. Odejmując
od z, (4.9) od (4.6), otrzymujemy

. (4.10)

W równaniu błędu (4.10) występuje nieznana macierz L. Problem polega na tym, czy można dobrać L w taki sposób, aby rozmieścić wartości własne (bieguny) macierzy
w dowolny sposób lub przynajmniej tak, aby zapewnić stabilność układu (4.10).

Luenberger wykazał, że obserwowalność pary (C,A) jest równoważna obserwowalności pary
Dlatego można dobrać taką macierz L, aby przemieścić wartości własne macierzy
w dowolne miejsce na płaszczyźnie zespolonej.

Wprowadźmy zmienną w

(4.11)

Obserwator rzędu zredukowanego można zapisać w następującej postaci:

(4.12)

(4.13)

gdzie:

,

W przypadku szczególnym, jeżeli
, można wybrać
. Otrzymuje się wtedy
i żadna transformacja nie jest potrzebna. Macierze A i B mogą być wtedy podzielone w bezpośredni sposób, aby otrzymać

5. DYSKRETNY FILTR KALMANA

5.1. Sformułowanie problemu

Niestacjonarny dyskretny system dynamiczny:

, (5.1)

. (5.2)

Cel: wyznaczyć ocenę stanu
.

Założenia:

• macierze
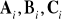
  znane,

• 
  − szum systemowy (błędy modelowania, niedoskonałość elementów wykonawczych, zakłócenia wewnętrzne),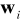

• 
  − szum pomiarowy (niedoskonałość czujników pomiarowych),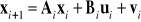

• 
  

• 
  ,

• 
  ,

• 
  ,
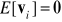
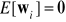
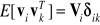
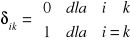
  − delta Kroneckera,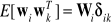

• 
  ,

• 
  

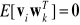
Zakłócenia
mają właściwości dyskretnego białego szumu (nieskorelowane, o zerowej wartości oczekiwanej).

• 
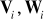
  − znane dodatnio określone macierze

• stan początkowy
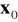
  jest nieznany,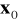
  jest zmienną losową o znanej wartości oczekiwanej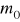
  i macierzy kowariancji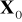
  .

Niektóre z tych założeń można zastąpić przez mniej restrykcyjne, np.

• niezerowe wartości oczekiwane szumów
  ,

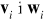
• skorelowane
  ,

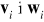
• osobliwa macierz
  ,

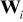
• wzajemnie skorelowane
  .

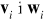
1. Identyfikacja parametrów systemu o wielu wyjściach metodą rekurencyjną najmniejszych kwadratów

Równanie regresji (model) systemu o n_y wyjściach ma postać

, (5.3)

− (n_p×1) − wektor parametrów,

R_i − (n_p× n_y) − macierz regresji,

Minimalizowany wskaźnik − ważona suma regresji

, (5.4)

Q_i − (n_y× n_y) macierz symetryczna, dodatnio określona.]

Wektor
można obliczyć w podobny sposób jak dla systemu o jednym wyjściu

(5.5)

(5.6)

(5.7)

Nawet, jeżeli macierz
jest znana z góry (a priori), w każdej iteracji należy obliczać macierz odwrotną
. Macierz P_i może być interpretowana jako macierz kowariancji błędu estymacji
pod warunkiem, że Q_i jest macierzą odwrotną kowariancji szumu pomiarowego.

2. System statyczny bez szumu systemowego

, (5.8)

. (5.9)

Załóżmy że:

• 
  ,

• 
  ,

• 
  

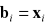
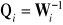
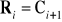
Stosując przy powyższych oznaczeniach algorytm rekurencyjny najmniejszych kwadratów otrzymujemy

, (5.10)

, (5.11)

, (5.12)

. (5.13)

P_i jest macierzą kowariancji błędu estymacji stanu
.

1. System dynamiczny z szumem systemowym

, (5.14)

. (5.15)

Stan systemu zmienia się (ewoluuje) w czasie ze względu na dynamikę systemu. Szum systemowy powoduje jednak, że pomimo znajomości macierzy
nie można dokładnie obliczyć przyszłych wartości wektora stanu. Wprowadzimy dlatego następujące rozróżnienie ocen wektora stanu:

• predykcja
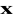
  i P w chwili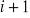
  na podstawie informacji dostępnej w chwili i (wartości a priori)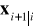
  ,
  ,

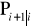
• aktualizacja
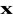
  i P w chwili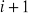
  po uwzględnieniu pomiarów zebranych w chwili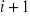
  (wartości a posteriori)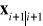
  ,
  .

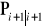
Predykcja
i P

Szum systemowy v_i jest ciągiem niezależnych wektorów losowych o zerowej wartości oczekiwanej. Dlatego obliczając predykcję
można zastąpić v_i jego wartością oczekiwaną

. (5.16)

Jeżeli predykcja jest nieobciążona,
, co jest spełnione, jeżeli
, to macierz błędu predykcji

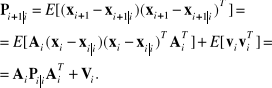
(5.17)

Błąd predykcji

. (5.18)

Aktualizacja
i P

Oceny wartości
i
można ulepszyć uwzględniając wyniki pomiarów w chwili
. W tym celu zastępujemy
przez
, a
przez
. Odpowiada to wykonaniu jednego kroku dla problemu statycznego, ponieważ prawdziwa wartość
nie zmienia się podczas aktualizacji oceny.

Równania dla systemu statycznego mogą być wtedy wykorzystane pod warunkiem dokonania zmian oznaczeń dla odróżnienia wartości a priori i a posteriori
i

• 
  →
  ,

• 
  →
  ,

• 
  →
  ,

• 
  →
  .

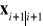
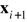
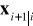
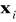
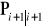
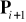
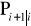
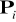
Załóżmy, że
i
są znane.

Następujący algorytm umożliwia obliczanie ocen
i
:

• Predykcja stanu i macierzy kowariancji błędu predykcji

, (5.19)

(5.20)

• Obliczenie wzmocnienia (macierzy) filtru

. (5.21)

• Aktualizacja oceny stanu

. (5.22)

• Aktualizacja oceny macierzy kowariancji

. (5.23)

Można sprawdzić, że podobnie jak w metodzie najmniejszych kwadratów
. Powyższe równania umożliwiające obliczanie
na podstawie
są nazywane filtrem estymującym.

Uwagi.

1. Aby obliczyć
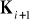
   należy obliczyć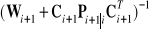
   , co jest zawsze możliwe, jeżeli macierz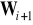
   jest nieosobliwa. W przypadku braku szumu pomiarowego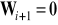
   , pojawiają się trudności wymagające specjalnych rozwiązań.

2. Filtr estymujący można transformować w filtr predykcyjny, który oblicza
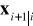
   z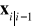
   .

Ponieważ

,

,

to filtr predykcyjny określa wyrażenie

, (5.24)

(5.25)

3. Istotną zaletą filtru Kalmana jest jego rekurencyjna postać, która umożliwia obliczenia metodą on-line. Aby zmniejszyć nakład pracy obliczeniowej on-line, można obliczać metodą off-line wszystkie wielkości, które nie są zależne od pomiarów.

Inicjalizacja filtru

Jeżeli wartość oczekiwana
i macierz kowariancji
stanu początkowego
są znane, to można przyjąć

,

.

Można również przez analogię z metodą najmniejszych kwadratów przyjmować

,

,

jeżeli nie mamy zaufania do oceny stanu początkowego.

5. Filtr stacjonarny

Załóżmy, że system jest stacjonarny (macierze A, B i C stałe) oraz, że szumy
mają stacjonarne statystyki (V i W stałe).

Jeżeli para (C, A) jest detektowalna (nieobserwowalne bieguny A są stabilne), to
dąży do stałej macierzy P, gdy

,

.

Z zależności na
otrzymujemy

(5.26)

Uwzględniając wyrażenia określające
i
można napisać

. (5.27)

Mnożąc (5.27) lewostronnie przez
i prawostronnie przez
i zastępując
przez
otrzymuje się równanie Riccati'ego

. (5.28)

Macierz
może być obliczana:

• poprzez rozwiązanie równania macierzowego (5.28),

• symulując zależność (5.20) określającą
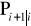
  , aż macierz kowariancji ustali się.

Wzmocnienie stacjonarnego filtru Kalmana

. (5.29)

Realizacja filtru stacjonarnego jest szczególnie prosta, ponieważ predykcję stanu i aktualizację jego estymaty można połączyć w jedno równanie

. (5.30)

Stąd otrzymuje się

. (5.31)

Projektowanie układów sterownia optymalnego przy kwadratowym wskaźniku jakości

Rozwój metod sterowania przy kwadratowym wskaźniku jakości (LQR) rozpoczął się w latach sześćdziesiątych. Zakłada się, że obiekt jest liniowy i znany jest jego opis w przestrzeni stanów. Zadanie polega na wyznaczeniu sterowania minimalizującego kwadratowy wskaźnik jakości.

Zakłada się ponadto, że system znajduje się w stanie równowagi. Celem sterowania jest utrzymanie systemu w stanie równowagi lub w zadanym punkcie pracy pomimo oddziałujących zakłóceń. Zadania regulacji typu nadążnego mogą być przekształcone do problemu regulacji stałowartościowej.

Założenie stanu ustalonego umożliwia rozszerzenie horyzontu optymalizacji do nieskończoności. Przyjęcie horyzontu skończonego prowadzi do rozwiązań regulatorów typu niestacjonarnego, które są trudniejsze do analizy i implementacji.

5.1. Problem sterowania optymalnego przy kwadratowym wskaźniku jakości

Równania systemu

, (6.1)

. (6.2)

Kwadratowym wskaźnik jakości

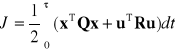
. (6.3)

Q - macierz symetryczna dodatnio półokreślona,

R - macierz symetryczna dodatnio określona,

• - horyzont optymalizacji.

Zadanie polega na wyznaczeniu
minimalizującego wskaźnik jakości (6.3).

Dla systemu rzędu pierwszego wskaźnik jakości przyjmuje postać

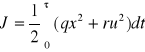
. (6.4)

Wskaźnik reprezentuje ważoną sumę energii sterowania i stanu (dokładności sterowania). Jeżeli r jest bardzo duże, energia sterowania musi być niewielka, aby zapewnić niewielką wartość wskaźnika. Można wtedy stosować mniejsze silniki, elementy wykonawcze, wzmacniacze, itp. Jeżeli q jest większe od r, otrzymuje się układ zamknięty o dużym tłumieniu (bez wielkich zmian i przeregulowań).

6.2. Rozwiązanie zadania starowania optymalnego przy wykorzystaniu zasady minimum Pontriagina

Zadania sterowania optymalnego mogą być rozwiązywane przy wykorzystywaniu różnych metod, między innymi:

• równań Eulera-Lagrange'a,

• teorii Hamiltona-Jacobi-Bellmana,

• zasady minimum Pontriagina.

Hamiltonian

(6.5)

Zasada minimum mówi, że sterowanie optymalne i trajektoria stanu muszą spełniać następujące równania:

1. Równania stanu

(6.6)

2. Równania stanu sprzężonego

, (6.7)

3. Warunek minimum

(6.8)

Uwzględniając zasady różniczkowania zależności (6.1)− (6.3) otrzymuje się

, (6.9)

(6.10)

, (6.11)

- sterowanie optymalne

Równania (6.9) i (6.10) są sprzężonymi liniowymi równaniami różniczkowymi. Tworzą one dwupunktowy problem graniczny ze względu na różne warunki graniczne początkowe i końcowe. Problem ten jest trudny do rozwiązania numerycznego.

Podstawiając sterowanie optymalne do równań stanu (6.1) i stanu sprzężonego (6.7)

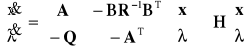
, (6.12)

H − macierz Hamiltonianu.

Aby wyznaczyć sterowanie optymalne w ogóle nie trzeba rozwiązywać dwupunktowego problemu granicznego. Można to wykazać podstawiając

. (6.13)

Różniczkując obie strony (6.13) względem czasu i uwzględniając (6.12)

. (6.14)

Z (6.12) mamy także

. (6.15)

Stąd na podstawie (6.14) i (6.15) można napisać

. (6.16)

Równanie Riccatiego (6.16) − nieliniowe macierzowe równanie różniczkowe, musi być rozwiązywane wstecznie w czasie ze względu na warunki końcowe. Rozwiązując równanie Riccatiego unika się rozwiązywania dwupunktowego problemu granicznego.

Powyższe sformułowanie problemu LQR jest znane jako problem o horyzoncie skończonym. Jako wynik otrzymuje się regulator niestacjonarny

, (6.17)

. (6.18)

W problemie o horyzoncie nieskończonym
. Wskaźnik jakości musi być zbieżny, aby istniał regulator optymalny.

Jeżeli istnieje sterowanie optymalne, to układ zamknięty może być niestabilny.

Macierz P(t) dąży do stałej macierzy P, jeżeli spełnione są następujące warunki:

1. System jest stabilizowalny. Niestabilne bieguny macierzy A są sterowalne.

Warunek sterowalności:

,

2. Macierz R jest dodatnio-określona

3. Macierz Q może być sfaktoryzowana w następujący sposób:
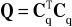
   , przy czym para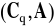
   jest detektowalna.

System jest detektowalny, jeżeli jego niestabilne bieguny są obserwowalne lub, równoważnie, nieobserwowalne bieguny są stabilne.

Ponieważ
, równanie Riccatiego staje się wtedy nieliniowym macierzowym równaniem algebraicznym

(6.19)

i układ zamknięty jest asymptotycznie stabilny.

6.3. Uogólnienie problemu LQR

Uwzględnienie mieszanych iloczynów we wskaźniku jakości

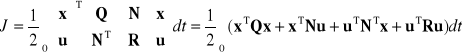
. (6.20)

Równanie Riccatiego

. (6.21)

Sterowanie optymalne

, (6.22)

. (6.23)

6.4. Regulatory o zadanym stopniu stabilności

Regulator można zaprojektować tak, aby bieguny były umieszczone α jednostek na lewo od osi urojonej (im dalej na lewo tym szybsze działanie układu). Można to osiągnąć przyjmując jako wskaźnik jakości

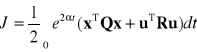
. (6.24)

Równanie Riccatiego

. (6.25)

Sterowanie optymalne

, (6.26)

. (6.27)

6.5. Funkcje MATLABa

[K,P,ev] = lqr(A,B,Q,R,N)

[K,P,ev] = lqry(A,B,C,D,Q,R)

ev − wartości własne macierzy układu zamkniętego.

Funkcja lqry służy do rozwiązywania szczególnego przypadku, gdy funkcja kosztu jest równa

.

X = are(A,B,C) − służy do rozwiązywania algebraicznego równania Riccatiego.

7. REGULACJA CyFROWA

Rys. 9. Schemat układu regulacji cyfrowej

Równanie różnicowe

,

.

Równanie różniczkowe

. (7.1)

Najprostsza metoda aproksymacji pochodnej

(7.2)

gdzie
, T oznacza okres próbkowania. Podstawiając (7.2) do (7.1) otrzymujemy

Widmo sygnału spróbkowanego

Rys. 10. Sygnał ciągły i próbkowany

Sygnał dyskretny można modelować jako iloczyn ciągu przesuniętych impulsów Dirac'a i sygnału ciągłego

. (7.3)

Ciąg impulsów Dirac'a można przedstawić w postaci szeregu Fouriera

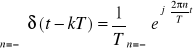
. (7.4)

Transformatę Fouriera sygnału dyskretnego można wyrazić za pomocą wzoru

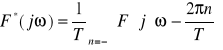
. (7.5)

7

---