WFiIS |
Imię i nazwisko: 1. Zyśko Tomasz 2. Zychowicz Mateusz |
ROK 2 |
GRUPA 1 |
ZESPÓŁ 9 |
|||
PRACOWNIA FIZYCZNA I i II |
TEMAT: Mostek Wheatstone'a |
NR ĆWICZENIA 32 |
|||||
Data wykonania: 2. 10. 2005 |
Data oddania: |
Zwrot do poprawy: |
Data oddania: |
Data zaliczenia: |
OCENA |
||
Cel ćwiczenia :
Pomiar nieznanych oporów oraz ich połączeń szeregowych, równoległych i mieszanych.
Wprowadzenie :
Znalezienie wielkości napięć i prądów płynących w poszczególnych częściach obwodu elektrycznego jest zagadnieniem podstawowym w konstrukcji układów o różnym przeznaczeniu. Rozwiązywanie obwodów prądu stałego opiera się na następujących prawach :
Stosunek napięcia między końcami przewodnika do natężenia prądu jest wielkością stałą, nazywaną opornością ( prawo Ohma )
W węzłach sieci, tzn. w punktach wspólnych dla trzech lub więcej przewodów algebraiczna suma natężeń wpływających i wypływających z węzła musi być równa zeru
( I prawo Kirchhoffa ).
Suma różnic potencjałów obliczonych kolejno wzdłuż zamkniętej pętli sieci - tzn. drogi, która rozpoczyna się i kończy w tym samym węźle, równa się zeru ( II prawo Kirchhoffa ).
Warunki powyższe zapisuje się w postaci algebraicznego układu takiej liczby niezależnych równań liniowych, która pozwala na jednoznaczne znalezienie poszukiwanych prądów.
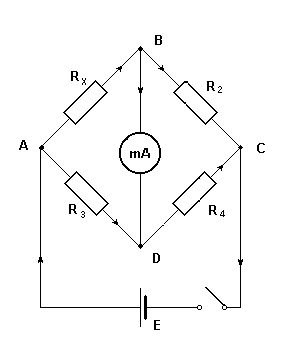
Mostek Wheatstone`a jest układem do pomiaru (porównywania) oporów. Tworzy go połączenie czterech oporów : Rx, R2, R3, R4 oraz galwanometru o oporze R5. Mostek jest zasilany z ogniwa galwanicznego lub zasilacza.
Jeśli dana jest siła elektromotoryczna oraz opory Rx, R2, R3, R4, R5, można znaleźć natężenia wszystkich prądów płynących w mostku.
Metoda mostka Wheatstone`a polega na porównywaniu oporów na tzw. równoważeniu mostka, tzn. na takim dopasowaniu oporów, aby prąd I5 płynący przez galwanometr był równy zero, wówczas możemy eksperymentalnie wyznaczyć Rx korzystając z wyrażenia:
.
Mostek Wheatstone'a używany w ćwiczeniu:
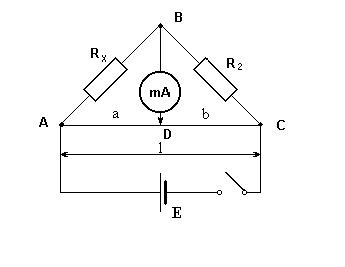
Prąd płynący z ogniwa galwanicznego E rozgałęzia się w punkcie A. Jedna jego część płynie przez szeregowo połączone opory Rx i R2, druga przez przewód AC. Przez zmiany położenia punktu D zmienia się stosunek oporów R3 do R4. Na odcinku BD prąd nie będzie płynął, jeżeli
Ponieważ RAD i RDC są oporami odcinków tego samego jednorodnego drutu, ich wielkości są proporcjonalne do długości:
Ponadto b jest różnicą całkowitej długości drutu l i odległości a, b=l-a. Ostatecznie otrzymujemy:
Co pozwala na łatwe wyznaczenie nieznanego oporu z pomiaru położenia suwaka.
Wyniki pomiarów :
Pomiary wstępne
Długość drutu ![]()
100cm
Błąd pomiaru długości drutu ![]()
Estymator odchylenia standardowego: 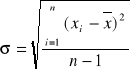
Estymator odchylenia standardowego średniej: U(x)=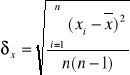
dla 10 pomiarów korzystamy ze wzoru: ![]()
= 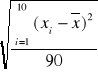
![]()
= ![]()
Pomiary dla rezystora RX1
Lp. |
a [cm] |
Opór wzorcowy R2
[ |
Opornik nieznany RX1
[ |
|
1 |
50,0 |
54 |
54,00 |
0,9655 |
2 |
43,5 |
70 |
53,89 |
0,7681 |
3 |
40,3 |
80 |
54,00 |
0,9721 |
4 |
37,3 |
90 |
53,54 |
0,2738 |
5 |
36,0 |
95 |
53,44 |
0,1765 |
6 |
34,3 |
100 |
52,21 |
0,6568 |
7 |
25,8 |
150 |
52,16 |
0,7414 |
8 |
20,8 |
200 |
52,53 |
0,2422 |
9 |
17,3 |
250 |
52,30 |
0,5183 |
10 |
14,8 |
300 |
52,11 |
0,8185 |
Wartość średnia |
|
|
|
|
![]()
= 0,82
U(![]()
)=0,26 [![]()
]
Opór RX1 jest równy 53,02[![]()
] z niepewnością 0,26 [![]()
]
Pomiary dla rezystora RX2
Pomiary Lp. |
a [cm] |
Opór wzorcowy R2
[ |
Opornik nieznany RX2
[ |
|
1 |
50,0 |
100 |
100,00 |
0,3913 |
2 |
45,2 |
120 |
98,98 |
0,1571 |
3 |
41,4 |
140 |
98,91 |
0,2177 |
4 |
38,2 |
160 |
98,90 |
0,2254 |
5 |
33,2 |
200 |
99,40 |
0,0007 |
6 |
29,3 |
240 |
99,46 |
0,0078 |
7 |
26,2 |
280 |
99,40 |
0,0009 |
8 |
23,7 |
320 |
99,40 |
0,0005 |
9 |
22,1 |
350 |
99,29 |
0,0065 |
10 |
20,0 |
400 |
100,00 |
0,3913 |
Wartość średnia |
|
|
|
|
![]()
= 0,39
U(![]()
)=0,12 [![]()
]
Opór RX2 jest równy 99,37[![]()
] z niepewnością 0,12[![]()
]
Pomiary dla rezystora RX3
Pomiary Lp. |
a [cm] |
Opór wzorcowy R2
[ |
Opornik nieznany RX3
[ |
|
1 |
50,1 |
36 |
36,14 |
0,0727 |
2 |
42,1 |
50 |
36,36 |
0,0034 |
3 |
37,8 |
60 |
36,46 |
0,0024 |
4 |
34,4 |
70 |
36,71 |
0,0861 |
5 |
31,4 |
80 |
36,62 |
0,0417 |
6 |
28,9 |
90 |
36,58 |
0,0284 |
7 |
26,8 |
100 |
36,61 |
0,0396 |
8 |
24,9 |
110 |
36,47 |
0,0033 |
9 |
19,5 |
150 |
36,34 |
0,0062 |
10 |
15,2 |
200 |
35,85 |
0,3190 |
Wartość średnia |
|
|
|
|
![]()
= 0,26
U(![]()
)=0,08 [![]()
]
Opór RX3 jest równy 36,41 [![]()
] z niepewnością 0,08 [![]()
]
Rezystory RX2 i RX3 połączone szeregowo:
Pomiary Lp. |
a [cm] |
Opór wzorcowy R2
[ |
Opornik nieznany RXsz
[ |
|
1 |
49,5 |
140 |
137,23 |
0,2862 |
2 |
43,5 |
180 |
138,58 |
0,6747 |
3 |
40,7 |
200 |
137,27 |
0,2446 |
4 |
35,4 |
250 |
137,00 |
0,5864 |
5 |
33,1 |
280 |
138,54 |
0,5967 |
6 |
28,7 |
340 |
136,86 |
0,8178 |
7 |
26,6 |
380 |
137,71 |
0,0027 |
8 |
24,8 |
420 |
138,51 |
0,5595 |
9 |
23,1 |
460 |
138,18 |
0,1737 |
10 |
21,6 |
500 |
137,76 |
0,0001 |
Wartość średnia |
|
|
|
|
Wartość teoretyczną ![]()
obliczam ze wzoru na połączenie szeregowe dwóch rezystorów:
![]()
= 99,37 + 36,41 = 135,78 [![]()
]
Porównując wartość średnią z wartością teoretyczną obliczam:
![]()
|137,76 - 135,78| = 1,98 [![]()
]
Błąd U(![]()
) obliczany jest z prawa przenoszenia błędów:
U(![]()
) =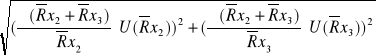
=![]()
=0.14[]
Opór RXsz jest równy 137,76 [![]()
] z niepewnością rozszerzoną 0,14 [![]()
]
Rezystory RX2 i RX3 połączone równolegle:
Pomiary Lp. |
a [cm] |
Opór wzorcowy R2
[ |
Opornik nieznany RXr
[ |
|
1 |
50,40 |
27 |
27,44 |
0,0903 |
2 |
44,00 |
35 |
27,50 |
0,0557 |
3 |
38,10 |
45 |
27,70 |
0,0015 |
4 |
33,5 |
55 |
27,71 |
0,0009 |
5 |
30,0 |
65 |
27,86 |
0,0147 |
6 |
25,8 |
80 |
27,82 |
0,0065 |
7 |
23,6 |
90 |
27,80 |
0,0042 |
8 |
21,7 |
100 |
27,71 |
0,0005 |
9 |
18,9 |
120 |
27,97 |
0,0527 |
10 |
16,6 |
140 |
27,87 |
0,0168 |
Wartość średnia |
|
|
|
|
Wartość teoretyczną ![]()
obliczam ze wzoru na połączenie równoległe dwóch rezystorów:
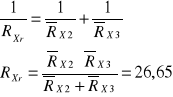
Porównując wartość średnią z wartością teoretyczną obliczam:
![]()
|27,74 - 26,65| = 1,09 [![]()
]
Błąd U(![]()
) obliczany jest z prawa przenoszenia błędów:
U(![]()
)=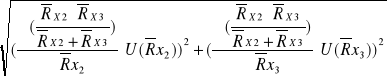
=
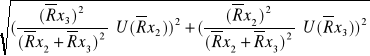
=0.04 []
Opór RXr jest równy 27,74 [![]()
] z niepewnością rozszerzoną 0,04 [![]()
]
Połączenie równoległe dwóch szeregowo połączonych rezystorów![]()
i![]()
z rezystorem ![]()
.
Pomiary Lp. |
a [cm] |
Opór wzorcowy R2
[ |
Opornik nieznany RXm
[ |
|
1 |
49,7 |
31 |
30,60 |
0,9154 |
2 |
42,5 |
40 |
29,57 |
0,0117 |
3 |
39,6 |
45 |
29,50 |
0,0289 |
4 |
37,1 |
50 |
29,49 |
0,0332 |
5 |
35,0 |
55 |
29,62 |
0,0034 |
6 |
33,0 |
60 |
29,55 |
0,0147 |
7 |
29,7 |
70 |
29,57 |
0,0100 |
8 |
27 |
80 |
29,59 |
0,0071 |
9 |
24,8 |
90 |
29,68 |
0,0001 |
10 |
22,8 |
100 |
29,53 |
0,0195 |
Wartość średnia |
|
|
|
|
Wartość teoretyczną obliczam ze wzoru na połączenie równoległe dwóch szeregowo połączonych rezystorów ![]()
i![]()
z trzecim rezystorem ![]()
.
![]()
![]()
=![]()
= 29,39 [![]()
]
Porównując wartość średnią z wartością teoretyczną obliczam:
![]()
|29,67 - 29,39| = 0,28 [![]()
]
Błąd U(![]()
) obliczany jest z prawa przenoszenia błędów:
U(![]()
)=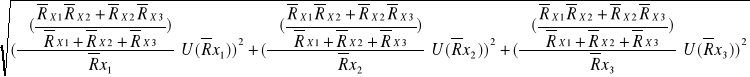
=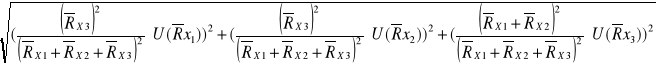
=0,27 [![]()
]
Opór RXm jest równy 29,39 [![]()
] z niepewnością rozszerzoną 0,27 [![]()
]
Rozrzut wartości oporu nieznanego dla RX3:
Przedział [ |
Liczba pomiarów |
|
< |
< 35,63 |
0 |
|
35,63 - 35,89 |
1 |
|
35,89- 36,15 |
1 |
|
36,15- 36,41 |
2 |
|
36,41- 36,67 |
5 |
|
36,67- 36,93 |
1 |
|
36,93 - 39,19 |
0 |
|
36,19> |
0 |
![]()
= 0,26
W przedziale od δ do δ powinno znaleźć się w przybliżeniu około wyników pomiarów. W naszym przypadku w przedziale tym znalazło się tam około 70% pomiarów. Natomiast w przedziale od δ do δ znalazło się 100% wyników pomiarów.
Testowanie hipotezy rozkładu normalnego
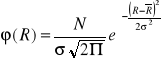
N - ilość wszystkich pomiarów
![]()
- odchylenie standardowe
Dla naszych wartości dla RX3:
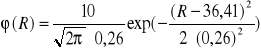
Rozkład krzywej Gaussa teoretyczny
Rozkład wyników uzyskanych w doświadczeniu pokrywa się z krzywą Gaussa (prawdopodobieństwem uzyskania ilości wyników w danym przedziale).
Wnioski
Doświadczenie pozwoliło nam wyznaczyć nieznane opory oraz potwierdziło wzory na opór zastępczy przy łączeniu szeregowym, równoległym i mieszanym oporów.
Różnice jakie występują pomiędzy wartościami obliczonymi a wartościami zmierzonymi dla tych połączeń nie mieszczą się w granicach błędu, który został policzony powyżej, jednak źródłem tych błędów było niedokładne przywieranie styku suwakowego do drutu, a co za tym idzie niestabilnej rezystancji co dla tak czułego układu pomiarowego jakim jest mostek miało duży wpływ.
6
Wyszukiwarka
Podobne podstrony:
laborka 32, WFiIS
32 piątek
32 sobota
od 24 do 32
32 pozyskujacy uczniow sluga bozy
32 Przepustka
ei 07 2002 s 32 34
PAG 32
09 1993 27 32
32 metoda pośreniego pomiaru długości
32 model małżeństwa i rodziny w XVII i XVII wieku, kulturoznawstwo
Unia Europejska t1.32, Wspólna polityla rolna
32. Małopłytkowość, MEDYCYNA VI rok, Pediatria, PEDIATRIA CAŁOŚĆ, Ustny PEDIATRIA Balwierz
Nr 32 BRĄZOWA
32 Dramat w okresie pozytywizmu i Młodej Polski (na tle dramatu europejskiego)
32 Geomorfologiczna charakterystyka wybranych obszarów Polski
32 oryginał
32 Swietlinska Outsourcing procesow
więcej podobnych podstron