1.

PRZEWODNICTWO ELEKTRYCZNE CIAŁ STAŁYCH

Przewodnictwo elektryczne w ciałach stałych. polega na ruchu nośników ładunków elektr., np. elektronów; wartość przewodnictwa zależy więc od liczby tych nośników w c. stałych Pod tym względem c. stałe. dzielą się na 3 grupy:
- przewodniki (metale),
- półprzewodniki
- dielektryki (izolatory).
Wraz ze wzrostem temp. przewodnictwo elektryczne przewodników (metali) maleje, natomiast w tempera turach bliskich 0°K staje się ono bardzo duże (nadprzewodnictwo). Przewodnictwo półprzewodników i dielektryków rośnie ze wzrostem temp.; w temp. niskich pół-przewodniki, praktycznie biorąc, nie przewodzą prądu elektr.
Możliwa jest również klasyfikacja ciał stałych ze względu na ich zdolność przewodzenia prądu elektrycznego pod wpływem przyłożonego z zewnątrz pola elektrycznego. Zdolność przewodzenia prądu elektrycznego określa się przez podanie przewodności właściwej lub jej odwrotności - oporu właściwego. Ciała stałe z tego punktu widzenia dzielimy na trzy grupy:
o dobre przewodniki (głównie metale) o δ od 10-8 do 10-6 Ω · m
o złe przewodniki (izolatory) o δ > 109 Ω · m
o ciała o pośrednich wartościach δ leżących w szerokich granicach około 14 rzędów wielkości. Do tej grupy ciał zaliczamy również półprzewodniki.
W półprzewodnikach mamy zawsze do czynienia z przewodnictwem elektronowym. Również przewodnictwo dziurowe polega, podobnie jak elektronowe, na przemieszczaniu się elektronów. Natomiast, np. w kryształach jonowych nośnikami prądu są jony, a nie elektrony. (Czasami przewodniki jonowe zaliczane są do półprzewodników, w szerszym sensie tego pojęcia).
Zależność oporu właściwego od temperatury T przebiega w sposób charakterystyczny, inny dla metali i inny dla półprzewodników:
o dla metali δ = δ0 (l +ΔT), gdzie T - temperatura, α - współczynnik temperaturowy oporu przyjmujący wartości dodatnie rzędu 10-6 na kelwin,
o dla półprzewodników δ = δ0eΔE/kT, gdzie k - stała Boltzmanna, ΔE - miara tzw. energii aktywacji. Jest to energia, jaką muszą mieć elektrony, aby mogły uczestniczyć w przewodzeniu prądu.

2.

Prawa Kirchhoffa- dwa podstawowe prawa dotyczące przepływu prądu stałego w obwodach:
I prawo Kirchhoffa: wektorowa suma wszystkich natężeń prądu dopływających do punktu rozgałęzienia w obwodzie elektrycznym równa jest zeru (inaczej: suma natężeń prądów wpływających do punktu rozgałęzienia równa jest sumie natężeń prądów wypływających).
II prawo Kirchhoffa: suma spadków napięcia w każdym zamkniętym obwodzie elektrycznym równa jest zewnętrznej sile elektromotorycznej SEM działającej na ten obwód.
Prawa Kirchhoffa pozwalają ułożyć i rozwiązać układ równań opisujący przepływ prądu stałego w dowolnie skomplikowanym obwodzie elektrycznym.

Prawo Ampčre'a - prawo określające siłę, z jaką pole magnetyczne o indukcji B działa na przewodnik, przez który płynie prąd o danym natężeniu I: dF = I (dL * B), gdzie dL - element przewodnika, dF - przyczynek siły działającej na element dL.

Prawo Ohma - prawo fizyki głoszące, że stały prąd I płynący w przewodniku jest wprost proporcjonalny do przyłożonego napięcia U (napięcie elektryczne). U=RI, gdzie współczynnik proporcjonalności R jest oporem elektrycznym (oporność elektryczna). Uogólnione prawo Ohma dla prądów zmiennych ma postać: ZI=e gdzie Z - zespolona oporność (impedancja), e - siła elektromotoryczna. Prawo odkrył G.S. Ohm.

3

Cykl Carnota - przemiana termodynamiczna, złożona z dwóch przemian izotermicznych i dwóch przemian adiabatycznych. Cykl Carnota jest procesem kołowym i odwracalnym. Do realizacji cyklu potrzebny jest czynnik termodynamiczny, który może wykonywać pracę np. gaz w naczyniu z tłokiem a także dwa nieograniczone źródła ciepła jedno jako źródło ciepła (o temperaturze T₁) a drugie jako chłodnica (o temperaturze T₂).

Przemiana izotermiczna - przemiana gazowa, zachodząca przy określonej, stałej temperaturze.

W przemianach tych, zgodnie z prawem Boyla'a-Mariotte'a, ciśnienie gazu doskonałego wywierane na ścianki naczynia jest odwrotnie proporcjonalne do zajmowanej przez niego objętości, co zapisuje się jako:

pV = const

gdzie:

p - ciśnienie

V - objętość

Przemiana adiabatyczna (Proces adiabatyczny) - proces termodynamiczny, podczas którego wyizolowany układ nie nawiązuje wymiany ciepła, lecz całość energii dostarczana lub odbierana jest z niego jako praca.

Przemiana adiabatyczna jest przemianą, w której zmieniają się trzy parametry stanu gazu: ciśnienie, objętość i temperatura. Przemiana ta nie wymaga ciepła z otoczenia, dlatego podczas sprężania rośnie jego temperatura, a podczas rozprężania temperatura maleje. Podobnie jak w przypadku sprężania izotermicznego - maleje objętość a rośnie ciśnienie, w sprężaniu adiabatycznym trzeba dodatkowo uwzględnić wzrost ciśnienia gazu (spowodowany wzrostem temperatury).

Przebieg przemiany adiabatycznej określa się prawem Poissona:

gdzie:

p - ciśnienie

V - objętość

- wykładnik adiabaty, równy stosunkowi pojemności cieplnej przy stałej objętości i przy stałym ciśnieniu.

Krzywe obrazujące procesy adiabatyczne zwiemy adiabatami. Proces adiabatyczny jest szczególnym przypadkiem procesu politropowego.

Przebieg cyklu

Cykl składa się z następujących procesów:

1. Sprężanie izotermiczne - czynnik roboczy styka się z chłodnicą, ma temperaturę chłodnicy i zostaje poddane procesowi sprężania w tej temperaturze (T₂). Czynnik roboczy oddaje ciepło do chłodnicy.

2. Sprężanie adiabatyczne - czynnik roboczy nie wymienia ciepła z otoczeniem, jest poddawany sprężaniu aż uzyska temperaturę źródła ciepła (T₁).

3. Rozprężanie izotermiczne - czynnik roboczy styka się ze źródłem ciepła, ma jego temperaturę i poddawany jest rozprężaniu izotermicznemu w temperaturze T₁, podczas tego cyklu ciepło jest pobierane ze źródła ciepła.

4. Rozprężanie adiabatyczne - czynnik roboczy nie wymienia ciepła z otoczeniem i jest rozprężany aż czynnik roboczy uzyska temperaturę chłodnicy (T₂).

Sprawność cyklu

Dla układu tego definiuje się sprawność jako stosunek pracy wykonanej do ilości ciepła pobranego ze źródła ciepła.

Parser nie umiał rozpoznać (Can't write to or create math output directory): \eta = \frac{Q _1 - Q _2}{Q_1} = \frac{T_1-T_2}{T_1} = 1- \frac{T_2}{T_1}

Wzór powyższy wyprowadzony przez Carnota określa, że sprawność cyklu nie zależy od czynnika roboczego, ani sposobu realizacji, a zależy tylko od temperatur źródła ciepła i chłodnicy.

Warto zwrócić uwagę na to, że sprawność silnika pracującego w temperaturach T₁=373K (temperatura wrzenia wody) i T₂=300K (temp. pokojowa) wynosi około 24%.

Carnot udowodnił też, że dowolny odwracalny cykl zamknięty w którym podczas pobierania ciepła układ ma temperaturę mniejszą od T_max a podczas oddawania ciepła większą od T_min ma sprawność mniejszą od cyklu Carnota opartego o temperatury T_max i T_min. Dlatego często sprawność silników termodynamicznych określa się w odniesieniu do cyklu Carnota zwanego silnikiem idealnym.

Cykl Carnota jest odwracalny i może przebiegać w odwrotnym kierunku (zamienione sprężanie z rozprężaniem) wówczas układ przekazuje energię cieplną od ciała o niższej temperaturze do ciała o wyższej temperaturze. Układ taki nazywany jest pompą ciepła (lub cieplną) i pracuje on kosztem wykonywania pracy nad nim. Sprawność cyklu Carnota określa też parametry idealnej pompy cieplnej działającej przy zadanych temperaturach. Rzeczywiste pompy cieplne mają sprawność mniejszą od cyklu Carnota.

[Edytuj]

Przykładowy diagram cyklu na wykresie ciśnienie vs. objętość

Źródło: "http://pl.wikipedia.org/wiki/Cykl_Carnota"

Cykl Carnota

Francuski inżynier i fizyk Leonarda Sadi Carnota na początku XIX-go wieku rozpatrywał tzw. cykl Carnota. Jest on cyklem odwracalnym składającym się z dwóch przemian izotermicznych oraz dwóch adiabatycznych. Przebieg tych przemian ilustruje

wykres:

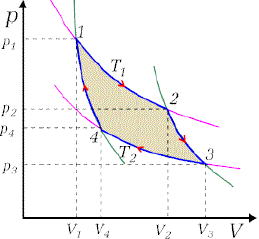
Na schemacie tym kolorem różowym zaznaczone są izotermy, kolorem zielonym - adiabaty. Ich odcinki, które wchodzą w skład cyklu, są oznaczone na niebiesko. Przebieg

cyklu rozpoczyna się w punkcie 1 przemianą izotermiczną zachodzącą przy temperaturze T1, w

wyniku której następuje rozprężanie gazu od objętości V1 do V2 przy czym ciśnienie zmienia się

od p1 do p2. Równocześnie ciepło pobierane jest ze zbiornika o nieograniczonej pojemności cieplnej, dzięki czemu jego temperatura nie ulega zmianie, pomimo przekazania układowi ciepła.

Proces zachodzący pomiędzy punktami 2 i 3 jest procesem adiabatycznym, natomiast proces w przedziale 3-4 jest znów procesem izotermicznym, ale zachodzącym przy niższej temperaturze T2; proces 4-1 jest drugim procesem adiabatycznym.

Przemiana	Parametry		Położenie cylindra	Ciepło pobrane	Ciepło oddane	Praca gazu	Praca sił zew.
Izotermiczna, rozprężanie	p1 V1 T1	p2 V2 T1	Z1	Q1		W1
Adiabatyczna, rozprężanie	p2 V2 T1	p3 V3 T2	p			W2
Izotermiczna, sprężanie	p3 V3 T2	p4 V4 T2	Z2		Q2		W3
Adiabatyczna, sprężanie	p4 V4 T2	p1 V1 T1	p				W4

Tabelka 1

Pierwsza przemiana zachodzi przy stałej temperaturze, wiec energia wewnętrzna gazu nie ulga

zmianie. Gaz pobiera ciepło Q1 ze źródła ciepła i w całości zużywa go na wykonanie pracy W₁.

W przemianie drugiej, zachodzącej pomiędzy punktami 2 i 3, gaz ulega rozprężeniu

adiabatycznemu. Oznacza to, że odcięty został zarówno dopływ ciepła, jak i możliwość przekazania

ciepła otoczeniu, ale rozprężanie odbywało się nadal do objętości V3.

Trzeci etap jest znów przemianą izotermiczną, w której gaz zostaje sprężony od objętości V3 do V4.

Gaz oddaje ciepło Q₂ do chłodnicy o wielkiej pojemności cieplnej, wiec temperatura T2 pozostaje

niezmieniona, ale wskutek rozprężania adiabatycznego od objętości V2 do V3, które zaszło

wcześniej, jest niższa od temperatury T1. Praca wykonana przez gaz w tym procesie wynosi W₂

W tym przypadku obie wielkości: wykonana praca i ciepło "pobrane" z chłodnicy są

ujemne. Ciepło oddane, któremu przypisujemy wartość dodatnią, oznacza się zwykle symbolem

Mamy więc

Czwarty proces jest znów adiabatyczny i przeprowadza układ od punktu 4 do początkowego punkt 1. W ten sposób cykl zostaje zamknięty. a energia wewnętrzna po wykonaniu całego cyklu ma swą

pierwotną wartość. Przyrost energii wewnętrznej układu równy jest zeru, a suma wykonanej

pracy, równa jest pobranemu przez układ ciepłu zgodnie ze wzorem:

Stosunek pracy wykonanej przez układ w jednym cyklu do pobranego w tym cyklu ciepła, nazywamy

sprawnością lub wydajnością silnika cieplnego (maszyny cieplnej). Silnik, którego cykl jest całkowicie odwracalny nazywamy silnikiem Carnota. Jest to silnik jedynie teoretyczny. Energię wewnętrzną (ciepło) zmienia na pracę mechaniczną.

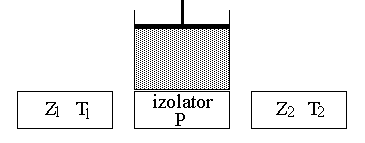
Silnik Carnota prezentuje schemat:

Składa się on z izolowanego cieplnie cylindra z tłokiem, oraz z trzech ruchomych płyt : Z₁, o temperaturze T₁, Z₂ o temperaturze T₂, oraz z izolatora P. Temperatura T₁>T₂ .

Praca wykonana przez siły zewnętrzne jest mniejsza od pracy wykonanej przez siły cieplne :

, ,

Sprawność silnika:

P_1,2,3 - ciśnienia wewnątrz cylindra; V_1,2,3 - objętości cylindra; T_1,2 - temperatura gazu wewnątrz cylindra; Q₁ - ciepło pobrane; Q₂ - ciepło oddane; W_1,2,3,4 - praca; W - praca wykonana przez silnik w czasie 1 cyklu; n - liczba moli; N_A - liczba Avogadra; N - ilość cząstek; k - stała Boltzmana; R - stała gazowa;  - sprawność.

Pierwsza zasada termodynamiki

 

Doświadczalną podstawą pierwszej zasady jest doświadczenie Joule'a i pokrewne mu, które dowodzą równoważności ciepła i pracy mechanicznej przez pokazanie możliwości całkowitej zamiany pracy na ciepło. Uznanie ciepła jako innego niż praca sposobu zmiany energii prowadzi w naturalny sposób do włączenie ciepła do zasady zachowania energii. Pierwsza zasada termodynamiki jest dokładnie tym prawem [Huang]:

 

Joule, Mayer (1842), Helmholtz (1847):
Zmiana energii wewnętrznej układu równa jest dostarczonemu do układu ciepłu i pracy wykonanej nad układem przez siły zewnętrzne:

U = Q + W

Konwencja: U to przyrost energii wewnętrznej układu. Q oznacza tu ciepło dostarczone do układu z zewnątrz. Jeśli jednak układ oddaje ciepło, wówczas jego energia wewnętrzna maleje; ciepło bierzemy ze znakiem ujemnym. W to praca wykonana nad układem przez siły zewnętrzne. Gdy zaś układ wykonuje pracę (jak to ma miejsce podczas rozprężania się gazu), jego energia maleje - pracę bierzemy ze znakiem ujemnym. Istnieją konwencje znaków różne od tutaj przyjętej.

 

I zasada termodynamiki pozwala na zdefiniowanie energii wewnętrznej jako funkcji stanu: dla wszystkich procesów prowadzących od pewnego określonego stanu do drugiego, zmiana U ma zawsze tą samą wartość, choć ilości dostarczanego ciepła i wykonanej pracy są na ogół różne dla różnych procesów.

  

Druga zasada termodynamiki

 Z doświadczenia wiemy, że są procesy zgodne z zasadą zachowania energii, które nigdy nie występują w przyrodzie. Na przykład, nigdy nie obserwujemy, by kamień leżący na podłodze spontanicznie się oziębił i wzniósł do sufitu, uzyskując kosztem ciepła energię potencjalną. Nie spodziewamy się też, by w słoneczny letni dzień zamarzł staw, oddawszy energię wewnętrzną otoczeniu. Zadaniem drugiej zasady termodynamiki jest włączyć do termodynamiki takie fakty doświadczalne, jej podstawą jest zdrowy rozsądek [Huang].

 Wszystkie poniższe sformułowania drugiej zasady termodynamiki są równoważne:

 

Clausius (1850): Nie istnieje proces termodynamiczny, którego jedynym wynikiem byłoby pobranie ciepła ze zbiornika chłodniejszego i przekazanie go do zbiornika cieplejszego (nie jest możliwe zbudowanie idealnej maszyny chłodzącej)

 

Kelvin (1851): Nie istnieje proces termodynamiczny, którego jedynym wynikiem byłoby pobranie ciepła ze zbiornika i całkowita zamiana tego ciepła na pracę mechaniczną.

 

Późniejsze od sformułowania Kelvina jest sformułowanie podane przy pomocy pojęcia silnika termodynamicznego

 

Planck: Nie możliwe jest zbudowanie silnika termodynamicznego pracującego cyklicznie, który całe pobrane ciepło zamieniałby na pracę (nie jest możliwe zbudowanie idealnego silnika cieplnego - czyli perpetuum mobile drugiego rodzaju).

 

Dla sprawności silnika cieplnego, z teorią których druga zasada jest związana, oznacza to, że sprawność silników cieplnych jest mniejsza od jedności

Druga zasada termodynamiki pozwala na zdefiniowanie bezwzględnej skali temperatur Kelvina identycznej ze skalą temperatury gazu doskonałego.

Pozwala ona też na wprowadzenie użytecznej funkcji stanu nazywanej entropią. Związana jest z pojęciem procesów odwracalnych i nieodwracalnych,z kierunkiem procesów zachodzących samorzutnie w układach izolowanych, z kierunkowością zjawisk w przyrodzie. Za pomocą pojęcia entropii druga zasada termodynamiki daje się wysłowić:

 Boltzmann: Entropia układu izolowanego nie maleje.

 Druga zasada termodynamiki nie jest ścisłym prawem przyrody, ma jedynie charakter statystyczny. Zdarzenia sprzeczne z nią mogą w rzeczywistości zajść, lecz są mało prawdopodobne. Ściślej mówiąc są tym mniej prawdopodobne, im więcej cząstek liczy układ termodynamiczny. II zasada termodynamiki dobrze sprawdza się w skali makro, gorzej w skali mikro. W zaawansowanym wykładzie mechaniki statystycznej dowodzi się nawet, że pewne wydarzenia sprzeczne z drugą zasadą termodynamiki z pewnością będą miały miejsce (twierdzenie Poincare'go o powrocie). Jednak czas, jaki przychodzi czekać na tego typu zajście w makroskopowym układzie, znacznie przekracza wiek wszechświata, możemy się więc „nie doczekać”...

7

Rys 1

---