Opracowanie wyników

Poniższe dwie tabele przedstawiają wartości kąta odchylenia dla widma 1 i 2 (ze strony lewej i prawej),dla fali niebieskiej, zielonej i dwóch żółtych. W tabelach zawarta też jest wartość współczynnika załamania dla wymienionych fal, wyliczona ze wzoru:

gdzie: d=175 nm, n - rząd widma

(d -szerokość szczeliny dyfrakcji)

WIDMO 1

	Niebieska.		Zielona		żółta 1		żółta 2
	P	L	P	L	P	L	P	L
	15,18	15,3	19,18	19,33	20,25	20,42	20,3	20,46
	15,16	15,24	19,14	19,34	20,23	20,42	20,27	20,49
	15,16	15,3	19,16	19,33	20,23	20,45	20,28	20,48
	15,17	15,25	19,15	19,32	20,22	20,43	20,27	20,48
war.śre.	15,21		17,22		20,335		20,38
	0,000459		0,000518		0,000607		0,000609
nm]	495		518		607		609

WIDMO 2

	31,48	32,11	41,2	42,5	44,15	44,49	44,28	45,01
	31,47	32,2	41,17	42,02	44,11	45,01	44,25	45,15
	31,48	32,18	41,19	42,05	44,13	44,5	44,26	45,1
	31,46	32,16	41,17	42,04	44,14	44,51	44,25	45,13
war.śre.	31,795		41,61		44,32		44,645
	0,00046		0,000581		0,000611		0,000614
[nm]	460		581		611		614

Błąd wyliczamy w tym przypadku w ten sposób, że jako błąd przyjmujemy średnią różnice wartości  uzyskanych z widma 1 i 2.

	1,75	63	3,5	5,25
[nm]

Wartość średnia =18.25 nm.

Poniższa tabela przedstawia wartości kąta minimalnego, wartość średnią oraz błąd.

Wartość średniej i błędy zarówno dla kąta minimalnego jak i dla kąta łamiącego policzone są odpowiednio z mediany i rozstępu.

	niebieski	Zielona	żółty
	54,25	52,11	51,2
	54,3	52,19	51,15
	54,29	52,18	51,13
	54,3	52,15	51,14
	54,28	52,14	51,13
war.śre	54,29	52,15	51,14
błąd śre.	0,01975	0,01975	0,02765
błąd poj.	0,008065	0,008065	0,01129

Tabela poniższa przedstawia wartości kąta łamiącego oraz wartość średnią i błąd.

wiąz.1	Wiąz.2	różnica	kąt łamiąc
54,10	66,28	120,38	60,19
54,11	66,27	120,38	60,19
54,09	66,20	120,29	60,15
54,10	66,31	120,41	60,21
54,13	66,30	120,43	60,22
		war.śre	60,19
		błąd.śre	0,0301
		błąd.poje.	0,013462

Wartość współczynnika załamania liczymy ze wzoru:

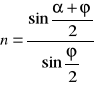
gdzie: α - kąt minimalny, ϕ - kąt łamiący

otrzymujemy:

	niebieska	Zielona	Żółta
współcz.n	1,67	1,65	1,64
błąd n	0,0835	0,0825	0,114

Błąd n liczymy korzystając z prawa przenoszenia błędów, biorąc wartości średnie kąta minimalnego i łamiącego oraz odpowiednie błędy średnich. Nie podajemy tu wzoru ponieważ obliczenia były dość skomplikowane i do jego obliczenia skorzystaliśmy z programu „Mathematica”.

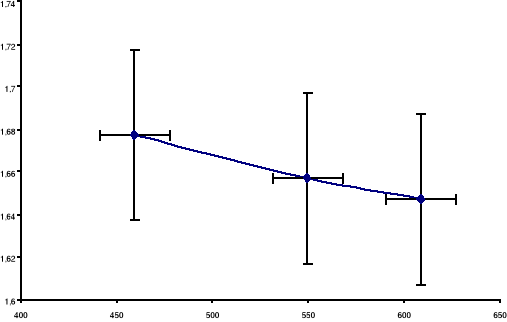
Wykres poniższy przedstawia zależność n(.

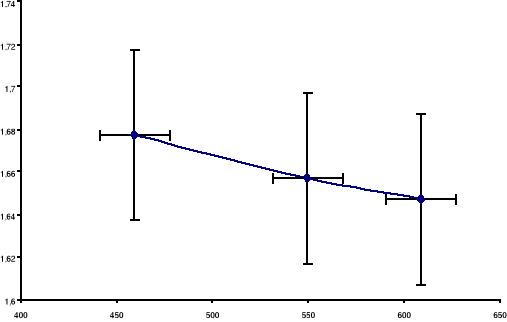
Jako  przyjmujemy wartość średnią z uzyskanych pomiarów .

Zarówno  i n obarczone są błędem, który nanosimy na wykres. Pomimo tego, że błędy na wykresie wyglądają na duże, trzeba zwrócić uwagę na skalę i na tej podstawie stwierdzimy, że wartości błędów zgadzają się z wyliczonymi i są rzędu około 5%.

---