ZADANIE 2

Obciążenia :

	Schemat I
Rodzaj obciążenia	P [kN]	Mx [kNm]	My [kNm]	Hx [kN]	Hy [kN]
CHARAKTERYSTYCZNE Stałe i zmienne długotrwałe	3000	200	400	60	-80
OBLICZENIOWE Stałe, zmienne i wyjątkowe	3600	600	600	60	100
	Schemat II
Rodzaj obciążenia	P [kN]	Mx [kNm]	My [kNm]	Hx [kN]	Hy [kN]
CHARAKTERYSTYCZNE Stałe i zmienne długotrwałe	3600	-200	-400	60	80
OBLICZENIOWE Stałe, zmienne i wyjątkowe	3950	600	-600	60	100

1. Przyjęcie liczby pali , wymiarów podstawy podpory palowej i zestawienie obciążeń.

Przyjęto :

- 6 pali Wolfsholza φ 0,40 m

- rozstaw pali r₁ = 1.35 m

- rozstaw pali r₂ = 1.40 m

- odsadzkę ( od skraju pala do skraju fundamentu) 0.20 m

Wymiary podstawy fundamentu pod słup są następujące :

L = 3.50 m B = 2.20 m h = 1.0 m

Ciężar podstawy γ_b⁽ⁿ⁾ = 24 kN/m³

- charakterystyczny

G_1n = L*B* γ_b⁽ⁿ⁾ =3.50*2.20*1.0*24 = 184.8 kN

- obliczeniowy

G_1r = 1.1* G_1n = 1.1*184.8 = 203.28 kN

Ciężar gruntu nasypowego nad fundamentem γ ⁽ⁿ⁾_Pg = 17 kN/m³

-charakterystyczny

G_2n = (L*B-a_s1*a_s2)*g₂* γ ⁽ⁿ⁾_Pg = (3.50*2.20-0.4*0.6)*0.35*17 = 44.39 kN

- obliczeniowy

G_2r = 1.2*44.39 = 53.27 kN

Ciężar posadzki betonowej

- charakterystyczny γ_b⁽ⁿ⁾ = 24 kN/m³

G_3n = (L*B-a_s1*a_s2)*g₁* γ_b⁽ⁿ⁾ = (3.50*2.20-0.4*0.6)*0.15*24 = 26.86 kN

- obliczeniowy

G_3r = 1.3*26.86 = 49.62 kN

2. Określenie położenia środka ciężkości układu palowego względem środka słupa

(założono przesunięcie e_ys , e_xs = 0)

Schemat I

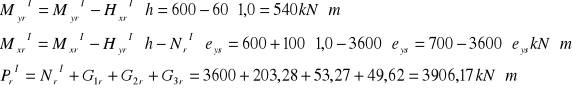
Schemat II

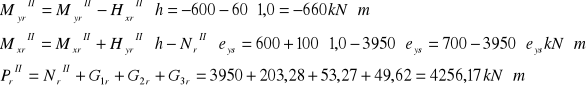
Siły w palach od wszystkich obciążeń działających na fundament

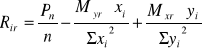
Przesunięto środek układu palowego o wartość e_ys = 0.10 m

3. Wyznaczenie sił obciążających pale.

3.1. Obciążenia stałe i zmienne długotrwałe.

Schemat I

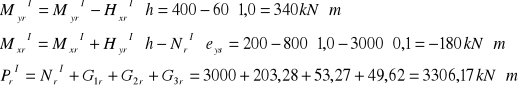
Schemat II

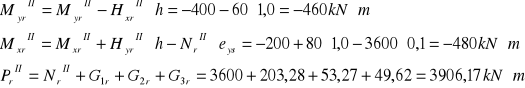
3.2. Obciążenia stałe i zmienne długotrwałe i krótkotrwałe oraz wyjątkowe.

Schemat I

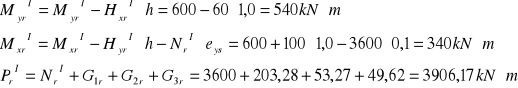
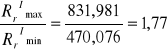
Schemat II

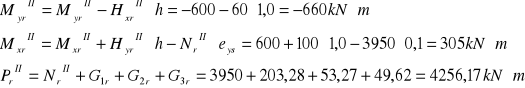
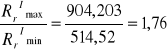
W obydwu schematach obciążeń stosunek maksymalnych sił obciążających pale do minimalnych jest mniejszy od zalecanego jako maksymalny i równego 3.

4. obliczenie długości i nośności pala.

m*Nt > Rr^Imax+Grp+Tr

Grp - ciężar własny pala

Dla pali wierconych z tab.5.7 poz.4f

S_s = 0.9 , dla piasku średniego , I_D⁽ⁿ⁾ = 0.4

S_s = 0.8 , dla gliny pylastej , I_L⁽ⁿ⁾ = 0.15

S_p = 1.0 ,

S_s = 0.9 , dla żwiru , I_D⁽ⁿ⁾ = 0.45

Pole podstawy pala (D = 0.40 m) :

Dla warstwy I poziom 0.00 znajduje się w poziomie terenu,

Dla warstwy IIIa, IIIb i IV, na poziomie określonym określonym przez h_z, ponad stropem gliny pylastej zwięzłej:

Grubość obliczeniowych warstw (h_i) , przez które przechodzi pal oraz średnie głębokości zalegania , są następujące :

I grubość 2.0 m ,średnia głębokość zalegania 2.6 m

II grubość 1.0 m ,

III grubość 1.4 m , średnia głębokość zalegania 3.23 m

IVa grubość 1.07 m , średnia głębokość zalegania 4.75 m

IVb zalega poniżej głębokości 5 m.

A. Obliczenie współczynników t_i dla średnich głębokości zalegania warstw

Warstwa I , piasek średni , I_D⁽ⁿ⁾ = 0.4 :

- dla I_D⁽ⁿ⁾ = 0.33 t = 47 kPa,

- dla I_D⁽ⁿ⁾ = 0.67 t = 74 kPa,

zatem dla I_D⁽ⁿ⁾ = 0.4

t = 47 +(74-47)*[(0.4-0.33)/(0.67-0.33)] = 52.56 kPa

- dla średniej głębokości zalegania 2.6 m

t_I = t_2.6 = 52.56*(2.6/5.0) = 27.33 kPa.

Warstwa II , torf nieskonsolidowany

- przyjęto wartość z tabeli 5.3 , przyjmuję wartość stałą tarcia niezależnie od głębokości , na całej wysokości warstwy t_II = 10 kPa.

Warstwa III , glina pylasta zwięzła , I_L⁽ⁿ⁾ = 0.15 :

- dla I_L⁽ⁿ⁾ = 0 t = 50 kPa ,

- dla I_L⁽ⁿ⁾ = 0.5 t = 25 kPa ,

zatem dla I_L⁽ⁿ⁾ = 0.15

t = 25 +(50-25)*[(0.5-0.15)/0.5] = 42.5 kPa

Dla warstwy III :

- dla średniej głębokości zalegania 3.23 m

t_IVa = t_3,23 = 42.5*(3.23/5.0) = 27.45 kPa.

Warstwa IV , żwir , I_D⁽ⁿ⁾ = 0.45 :

- dla I_D⁽ⁿ⁾ = 0.33 t = 74 kPa,

- dla I_D⁽ⁿ⁾ = 0.67 t = 110 kPa,

zatem dla I_D⁽ⁿ⁾ = 0.45

t = 74 +(110-74)*[(0.45-0.33)/(0.67-0.33)] = 86.7 kPa

Strop warstwy zalega na głębokości 3,93m poniżej poziomu zastępczego. Należy wydzielić warstwę IVa zalegającą od 3,93 - 5,0 m o miąższości 1,07 m i o średniej głębokości zalegania równej 4,75 m oraz warstwę IVb poniżej 5 m.

Dla warstwy IVa :

- dla średniej głębokości zalegania 4.75 m

t_IVa = t_4,75 = 86.7*(4.75/5.0) = 82.36 kPa.

Dla warstwy IVb :

t_IVb = t = 86.7 kPa.

B. Obliczenie współczynnika q

Średnica pala wynosi D = 0.4 m , więc głębokość krytyczna h_c= 10 m.

Wstępnie przyjęto , że podstawa pala będzie się znajdować w żwirach na głębokości większej niż 10 m poniżej poziomu zastępczego.

- dla żwiru o I_D⁽ⁿ⁾ = 0.33 q = 3000 kPa ,

- dla żwiru o I_L⁽ⁿ⁾ = 0.67 q = 5100 kPa ,

zatem dla I_D⁽ⁿ⁾ = 0.45

q = 3000+(5100-3000)*[(0.45-0.33)/(0.67-0.33)] = 3741.17 kPa

- dla poziomu podstawy (końca) pala , oznaczając przez x zagłębienie pala w żwirach poniżej poziomu 5 m , mierzonego od poziomu zastępczego :

q_x = (5+x)*(q/10) = (5+x)*( 3741.17/10) = 1870.6 +374.12*x

Powierzchnie boczne pala w obrębie poszczególnych warstw :

A_sI = 1.256*2.00 = 2.512 m²

A_sII = 1.256*1.00 = 1.256 m²

A_sIII = 1.256*1.4 = 1.758 m²

A_sIVa = 1.256*1.07 = 1.35 m²

A_sIVb = 1.256*x

C. Obliczenie wartości jednostkowych wytrzymałości q^(r) i t_i^(r)

- pod podstawą

q^(r) = 0.87*q_x = 0.87*(1870.6 +374.12*x) = 1627.42 + 325.48*x

- na pobocznicy

t_I^(r) = 1.13*27.33 =30.88 kPa

t_II^(r) = 10 kPa

t_III^(r) = 0.86*27.45 =23.61 kPa

t_IVa^(r) = 0.87*82.36 = 71.65 kPa

t_IVb^(r) = 0.87*86.7 = 75.43 kPa.

D. Wyznaczenie długości pala

l_p = ( 5.47 + x ) m.

Ciężar obliczeniowy pala (część pala poniżej z.w.g γ_b' = 24 - 10 = 14 kN/m³)

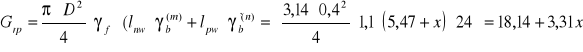
Wypadkowa negatywnego tarcia gruntu :

T_r = S_SI*A_SI*t_I^(r)+ A_SII*t_II^(r) = 0.9*2.512*30.88 +1.256*10 = 82.37 kN

Równanie , z którego wyznaczono x (zagłębienie pala ) :

m*(S_p*q^(r)*A_p+m₁*ΣS_Si*t_i^(r)*A_Si ) ≥ R_r+G_rp+T_r

założono wstępnie , że strefy naprężeń nie zachodzą na siebie (m₁ = 1)

0.9*[1.0*(1870.6 +374.12*x)*0.125+1.0*(0.8*23.61*1.758+0.9*1.35*71.65 +0.9*75.43 *1.256*x)]=

Po rozwiązaniu metodą prób otrzymano : x = 5.94 m

Obliczona długość pala l_p = 5.47 + 5.94 = 11.42 m

Przyjęto l_p = 11.5 m.

Podstawa pala będzie się znajdować na głębokości 11,5+1,6=13,1 m poniżej poziomu pierwotnego terenu.

5. Sprawdzenie nośności pala w grupie

Promień podstawy strefy naprężeń

R = (D/2)+Σh_i*tgα_i = (0.4/2)+1.4*0.070+0.105*7.1 =1.04

Osiowy rozstaw pali r = 1.35 m.

(r/R) = (1.35/1.04) = 1.30 z tab. 5.4 m₁ = 0.9

Strefy naprężeń zachodzą na siebie , nośność pala jest więc równa nośności pala pojedynczego. Przyjęta długość pala jest zatem wystarczająca.

---