![]()
, gdzie
Grupa laboratoryjna: 204 Nr ćwiczenia: 85
W skład grupy wchodzą:
Temat ćwiczenia:
Wyznaczanie górnej granicy energii promieniowania
Wydział: Ochrona Środowiska
Semestr: Drugi
Studia: Dzienne-Inżynieskie
Promieniowaniem nazywamy strumień swobodnych elektronów emitowanych przez jądra pierwiastków promieniotwórczych. Prędkość tego promieniowania zawiera się pomiędzy 0.321010 a 31010 cm/s. W powietrzu elektrony mogą przebiec drogę kilku metrów lub przeniknąć przez metalową osłonę grubości kilku milimetrów. W polu magnetycznym strumień promieniowania ugina się w tym kierunku w którym odchylają się ujemnie naładowane cząstki.
Rozróżniamy trzy rodzaje rozpadu:
Promieniowanie w wyniku emisji elektronów.
Promieniowanie w wyniku emisji pozytonów.
Wychwyt elektronów.
Promieniowanie powstaje w wyniku rozpadu promieniotwórczego jądra, z którego emitowany jest elektron, czyli cząstka , oraz antyneutrino elektronowe e, co można symbolicznie zapisać:
X Y + e + e
X jest jądrem początkowym
Y jest jądrem końcowym
Zasięg cząstek można wyznaczyć przy przejściu cząstki przez absorbent o określonej grubości. Jeśli między źródłem cząstek , a detektorem umieścimy absorbent o zmiennej grubości, to liczba cząstek przenikających przez absorbent maleje wraz ze wzrostem grubości absorbentu. dla cząstek można wyznaczyć jedynie tzw. zasięg efektywny, czyli grubość absorbentu przez który przenika mała część cząstek.
Cząstka naładowana , przechodząc przez materię oddziałuje z atomami ośrodka, przy czym oddziaływanie to może być sprężyste bądź niesprężyste. Cząstka naładowana może oddziaływać z elektronami atomu lub z jądrem co może prowadzić do reakcji jądrowych lub rozproszenia potencjalnego. Jednak prawdopodobieństwo zajścia reakcji jądrowej jest znikome. Przy rozproszeniu niesprężystym zostaje wyemitowany foton i w ten sposób zostaje wyemitowane promieniowanie hamowania.
W przypadku zderzenia cząstki z elektronem z powłoki atomowej możliwe jest wywołanie jonizacji lub wzbudzenia atomu. Prawdopodobieństwo zajścia obu tych procesów jest bardzo zbliżone oraz przez wzgląd na to, że oba te procesy dominują, promieniowanie hamowania można pominąć.
Jonizacją właściwą nazywamy liczbę par jonów wytworzonych przez cząstkę naładowaną na jednostkowej drodze w danym ośrodku. Zależy ona od rodzaju cząstki i ośrodka oraz od energii cząstki.
Zdolność hamowania ośrodka równa jest liczbowo stracie energii cząstki na jednostkowej drodze. Jest ona wprost proporcjonalna do jonizacji właściwej, a dla danego ośrodka jest tym większa im większy jest ładunek cząstki i im mniejsza jest jej prędkość.
Podczas zderzenia występują znaczne zmiany kierunku prędkości elektronów, przy jednoczesnej małej zmianie wartości prędkości. Tory elektronów są bardzo złożone i rzeczywista droga elektronów jest wielokrotnie większa od grubości absorbentu. Tak więc strumień elektronów poruszających się w danym kierunku zostaje zmniejszony przez ich zahamowanie i wychwycenie przez atomy oraz w wyniku zmiany kierunku prędkości. Istnieje maksymalna grubość absorbentu, przez który mogą przejść elektrony.
Jest to zasięg maksymalny i odpowiada cząstkom o maksymalnej energii. Na podstawie badań zależności zasięgu maksymalnego Rmax od energii maksymalnej Emax uzyskano szereg empirycznych zależności pozwalających oszacować Rmax na podstawie znajomości Emax i odwrotnie.
Liczbę elektronów wytrąconych ze strumienia I w cienkiej warstwie absorbentu o grubości dx można wyrazić równaniem: dI=Idx, gdzie - jest liniowym współczynnikiem osłabienia.
Wartość współczynnika jest wprost proporcjonalna do grubości absorbentu. W związku z tym wielkość = /, zwana masowym współczynnikiem osłabienia zmienia się bardzo wolno. Dla różnych ośrodków współczynnik absorbcji jest prawie stały, co sprawia, że dla różnych ośrodków część strumienia elektronów ulegających absorbcji i rozproszeniu jest prawie jednakowa.
dI=Idx, gdzie
= / - jest masowym współczynnikiem osłabienia [cm /g]
dx=dx - jest grubością absorbentu [g/cm ]
Po scałkowaniu powyższego równania otrzymujemy zależność:
![]()
, gdzie
I0 - jest strumieniem elektronów dochodzących do absorbentu.
Zdolność absorbcyjną ośrodka określa się często podając tzw. grubość połówkowego osłabienia x1/2
![]()
.
Jeżeli strumień cząstek wysyłany jest w półpełny kąt bryłowy to współczynnik absorbcji związany jest z Emax przybliżoną zależnością :
=0.0155(Emax )-1.44 .
Aby wyznaczyć maksymalną energię cząstek należy dokonać pomiaru liczby N cząstek, które docierają do detektora po przejściu przez absorbent o grubości x [mg/cm ] przy ustalonym czasie rejestracji t.
It=I0 t e-x
N=It - liczba cząstek zarejestrowana w czasie przy x0
N0=I0 t - liczba cząstek zarejestrowana w czasie przy x=0
Równanie to możemy zapisać inaczej:
N=N0 e-x
Wykonując pomiary zależności liczby cząstek N od grubości absorbentu x możemy wyznaczyć parametry tej prostej.
ln Nt=lnN0-Rmax
![]()
Przebieg doświadczenia.
Schemat ideowy układu pomiarowego.
D - detektor promieniowania jądrowego
Wl - wzmacniacz liniowy
P - przelicznik
ZWN - zasilacz wysokiego napięcia.
Najpierw dokonujemy pomiaru tła Nt przy czasie rejestracji t=1000 s. Następnie umieszczamy pod sondą w domku osłonowym źródło promieniowania. Dokonujemy serii pomiarów przy różnych grubościach absorbentu. Wyniki zapisujemy w tabeli 1.
Tabela 1.
Nr |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
x |
|
5.89 |
9.33 |
12.76 |
16.20 |
19.64 |
23.08 |
26.51 |
29.95 |
33.39 |
36.83 |
N |
748 |
622 |
562 |
512 |
502 |
443 |
396 |
368 |
349 |
313 |
307 |
lnN |
6.62 |
6.43 |
6.33 |
6.24 |
6.22 |
6.09 |
5.98 |
5.91 |
5.86 |
5.75 |
5.73 |
|
|
|
|
|
|
|
|
|
|
|
|
Nr |
11 |
12 |
13 |
14 |
16 |
18 |
20 |
22 |
24 |
26 |
28 |
x |
40.26 |
43.70 |
47.14 |
50.58 |
57.45 |
64.33 |
71.20 |
78.08 |
84.95 |
91.83 |
98.70 |
N |
276 |
269 |
226 |
225 |
207 |
191 |
138 |
168 |
107 |
107 |
96 |
lnN |
5.62 |
5.59 |
5.42 |
5.42 |
5.33 |
5.25 |
4.93 |
5.12 |
4.67 |
4.67 |
4.56 |
|
|
|
|
|
|
|
|
|
|
|
|
Nr |
30 |
32 |
34 |
36 |
38 |
40 |
|
|
0.017 |
|
|
x |
105.58 |
112.45 |
119.33 |
126.20 |
133.08 |
139.95 |
|
lnN0 |
6.61 |
|
|
N |
96 |
89 |
65 |
89 |
92 |
60 |
|
lnNt' |
26 |
|
|
lnN |
4.56 |
4.49 |
4.17 |
4.49 |
4.52 |
4.09 |
|
lnNt |
3.26 |
|
|
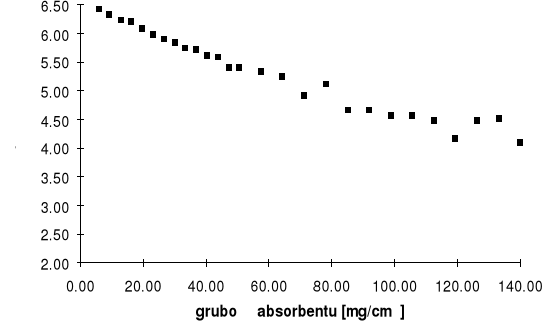
Z wykresu odczytujemy współczynnik kierunkowy prostej, który równy jest =0.017
po podstawieniu do wzoru na zasięg maksymalny otrzymujemy:
![]()
, czyli
Rmax=0.197 g/cm2
Następnie obliczamy maksymalną energię promieniowania z równania =0.0155(Emax )-1.44
![]()
![]()
![]()
E1=Emax =0.937 MeV
W tablicy odczytujemy wartość Emax w zależności od zasięgu maksymalnego i otrzymujemy, że dla
0.02<Rmax<0.3 Emax =1.92![]()
, stąd obliczamy E2=Emax =0.591 MeV
Obliczamy wartość średnią E=(E1+E2)/2
![]()
Obliczamy odchylenia od tablicowej energii Et
![]()
![]()
![]()
Ostateczne wyniki umieszczone są w poniższej tabeli
Et [MeV] |
0.765 |
[%] |
E1 [MeV] |
0.937 |
22.5 |
E2 [MeV] |
0.591 |
22.7 |
E [MeV] |
0.764 |
0.1 |
Wyznaczanie górnej granicy energii promieniowania
2