SPRAWOZDANIE Z LABORATORIUM

Z FIZYKI

TEMAT

Prawidłowości statystyczne przy rejestracji promieniowania jonizującego

INFORMATYKA GR. 5, SEKCJA 2

PLEWA ŁUKASZ

STYŁA ROBERT

ŚLOSARCZYK PRZEMYSŁAW

1.Wstęp teoretyczny.

Rozkład Poissona.

Rozkład Poissona jest rozkładem prawdopodobieństwa niezależnych zjawisk charakteryzujących się bardzo małym prawdopodobieństwem. Przykładem tego może być promieniowanie jonizujące, ponieważ źródło promieniowania zbudowane jest z pewnej ilości N atomów izotopu promieniotwórczego. Rozpad pojedynczego jądra atomu próbki nie ma wpływu na rozpad jąder innych atomów.

W przypadku rozkładu Poissona rozkład zmiennej losowej X można przedstawić w postaci:

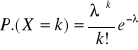
Dla rozpadu tego mamy, że :

E(X) = D²(X) = 

czyli wartość oczekiwana, wariacja i  są równe.

Wykładniczy rozkład prawdopodobieństwa

Impulsy z licznika G-M. są dobrym przykładem zdarzeń niezależnych. Odstęp czasu pomiędzy przypadkowymi zdarzeniami niezależnymi ma rozkład wykładniczy (e ^-x­). Oznacza to, ze po dowolnym impulsie następny przyjdzie najprawdopodobniej natychmiast, a długie odstępy czasu są mało prawdopodobne.

Rozkład wykładniczy jest bezpośrednio związany z rozkladem Poissona tylko wtedy, gdy odstęp miedzy impulsami podlega rozkładowi wykładniczemu. Matematycznie rozkład Poissona jest splotem rozkładów wykładniczych.

Rozkład prawdopodobieństwa typu e ^-x­ stanowi uzasadnienie przysłowia „nieszczęścia chodzą parami”. Nieszczęścia przeważnie są niezależne, dlatego najbardziej prawdopodobne jest, ze po jednym zaraz przyjdzie następne.

Rozkład równomierny

Równomierny rozkład prawdopodobieństwa nie jest związany z pomiarami radioaktywności, ma jednak zastosowanie w wielu innych zagadnieniach. Jest on ponadto bardziej prosty. Rozkład ten opisuje wynik rzutu kostka do gry kulka w ruletce. Prawdopodobieństwo każdego wyniku jest tu takie samo i co za tym idzie wynosi 1/N, gdzie N jest ilością wyniku.

2. Obliczenia i wykresy.

Z powodu ciągłych awarii urządzenia pomiarowego udało nam się dokonać tylko kilka z zaplanowanych pomiarów: przy prędkości 0,5 impulsów/s wyznaczyliśmy rozkład Poissona i rozkład wykładniczy, przy prędkości 7 impulsów/s wyznaczyliśmy rozkład Poissona. Pomiar przy prędkości 2 impulsy/s nie został uwzględniony ze względu na zbyt dużą wartość dyspersji spowodowaną awarią w czasie pomiaru.

Rozkład Poissona:

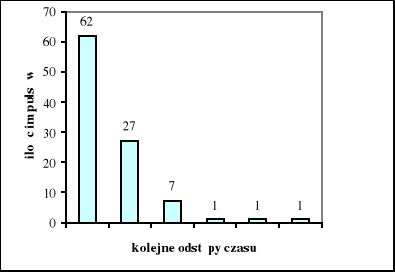
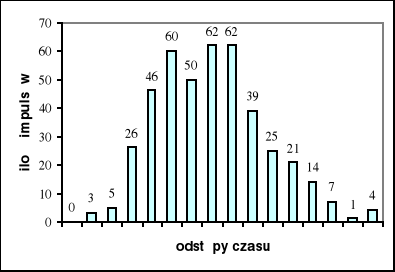
Pomiary przeprowadzone zostały dla szybkości zliczeń wynoszących 0,5 imp/s i 7 imp/s. Dla każdego z pomiarów obliczone zostały wartość oczekiwana i dyspersja. W każdym z powyższych przypadków należało sprawdzić, czy kwadrat dyspersji jest w przybliżeniu równy wartości średniej.

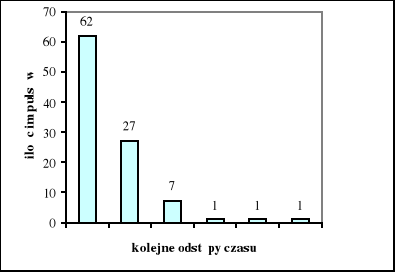
Wyniki pomiaru dla szybkości zliczeń 0,5 imp/s :

wartość średnia: 0,49495

dyspersja: 0,812828

kwadrat dyspersji: 0,66068

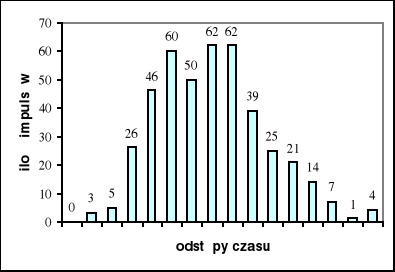
Wyniki pomiaru dla szybkości zliczeń 7imp/s :

wartość średnia: 7,0000

dyspersja: 2,7138

kwadrat dyspersji: 7,3647

W każdym z powyższych przypadków kwadrat dyspersji nie jest w przybliżeniu równy wartości oczekiwanej (choć w drugim przypadku różnica względna jest stosunkowo niewielka).

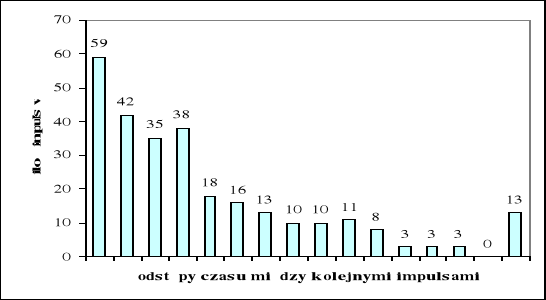
Rozkład wykładniczy

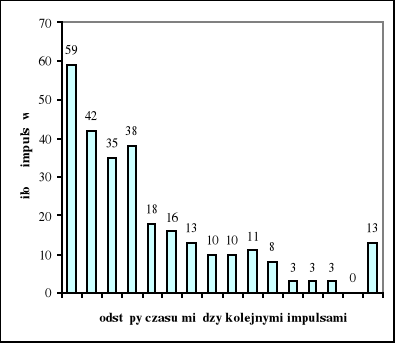
Dla prędkości 0,5 impulsów/s został przeprowadzony również rozkład wykładniczy. Pokazuje on zalezność między ilością impulsów a odstępami czasu pomiędzy wystąpieniami kolejnych impulsów. Pokazuje on, iż najbardziej prawdopodobne jest wystąpienie impulsu w krótkim czasie po poprzednim impulsie.

3.Wnioski.

Celem dwóch przeprowadzonych doświadczeń było wykazanie prawidłowości statystycznych przy zliczaniu zdarzeń niezależnych. W naszym przypadku był to opis zarejestrowania promieniowania jonizującego, który możemy opisać za pomocą rozkładu prawdopodobieństwa Poissona. Wyznaczyliśmy również rozkład wykładniczy, któremu podlegały odstępy czasu pomiędzy dwoma kolejnymi impulsami. Wykazał on, iż rzeczywiście z powodu tego, że wystąpienia impulsów są zdarzeniami niezależnymi, najbardziej prawdopodobne jest, że po wystąpieniu impulsu zaraz występuje następny (na wykresie największa liczba wystąpień jest w najkrótszych odstępach czasu).

Ponieważ przy określaniu zależności statystycznych bierzemy pod uwagę nieskończenie wiele zdarzeń, dlatego głównym powodem błędów przy określaniu badanych związków jest ograniczona liczba przeprowadzonych pomiarów.

Doświadczenie zostałoby przeprowadzone poprawniej, gdyby urządzenia pomiarowe były w pełni sprawne. Z powodu ciągłych awarii i ograniczonego czasu nie udało się przeprowadzić wyznaczenia rozkładu Poissona dla prędkości 7 impulsów/s, rozkładów wykładniczych dla prędkości 2 i 7 impulsów/s i rozkładu równomiernego.

---